---
title: 2020 年秋季 進階電腦系統理論與實作課程作業 —— dict
description: 檢驗學員對 bitwise 操作和記憶體管理的認知
---
# I04: dict
> 主講人: [jserv](http://wiki.csie.ncku.edu.tw/User/jserv) / 課程討論區: [2020 年系統軟體課程](https://www.facebook.com/groups/system.software2020/)
:mega: 返回「[進階電腦系統理論與實作](http://wiki.csie.ncku.edu.tw/sysprog/schedule)」課程進度表
## :memo: 預期目標
* 學習 [ternary search tree](https://en.wikipedia.org/wiki/Ternary_search_tree) 作為 [auto-complete](https://en.wikipedia.org/wiki/Autocomplete) 和 prefix search 的實作機制
* 學習 [Bloom filter](https://en.wikipedia.org/wiki/Bloom_filter) 和 [ternary search tree](https://en.wikipedia.org/wiki/Ternary_search_tree) 的整合議題
* bit-wise operation 的實踐
* 設計效能評比 (benchmark) 的程式框架
* 學習 GNU make 和 `Makefile` 撰寫
* 透過 Valgrind 動態程式分析工具及其模組,排除記憶體錯誤和掌握執行時期的記憶體開銷,從而更好掌握記憶體管理
* 學習 [perf](http://wiki.csie.ncku.edu.tw/embedded/perf-tutorial) 效能分析工具
:::info
:question: [Google Translate](https://translate.google.com/) 一類的線上辭典不僅能夠快速查詢詞彙,還可自動補完和提示相近詞彙,你知道背後的資料結構及數學原理嗎?
:::
## :dart: Trie 和 Ternary search tree
Binary Search Tree (BST) 查詢與建立搜尋表的時間複雜度是 O(log~2~n),但是在最糟的情況下時間複雜度可能轉為 O(n),除了要儲存的字串外不須另外分配空間。
[Trie](https://en.wikipedia.org/wiki/Trie) (亦稱 prefix-tree 或字典樹) 的時間複雜度是 O(n),能夠實現 binary search tree 難以做到的 prefix-search,缺點是需要保存大量的空指標,空間開銷較大;
[Ternary Search Tree](https://en.wikipedia.org/wiki/Ternary_search_tree) 是種 trie 資料結構,結合 trie 的時間效率和 BST 的空間效率優點。
* 每個節點 (node) 最多有三個子分支,以及一個 Key;
* Key 用來記錄 Keys 中的其中一個字元 (包括 EndOfString);
* low: 用以指向比目前節點的 Key 值小的節點;
* equal: 用來指向與目前節點的 Key 值一樣大的節點;
* high: 用來指向比目前節點的 Key 值大的節點;
Ternary Search Tree 的應用:
* spell check: Ternary Search Tree 可以當作字典來保存所有的單詞。一旦在編輯器中輸入單詞,可在 Ternary Search Tree 中並行搜尋單詞以檢查正確的拼寫方式;
* Auto-completion: 使用搜尋引擎進行時,提供自動完成(Auto-complete)功能,讓使用者更容易查詢相關資訊
對於 Web 應用程式來說,自動完成的繁重處理工作絕大部分要交給伺服器。許多時候,自動完成不適宜一下子全都下載到客戶端,TST 是保存在伺服器上,客戶端把使用者已輸入的開頭詞彙提交到伺服器進行查詢,然後伺服器依據 TST 獲取相對應的資料列表,最後把候選的資料列表返回給客戶端。
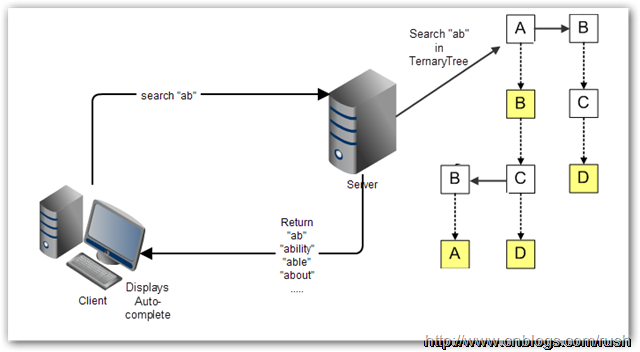
* [Autocomplete using a ternary search tree](https://github.com/jdrnd/autocomplete-ternary)
* [Ternary Search Tree 視覺化](https://www.cs.usfca.edu/~galles/visualization/TST.html)
* 以 `ab`, `abs`, `absolute` 等字串逐次輸入並觀察
* 整合案例: [Phonebook](https://github.com/raestio/Phone_book): adds new contacts and effectively search for contacts via ternary search tree
### :tangerine: Trie
[trie](https://en.wikipedia.org/wiki/Trie) 與 binary search tree 不同在於,不把整個字串包在同一個節點中 ,而是根據節點的位置決定代表的字串為何。也就是一個看結果(最終節點),一個看過程 (經過的節點)。因此利用 trie 可快速找出有相同 prefix 的字串。以下舉例示範 trie 如何儲存資料。
延伸閱讀: [字典樹 Trie](http://pisces.ck.tp.edu.tw/~peng/index.php?action=showfile&file=f743c2923f8170798f62a585257fdd8436cd73b6d)
以下逐步建構 trie:
:::info
一開始,trie tree 起始於一個空的 root: ==◎==
:::
```
◎
```
:::info
先插入一個字串 `and`
1. 首先將 and 拆解成 ==a==, ==n==, ==d==
2. 因為 a 第一次出現,所以在 root 建立一個新 children node,內含值為 a
3. 接下來從 node "a" 出發,剩下 n, d
4. n 也是第一次出現,因此在 a 建立一個新 children node,內含值為 n
5. d 比照 4 作法。
:::
```
◎
/
a
/
n
/
d
```
:::info
再插入一個字串 `ant`
1. ant 拆解成 ==a==, ==n==, ==t==,從 root 出發
2. node "a" 已經存在,因此不需要自 root 創造新的 children
3. 再來看 n,node "a" 往 children 看發現 node "n" 已存在,因此也不創造 children
4. 再來看 t 發現 n 的 children 中沒有此 node,因此創造新 children "t"
:::
```
◎
/
a
/
n
/ \
d t
```
:::info
隨後插入 ==bear==
bea 會產生像這樣子的 tree
1. 有內含數值者就是有字串存在的 node
2. 因此搜尋 "ant" 會返回 0,表示 trie 內有此字串
4. 搜尋 "be" 會返回 NULL,因為在 node "e" 無有效數值
:::
```
◎
/ \
a b
/ \
n e
/ \ \
d t a (3)
(0) (1) \
r (2)
```
以上,我們注意到 trie 中,若有儲存的字串有許多相同的 prefix ,那麼 trie 可以節省大量儲存空間,考慮到 C-style string 的設計,因為 Trie 中每個字串都是經由一個字元接著另一個字元的形式來儲存,所以具有相同 prefix 的部份都會有共同的 node。
相對的,若是資料非常大量,而且幾乎沒有相同的 prefix,將會非常浪費儲存空間。因為 trie 在記憶體的儲存方式其實是像下圖這樣,每個 node 建立時,都必須同時創造 26 個值為 NULL 的子節點。
:::success
下圖的 `universal set = { a, b, c, d, e}`,所以只創造 5 個
:::

### :taurus: Ternary search tree
Trie 能夠實現 prefix search 但會有大量空指標
- 每個 node 需要 $|alphabet set|$ 個指標
引入 [Ternary search tree](https://en.wikipedia.org/wiki/Ternary_search_tree) (TST),可望解決上述記體開銷的問題。這種樹的每個節點最多只會有 3 個 children,分別代表小於,等於,大於。在 [dict](https://github.com/sysprog21/dict) 內建的 TST 實作中的 `tst.c` 可看到資料結構如下:
```cpp
typedef struct tst_node {
char key; /* char key for node (null for node with string) */
unsigned refcnt; /* refcnt tracks occurrence of word (for delete) */
struct tst_node *lokid; /* ternary low child pointer */
struct tst_node *eqkid; /* ternary equal child pointer */
struct tst_node *hikid; /* ternary high child pointer */
} tst_node;
```
假設目前搜尋到的 prefix = x 被搜尋的 node key = cur 則
- if `x == cur`
- x = next prefix
- node = node->eqkid
- 繼續比對下個 prefix
- if `x > cur`
- node = node->hikid
- 往右搜尋
- if `x < cur`
- node = node->lokid
- 往左搜尋
而其中 `key` 為 0 時,代表 `struct tst_node *eqkid`,不是指向下個 node,而是該路徑所代表的字串。
以下範例解釋 Ternary search tree 的運作。
:::info
插入一個字串 `and`
與 trie 概念相同,但是在 root 是直接擺 ==a==,而不需要一個 null
:::
```
a
|
n
|
d
```
:::info
接著插入單字 `ant`
1. 我們先比對 ==a==,發現 a 和 root 的字母相同(a=a)
2. 因此 pointer 往下,來到 ==n== 節點,發現 n 節點和 ant 的第二個字母相同(n=n)
3. 因此 pointer 再往下,來到 d 節點,發現 d 節點和 ant 的第三個字母不同,而且 **t > d**
4. 因此 d 節點的 right child 成為 ==t==,成功將 ant 放入原本的 TST 中
:::
```
a
|
n
|
d-
|
t
```
:::info
接著插入單字 `age`
1. 我們先比對 ==a== ,發現 a 和 root 的字母相同(a=a)
2. 因此 pointer 往下,來到 n 節點,發現 n 節點和 age 的第二個字母不同,而且 **g < n**
3. 因此 n 節點的 left child 成為 ==g==,成功將 age 放入原本的 TST 中
:::
```
a
|
-n
| |
g d-
| |
e t
```
[Ternary Search Tree ](https://www.cs.usfca.edu/~galles/visualization/TST.html) 此網址提供了透過動畫呈現,展示如何加入與刪除給定字串的流程。
我們可發現 TST 幾種特性:
1. 解決 trie tree 中大量佔用記憶體的情況,因為 TST 中,每個 node 最多只會有 3 個 child
2. 但尋找時間在某些狀況中,會比 trie 慢,這是因為 **TST 插入的順序會影響比較的次數**。
考慮以下兩種插入順序:
* 前者用 `aa` $\to$ `ac` $\to$ `ae` $\to$ `af` $\to$ `ag` $\to$ `ah` 的順序
* 後者是 `af` $\to$ `ae` $\to$ `ac` $\to$ `aa` $\to$ `ag` $\to$ `ah` 的順序
試想,如果我們要尋找 `ah`,那麼前者要比較 6 次,後者只要比較 3 次。而若是建立 trie ,只需要 2 次。
- [ ] 用 `aa` $\to$ `ac` $\to$ `ae` $\to$ `af` $\to$ `ag` $\to$ `ah` 的順序插入

- [ ] 用 `af` $\to$ `ae` $\to$ `ac` $\to$`aa` $\to$ `ag` $\to$ `ah` 的順序插入

## :taurus: [ternary search tree](https://en.wikipedia.org/wiki/Ternary_search_tree) 的實作程式碼
* 取得 [dict](https://github.com/sysprog21/dict) 程式碼,編譯並測試
```shell
$ git clone https://github.com/sysprog21/dict
$ cd dict
$ make
$ ./test_common CPY
```
* 預期會得到以下執行畫面:
```
ternary_tree, loaded 259112 words in 0.151270 sec
Commands:
a add word to the tree
f find word in tree
s search words matching prefix
d delete word from the tree
q quit, freeing all data
choice:
```
* 按下 `f` 隨後按下 Enter 鍵,會得到 `find word in tree:` 的提示畫面,輸入 `Taiwan` (記得按 Enter),預期會得到以下訊息:
```
find word in tree: Taiwan
found Taiwan in 0.000002 sec.
```
* 當再次回到選單時,按下 `s` 隨後按下 Enter 鍵,會得到 `find words matching prefix (at least 1 char):` 的提示訊息,輸入 `Tain`,預期會得到以下訊息:
```
Tain - searched prefix in 0.000011 sec
suggest[0] : Tain,
suggest[1] : Tainan,
suggest[2] : Taino,
suggest[3] : Tainter
suggest[4] : Taintrux,
```
* 不難發現 prefix-search 的功能,可找出給定開頭字串對應資料庫裡頭的有效組合,你可以用 `T` 來當作輸入,可得到[世界 9 萬多個城市](https://github.com/sysprog21/dict/blob/master/cities.txt)裡頭,以 `T` 開頭的有效名稱
* 至於選單裡頭的 `a` 和 `d` 就由你去探索具體作用
上述的 `./test_common CPY` 表示 `CPY` 也就是 COPY 機制,與其相對的是 `REF`,即 reference 機制,對應的命令列為 `./test_common REF`。
程式碼中的 copy 與 reference 機制:
* copy 機制 (`CPY`): 傳入 `tst_ins_del` 的字串地址所表示的值**隨時會被覆寫**,因此 `eqkid` 需要 `malloc` 新空間將其 **copy** 存起來;
* reference 機制 (`REF`): 傳進來的字串地址所表示的值**一直屬於該字串**,以此可將其當作 **reference** 直接存起來,不用透過 `malloc` 新空間。
執行以下命令,比較 copy 與 reference 機制的效率:
```shell
$ make bench
```
參考輸出:
```
COPY mechanism
test_common => choice: find words matching prefix (at least 1 char): Tai - searched prefix in 0.000183 sec
REFERENCE mechanism
test_common => choice: find words matching prefix (at least 1 char): Tai - searched prefix in 0.000262 sec
```
預設動作是 `s Tai` (搜尋 `Tai` 開頭的字串),可改為搜尋 `T` 開頭的字串,如下:
```shell
$ make bench TEST_DATA="s T"
```
請留意以上機制的行為,後續我們會探討效能表現。
## 何謂 Bloom Filter
Bloom filter 利用 hash function,在不用走訪全部元素的前提,**預測**特定字串是否存於資料結構中。因此時間複雜度是 $O(1)$,而非傳統逐一尋訪的 $O(n)$ 。
* n-bits 的 table
* k 個 hash fucntion: h~1~ 、 h~2~ ... h~k~
* 每當要加入新字串 s 時,會將 s 透過這 k 個 hash function 各自轉換為 table index (範圍: `0` 到 `n - 1`) ,所以有 k 個 hash function ,就該有 k 個 index ,然後將該 `table[index]` 上的 bit set
* 下次若要檢查該字串 s 是否存在時,只需要再跑一次那 k 個 hash function ,並檢查是否所有的 k 個 bit 都是 set 即可

* 動畫: [Cube Drone - Bloom Filters](https://www.youtube.com/watch?v=-SuTGoFYjZs)
但這做法**存在錯誤率**,例如原本沒有在資料結構中的字串 s1 經過 hash 轉換後得出的 bit 的位置和另一個存在於資料結構中的字串 s2 經過 hash 之後的結果相同,如此一來,先前不存在的 s1 便會被認為存在,這就是 [false positive](https://en.wikipedia.org/wiki/False_positives_and_false_negatives) (指進行實用測試後,測試結果有機會不能反映出真正的面貌或狀況)。
Bloom filter 一類手法的應用很常見。例如在社群網站 Facebook,在搜尋欄鍵入名字時,能夠在 [20 億個註冊使用者](https://www.bnext.com.tw/article/45104/facebook-maus-surpasses-2-billion) (2017 年統計資料) 中很快的找到結果,甚至是根據與使用者的關聯度排序。
延伸閱讀:
* 影片: [Esoteric Data Structures and Where to Find Them](https://youtu.be/-8UZhDjgeZU?t=607)
* [Bloom Filter 影片解說](https://www.youtube.com/watch?v=bEmBh1HtYrw)
- [ ] Bloom Filter 實作方式
首先,建立一個 n bits 的 table,並將每個 bit 初始化為 0。
我們將所有的字串構成的集合 (set) 表示為 S = { x~1~, x~2~, x~3~, ... ,x~n~ },Bloom Filter 會使用 k 個不同的 hash function,每個 hash function 轉換後的範圍都是 0 到 n-1 (為了能夠對應上面建立的 n bits table)。而對每個 S 內的 element x~i~,都需要經過 k 個 hash function,一一轉換成 k 個 index。轉換過後,table 上的這 k 個 index 的值就必須設定為 `1`。
> 注意: 可能會有同一個 index 被多次設定為 `1` 的狀況
Bloom Filter 這樣的機制,存在一定的錯誤率。若今天想要找一個字串 x 在不在 S 中,這樣的資料結構只能保證某個 x~1~ 一定不在 S 中,但沒辦法 100% 確定某個 x~2~一定在 S 中。因為會有誤判 (false positive ) 的可能。
此外,**資料只能夠新增,而不能夠刪除**,試想今天有兩個字串 x~1~, x~2~ 經過某個 hash function h~i~ 轉換後的結果 h~i~(x~1~) = h~i~(x~2~),若今天要刪除 x~1~ 而把 table 中 set 的 1 改為 0,豈不是連 x~2~ 都受到影響?
- [ ] Bloom Filter 錯誤率計算
首先假設我們的所有字串集合 S 裡面有 n 個字串, hash 總共有 k 個,Bloom Filter 的 table 總共 m bits。我們會判斷一個字串存在於 S 內,是看經過轉換後的每個 bits 都被 set 了,我們就會說可能這個字串在 S 內。但試想若是其實這個字串不在 S 內,但是其他的 a b c 等等字串經過轉換後的 index ,剛好涵蓋了我們的目標字串轉換後的 index,就造成了誤判這個字串在 S 內的情況。
如上述,Bloom Filter 存有錯誤機率,程式開發應顧及回報錯誤機率給使用者,以下分析錯誤率。
當我們把 S 內的所有字串,每一個由 k 個 hash 轉換成 index 並把 `table[index]` 設為 1,而全部轉完後, table 中某個 bits 仍然是 0 的機率是 $(1-\dfrac{1}{m})^{kn}$ 。
其中 $(1-\dfrac{1}{m})$ 是每次 hash 轉換後,table 的某個 bit 仍然是 0 的機率。因為我們把 hash 轉換後到每個 index (而這個 index 會被 set) 的機率視為相等 (每人 $\dfrac{1}{m}$),所以用 1 減掉即為不會被 set 的機率。我們總共需要做 kn 次 hash,所以就得到答案$(1-\dfrac{1}{m})^{kn}$。
由 $(1-\dfrac{1}{m})^{m}≈e^{-1}$ 特性,$(1-\dfrac{1}{m})^{kn}=((1-\dfrac{1}{m})^{m})^{\frac{kn}{m}}≈(e^{-1})^{\frac{kn}{m}}≈e^{-\frac{kn}{m}}$
以上為全部的字串轉完後某個 bit 還沒有被 set 的機率。
因此誤判的機率等同於全部經由 k 個 hash 轉完後的 k bit 已經被其他人 set 的機率:
轉完後某個 bit 被 set 機率是: $1-e^{-\frac{kn}{m}}$,因此某 k bit 被 set 機率為: ==$(1-e^{-\frac{kn}{m}})^k$==
延伸閱讀:
* [Bloom Filter](https://blog.csdn.net/jiaomeng/article/details/1495500)
### 如何選參數值
* k: 多少個不同 hash
* m: table size 的大小
**如何選 k 值?**
我們必須讓錯誤率是最小值,因此必須讓 $(1-e^{-\frac{kn}{m}})^k$ 的值是最小。先把原式改寫成 $(e^{k\ ln(1-e^{-\frac{kn}{m}})})$,我們只要使 ${k\ ln(1-e^{-\frac{kn}{m}})}$ 最小,原式就是最小值。可以看出當 $e^{-\frac{kn}{m}}=\dfrac{1}{2}$ 時,會達到最小值。因此 ==$k=ln2\dfrac{m}{n}$== 即能達到最小值。
[Bloom Filter calculator](https://hur.st/bloomfilter/?n=5000&p=3&m=&k=45) 和 [Bloom Filter calculator 2](https://krisives.github.io/bloom-calculator/) 這兩個網站可以透過設定自己要的錯誤率與資料的多寡,得到 `k` 和 `m` 值。
## Bloom Filter error rate 視覺化
以 hash function的數量、table size 的大小做為橫軸縱軸,以錯誤率做為深淺。而畫面中紫色的線為 $y=ln2\cdot\frac{x}{93827}$,其中93827 為字典中 item 數量。

我們想要最小的空間及執行速度,並符合一定的錯誤率,於是期望的數值在可行域的左下角。
為了讓圖片不明顯的部分,能被看得清楚,將圖片轉為灰階後做直方圖均衡化


把此圖視為高線圖,可以發現山谷都在 $k=ln2\frac{m}{n}$上,而在這裡實際的意義就是錯誤率最小值發生在 $k=ln2\frac{m}{n}$與推導的結果相符。透過開四次方根把錯誤率之間的差距加大,再製圖,可更明顯看出上述的內容。

## 在 prefix search 導入 Bloom filter 機制
[參考的字典檔案](https://stackoverflow.com/questions/4456446/dictionary-text-file) 裡面總共有 36922 個詞彙。
經由上述運算得知,當我們容許 5% 錯誤 (=0.05) 時:
* table size = 230217
* k = 4
先用原來的 `cities.txt` 檔案做測試,以驗證估程式。
首先,這裡選用了兩種 hash function:`jenkins` 和`djb2`,另外 [murmur3 hash](https://en.wikipedia.org/wiki/MurmurHash) 也是個不錯的選擇,這裡主要是選用夠 uniform 的即可。
```cpp
unsigned int djb2(const void *_str) {
const char *str = _str;
unsigned int hash = 5381;
char c;
while ((c = *str++))
hash = ((hash << 5) + hash) + c;
return hash;
}
unsigned int jenkins(const void *_str) {
const char *key = _str;
unsigned int hash=0;
while (*key) {
hash += *key;
hash += (hash << 10);
hash ^= (hash >> 6);
key++;
}
hash += (hash << 3);
hash ^= (hash >> 11);
hash += (hash << 15);
return hash;
}
```
再來宣告我們的 Bloom filter 主體,這裡用一個結構體涵蓋以下:
* `func` 是用來把我們的 hash function 做成一個 list 串起來,使用這個方法的用意是方便擴充。若我們今天要加進第三個 hash function,只要串進 list ,後面在實做時就會走訪 list 內的所有 function。
* `bits` 是我們的 filter 主體,也就是 table 。 size 則是 table 的大小。
```cpp
typedef unsigned int (*hash_function)(const void *data);
typedef struct bloom_filter *bloom_t;
struct bloom_hash {
hash_function func;
struct bloom_hash *next;
};
struct bloom_filter {
struct bloom_hash *func;
void *bits;
size_t size;
};
```
主要的程式碼如下。
首先在 `bloom_create` 的部份,可以看到我們把兩個 hash function 透過`bloom_add_hash` 加入結構中。
再來 `bloom_add` 裡面是透過對目標字串 `item` 套用 hash ,並把 hash 產生的結果對 `filter->size` 取餘數 (第 19 行),這樣才會符合 table size 。最後第 19 行把產生的 bit 設定為 1 。
最後`bloom_test`就是去檢驗使用者輸入的 `item` 是不是在結構當中。與 add大致上都相等,只是把 bit 設定為 1 的部份改為「檢驗是不是 1」,若是任一個 bit 不是 1 ,我們就可以說這個結構裡面沒有這個字串。
這樣的實做,讓我們可以在 bloom_create 初始化完,接下來要加入字串就呼叫 bloom_add ,要檢驗字串就呼叫 bloom_test,不需要其他的操作。
```cpp=
bloom_t bloom_create(size_t size) {
bloom_t res = calloc(1, sizeof(struct bloom_filter));
res->size = size;
res->bits = malloc(size);
// 加入 hash function
bloom_add_hash(res, djb2);
bloom_add_hash(res, jenkins);
return res;
}
void bloom_add(bloom_t filter, const void *item) {
struct bloom_hash *h = filter->func;
uint8_t *bits = filter->bits;
while (h) {
unsigned int hash = h->func(item);
hash %= filter->size;
bits[hash] = 1;
h = h->next;
}
}
bool bloom_test(bloom_t filter, const void *item) {
struct bloom_hash *h = filter->func;
uint8_t *bits = filter->bits;
while (h) {
unsigned int hash = h->func(item);
hash %= filter->size;
if (!(bits[hash])) {
return false;
}
h = h->next;
}
return true;
}
```
再來是 `main` 改的部份,這裡修改 `test_common.c` 檔案。需要更動的地方是 add 和 find 功能。
首先 find 功能修改:
```cpp=
t1 = tvgetf();
// 用 bloom filter 判斷是否在 tree 內
if (bloom_test(bloom, word) == 1) {
// version1: bloom filter 偵測到在裡面就不走下去
t2 = tvgetf();
printf(" Bloomfilter found %s in %.6f sec.\n", word, t2 - t1);
printf(" Probability of false positives:%lf\n", pow(1 - exp(-(double)HashNumber / (double) ((double) TableSize /(double) idx)), HashNumber));
// version2: loom filter 偵測到在裡面,就去走 tree (防止偵測錯誤)
t1 = tvgetf();
res = tst_search(root, word);
t2 = tvgetf();
if (res)
printf(" ----------\n Tree found %s in %.6f sec.\n", (char *) res, t2 - t1);
else
printf(" ----------\n %s not found by tree.\n", word);
} else
printf(" %s not found by bloom filter.\n", word);
break;
```
由以上可見,第 3 行會先用 bloom filter 去判斷是否在結構內,若不存在的話就不用走訪。如果在的話,程式印出 bloom filter 找到的時間,以及錯誤機率,隨後走訪節點,判斷是否在 tree 裡面。
上述參數的配置為:
* TableSize = 5000000 (=五百萬)
* hashNumber = 2 (總共兩個 hash)
* 用原來的 `cities.txt` 資料量為 206849
計算出理論錯誤率約為 `0.009693`,也就是不到 `1%`。
以下是 add 的部份:
```cpp
if (bloom_test(bloom, Top) == 1) // 已被 Bloom filter 偵測存在,不要走 tree
res = NULL;
else { // 否則就走訪 tree,並加入 bloom filter
bloom_add(bloom,Top);
res = tst_ins_del(&root, &p, INS, REF);
}
t2 = tvgetf();
if (res) {
idx++;
Top += (strlen(Top) + 1);
printf(" %s - inserted in %.10f sec. (%d words in tree)\n",(char *) res, t2 - t1, idx);
} else
printf(" %s - already exists in list.\n", (char *) res);
if (argc > 1 && strcmp(argv[1], "--bench") == 0) // a for auto
goto quit;
break;
```
以上程式碼可以看到,第 1 行的部份會先偵測要加入的字串是否在結構中,若是回傳 1 表示 bloom filter 偵測在結構中,已經重複了。因此會把 res 設為 null,這樣下方第 9 行的判斷自然就不會成立。如果偵測字串不在結構中,會跑進第 3 行的 else,加入結構還有 Bloom filter 當中。
### 情境 1: 搜尋字串全部在字典內
> 以 `cities.txt` 作為輸入搜尋

從結果中可以發現:
1. tst_search 重複測試 600 次的搜尋時間大致上相同
2. 因為全部的搜尋字串都在字典內,因此 bloom filter 進行的預測時間是浪費的,隨著 table size、雜湊函式數量提高,浪費的時間愈多
### 情境 2: 搜尋字串在第一個字元即可判斷不在字典內

1. 加上 bloom filter 後的執行時間為 L 型:
在這個情境中,若 bloom filter 預測錯誤,進行一個搜尋所花的時間為 bloom filter + tst_search 的時間;若是預測正確則是只需要花 bloom filter 的時間,因此預測的錯誤率愈低搜尋所需要的時間愈短。
已知: ==bloom filter 預測的錯誤率計算公式為 $(1-e^{-\frac{kn}{m}})^k$==
**其中 k為 hash function 數量、m 為 table size、n 為字串數量**
依據上述公式,當 k 固定時,m 增加錯誤率會逐漸下降,繪製出的圖形也是呈現 L 形與輸出結果相符。
2. 把這張圖 bloom filter 的部分與 bloom filter錯誤率的 heat map 一起看,由於錯誤率與執行時間成正比,這張圖 bloom filter 的部分,正是一列一列拆開的 heat map。
3. 因為在第一個字元就可以判斷出字串不在字典中,tst_search 進行搜尋的時間反而少於進行 hash 的時間。
### 情境 3: 搜尋到最後一個字元才發現字串不在字典內

1. 第三個 L 之後加入 bloom filter 的搜尋時間全在不加 bloom filter 之上,這與==搜尋的字串長度==有關,雖然搜尋字串全部不在字典中且需要到最後一個字元才能發現,但因為字串長度不長,當雜湊函式的數量大於 3 個之後,進行雜湊運算與預測的時間反而大於 tst_search,因此在輸入的搜尋字串長度與本次情境相近時,bloom filter 的雜湊函式數量小於 3 個才可以使效率提高。
## Bloom filter 空間浪費改善
原本整個 table 都把 byte 當 bit 來用,浪費 $\dfrac{7}{8}$ 的 table 空間
```cpp
void bloom_add(bloom_t filter, const void *item) {
struct bloom_hash *h = filter->func;
uint8_t *bits = filter->bits;
while (h) {
unsigned int hash = h->func(item);
hash %= filter->size;
bits[hash] = 1; // 每個 uint8_t 不是 1 就是 0
h = h->next;
}
}
```
做以下改善:
```cpp
bloom_t bloom_create(size_t size)
{
bloom_t res = calloc(1, sizeof(struct bloom_filter));
res->size = size;
//res->bits = malloc(size + 7);
res->bits = calloc((size + 7) >> 3, 1);
bloom_add_hash(res, djb2);
bloom_add_hash(res, jenkins);
return res;
}
```
為了改善空間浪費,在 `bloom_create` 內做以上更改
- 因為從 byte-level 改成 bit-level 所以 res->bits 只需要 malloc 1/8 的空間
- 其中 `res->bits = calloc((size + 7) >> 3, 1)` 先對齊 1-byte (round up) 再 shift 3 bits
- 這邊不用 `(size + 7) & -8` 因為會 shift 掉
- `res->bits = calloc((size + 7) >> 3, 1)` 改成 `calloc` 因為要確保原本 memory content 為 0
```cpp
void bloom_add(bloom_t filter, const void *item)
{
struct bloom_hash *h = filter->func;
uint8_t *bits = filter->bits;
while (h) {
unsigned int hash = h->func(item);
hash %= filter->size;
//bits[hash] = 1;
bits[hash >> 3] |= 0x40 >> (hash & 7);
h = h->next;
}
}
```
```cpp
bool bloom_test(bloom_t filter, const void *item)
{
struct bloom_hash *h = filter->func;
uint8_t *bits = filter->bits;
while (h) {
unsigned int hash = h->func(item);
hash %= filter->size;
if (!(bits[hash >> 3] & (0x40 >> (hash & 7)))) {
return false;
}
h = h->next;
}
return true;
}
```
在以上二個函式中,因為 table 的儲存已經改成 bit-level 所以
- `bits[hash >> 3]` 先找到存放位置在第幾個 byte
- `0x40 >> (hash & 7)` 再找到要放在第幾個 bit
- 在 little-endian 往右 shift 會往低位址移動,但是不影響結果
- 也可寫成 `1 << (hash & 7)`,只是前者邏輯上較直觀
### 分飾多角的 eqkid
資料結構:
```cpp
typedef struct tst_node {
char key; /* char key for node (null for node with string) */
unsigned refcnt; /* refcnt tracks occurrence of word (for delete) */
struct tst_node *lokid; /* ternary low child pointer */
struct tst_node *eqkid; /* ternary equal child pointer */ /** 其實它分飾多角 **/
struct tst_node *hikid; /* ternary high child pointer */
} tst_node;
```
`tst_ins_del` 實作:
```cpp
void *tst_ins_del(tst_node **root, const char *s, const int del, const int cpy)
{
...
while ((curr = *pcurr)) { /* iterate to insertion node */
...
return (void *) curr->eqkid; /* pointer to word */
...
pcurr = &(curr->eqkid); /* get next eqkid pointer address */
...
}
for (;;) {
...
curr->eqkid = (tst_node *) s;
return (void *) s;
...
}
}
```
乍看之下一頭霧水,為何有時將 `eqkid` 傳出去當 word 起始位置,有時又用它來取得下個 node,有時將傳進來的 `const char *s` 轉型成 `tst_node *` 呢?其實從 `tst_suggest` 可以看出些端倪:
```cpp
void tst_suggest( ... )
{
...
if (p->key)
tst_suggest(p->eqkid, c, nchr, a, n, max);
else if (*(((char *) p->eqkid) + nchr - 1) == c)
a[(*n)++] = (char *) p->eqkid;
...
}
```
若 `key` 非 0(`key` 爲 0 的 node 的存在是爲了表示 parent node 的結尾),則將 `eqkid` 當 node 指標進行 recursive call,否則當作字串使用。
這裡需要記錄字串是因爲走訪到 node 之後要得知該 node 代表的字串是有點麻煩的事情(若有記錄 parent,可以往上透過一些規則找回),但這裡很巧妙的利用了 `eqkid` 當作 `char *` 指向該 node 表示的字串。
關於程式碼的 copy (`CPY`) 與 reference (`REF`) 機制,前者是傳入 `tst_ins_del` 的字串地址所表示的值**隨時會被覆寫**,因此 `eqkid` 需要 `malloc` 新空間將其 **copy** 存起來,而後者是傳進來的字串地址所表示的值**一直屬於該字串**,以此可將其當作 **reference** 直接存起來,不用 `malloc` 新空間。
承接上面,`eqkid` 分飾多角,沒有需要重複使用的時候嗎?
|Insert XY|Insert XYZ|Insert XY and XYZ
|--|--|--|
|  |  |  |
如上面第三種情況,node Z 的 `eqkid` 該指向 ``"XY"`` 表示該字串結束,還是指向下一個 `key` 爲 0 的 node 表示 `"XYZ"` 的結束呢?
再仔細觀察及思考會發現 node Z 的 key 爲 `'z'`,已無法表示字串 `"XY"` 的結束,`tst_node` 中也沒有類似綠色的屬性,所以 tst.c 的實作實際上是這樣的:
|Insert XY and XYZ in order|Insert XYZ and XY in order|
|--|--|
|||
> 注意:上圖(兩張都)請將 N 當作小綠空圓(表示字串 `"XY"` 的結束)並無視它下面的小綠空圓,而左圖 `>N` 爲 `>0`
可見用來表示結束的 node 永遠不會有 ternary equal child, 因此 `eqkid` 就不會分身乏術。
## 資料檔案的分析
檔案 `cities.txt` 提供超過 9 萬筆城市和所屬的國家/地區。城市名後面跟着逗號 (`,`),由於國情和文化落差,我們務必要留意到這些城市的命名行為及特例。我們可運用 [regular expression](https://en.wikipedia.org/wiki/Regular_expression) 來分析。
* Pattern `,(.*)?,(.*)?,(.*)?,`: 有 4 個逗號的資料,共有 1 個結果
> 命令: `$ egrep ",(.*)?,(.*)?,(.*)?," cities.txt`
* `Villa Presidente Frei, Ñuñoa, Santiago, Chile, Chile`, 依序為 `建築物名稱, 城鎮名, 城市名, 國名`。其中城市名的部份為 `Santiago, Chile`,後者為 "Santiago de Chile" 的縮寫
* Pattern `,(.*)?,(.*)?,`: 有 3 個逗號的資料,共有 3 個結果
> 命令: `$ egrep ",(.*)?,(.*)?," cities.txt`
* `Oliver-Valdefierro, Oliver, Valdefierro, Spain`, 依序為 `城市名, 區名, 區名, 國名`。 其中 Oliver 和 Valdefierro 是兩個相同層級的行政區
* `Earth, TX, Texas, United States`, 依序為 `城市名, 州名縮寫, 州名, 國名`。這是例外,因為除此之外的所有美國的地名都是遵循 `城市名, 州名, 國名` 的格式。
* Pattern `,(.*)?,`: 有 2 個逗號的資料,共有 19191 個結果
> 命令: `$ egrep ",(.*)?," cities.txt`
* 大部份為美國、加拿大、墨西哥、澳洲等有州層級的行政區規劃的國家,可粗略推測這種情況的資料,中間的部份都是州
* 剩下的就是只有一個逗號的國家,格式為 `城市名, 國名`
為了解析的便利,我們可將上述有三個以上逗號的資料取代如下:
* `Villa Presidente Frei, Ñuñoa, Santiago, Chile, Chile` $\to$ `Ñuñoa, Chile`
* 因為智利其他的地名都是遵循 `城市名, 國名` 的格式,而且 `Santiago, Chile` 已存在
* `Oliver-Valdefierro, Oliver, Valdefierro, Spain` $\to$ `Oliver-Valdefierro, Spain`
* 因為就西班牙的行政區分類,這兩個地名本來就被視為是[同一個區](https://es.wikipedia.org/wiki/Oliver-Valdefierro),且大部份西班牙的地名都是遵循 `城市名, 國名` 的格式
* `Earth, TX, Texas, United States` -> `Earth, Texas, United States`
* 除此之外,所有美國的地名都是遵循 `城市名, 州名, 國名` 的格式
還有個例外是 `Xeraco,Jaraco, Spain`,該城市名的逗號後方沒有空白鍵(僅此一筆例外)。這因 Xeraco 和 Jaraco 實際指同一個地方,只是拼法不同,因此保留西班牙本地常用的 Xeraco 即可。
如此一來,這份資料就只剩下「有一個逗號的資料」跟「有兩個逗號的資料」了,在我們假設「有兩個逗號的資料」都是`城市名, 州名/省名, 國名`的情況下,我們可以用以下程式碼讀取輸入(此方法會將逗號和換行符都排除):
```cpp
char line[WRDMAX];
while (fgets(line, WRDMAX, fp) != NULL) {
char city[WRDMAX] = "", province[WRDMAX] = "", nation[WRDMAX] = "";
sscanf(line, "%[^,^\n], %[^,^\n], %[^,^\n]", city, province, nation);
/* Do what you want */
}
```
## 使用 perf 分析程式效能
Perf 全名是 Performance Event,是在 Linux 2.6.31 以後內建的系統效能分析工具,它隨著核心一併釋出。藉由 perf,應用程式可以利用 PMU (Performance Monitoring Unit), tracepoint 和核心內部的特殊計數器 (counter) 來進行統計,另外還能同時分析運行中的核心程式碼,從而更全面了解應用程式中的效能瓶頸。
參考 [使用 perf_events 分析程式效能](https://zh-blog.logan.tw/2019/07/10/analyze-program-performance-with-perf-events/) 和 [簡介 perf_events 與 Call Graph](https://zh-blog.logan.tw/2019/10/06/intro-to-perf-events-and-call-graph/) 這兩份中文介紹,事先安裝好 `perf` 並熟悉其使用方式。
* ==在自己的 Linux 開發環境實際操作==
* 再次提醒:你的 GNU/Linux「==不能==」也「==不該==」透過虛擬機器 (如 VMware, VirtualBox, QEMU 等等) 安裝
* 請務必依據 [GNU/Linux 開發工具共筆](https://hackmd.io/@sysprog/gnu-linux-dev/) 指示,將 Linux 安裝於實體硬碟並設定好多重開機
CPY 機制在 prefix-search 時效率較好的原因,可見 `tst.c` 的 `tst_ins_del`:
```cpp
void *tst_ins_del(tst_node **root, const char *s, const int del, const int cpy)
{
...
if (*p++ == 0) {
if (cpy) { /* allocate storage for 's' */
const char *eqdata = strdup(s);
if (!eqdata)
return NULL;
curr->eqkid = (tst_node *) eqdata;
return (void *) eqdata;
} else { /* save pointer to 's' (allocated elsewhere) */
curr->eqkid = (tst_node *) s;
return (void *) s;
}
}
...
}
```
CPY 機制在 insert 時,建立 leaf 後會間接呼叫 `malloc` 來保存字串,在這之前的最後一次 `malloc` 是爲了配置該 leaf 的空間。一直 `malloc` 時,heap 也會形同 stack 一般地增長,所以像給定測試條件很規律的狀況下,字串地址與 leaf 的地址很可能都很靠近。
換言之,CPY 機制在一開始`p->eqkid` 後,字串就很大可能在 cache 裡面了,因此 cache miss 機率較低,這就是它相對來說在 prefix-search 上效率比較好的原因。
CPY 機制與 REF 機制在建 tree 的效率比較
+ CPY 機制
+ 讀檔時每次將地名暫時存入同一字串 `word`
:+1: 只要 cache 沒被覆蓋就不會發生 cache miss
+ ternary search tree 的 terminal node 用 `strdup` 將地名存起來
:-1: 需要複製字串(影響小)
:-1: 間接呼叫 `malloc`,可能涉及大量系統呼叫
+ REF 機制
+ 讀檔時每次將地名永久(直到 memory pool 被 free)依序存入 memory pool
:-1: cache miss 次數 $\ge$ 使用的 memory pool 大小 / cache 一次載入的大小
+ ternary search tree 的 terminal node 直接存 reference(指向 memory pool 的某個位置)
:+1: 沒有明顯額外 overhead
## :penguin: 作業要求
* 在 GitHub 上 fork [dict](https://github.com/sysprog21/dict),視覺化 ternary search tree + bloom filter 的效能表現並分析。注意,需要設計實驗,允許不同的字串輸入並探討 TST 回應的統計分佈
* :warning: 若你的 GitHub 帳號在 2020 年 9 月 24 日已自 [dict](https://github.com/sysprog21/dict) fork,請在 GitHub 上重新 fork
* 要考慮到 prefix search 的特性還有詞彙的涵蓋率
* 限用 gnuplot 來製圖
* 以 perf 分析 TST 程式碼的執行時期行為並且充分解讀
* 考慮到 CPY 和 REF 這兩種實作機制,思考效能落差的緣故,並且提出後續效能改善機制
* 充分量化並以現代處理器架構的行為解讀
* 如何兼顧執行時間和空間運用效率?
* 研讀 [Xor Filters: Faster and Smaller Than Bloom and Cuckoo Filters](https://arxiv.org/abs/1912.08258) 論文並參閱對應程式碼實作 [xor_singleheader](https://github.com/FastFilter/xor_singleheader),引入上述 [dict](https://github.com/sysprog21/dict) 程式碼中,需要比較原有的 bloom filter 和 xor filter 在錯誤率及記憶體開銷
* 善用 Valgrind 和 [Massif](https://valgrind.org/docs/manual/ms-manual.html),使用方式參見 [I01: lab0](https://hackmd.io/@sysprog/2020-lab0)
* 如何縮減頻繁 malloc 帶來的效能衝擊呢?提示: [memory pool](https://en.wikipedia.org/wiki/Memory_pool)
* 儲存字串用的 memory pool 在 REF 版本中已實作,但在 `tst_ins_del()` 當中頻繁以 calloc() 配置節點空間造成的效能衝擊,應許以改進。
* REF 版本中的 pool 只會一直增添新的資料,並沒有從中移除資料的操作發生,因此可以用更進階的手段來管理
* tst 則會有移除節點的操作,我們無法確定要被刪除的節點他使用的記憶體落在 memory pool 的哪個地方,如何管理 memory pool, 使之不會有記憶體碎片產生,是這個問題的關鍵。
* 在現有的開放原始碼專案中,找出使用 bloom filter 的專案,並解析其導入的考量
## 繳交方式
* 編輯 [Homework 3 作業區共筆](https://hackmd.io/@sysprog/2020-homework3),將你的觀察、上述要求的解說、應用場合探討,以及各式效能改善過程,善用 gnuplot 製圖,紀錄於新建立的共筆
## 截止日期
* Oct 7, 2020 (含) 之前進行,不該截止日前一天才動手
* 越早在 GitHub 上有動態、越早接受 code review,評分越高
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet