# Sin7Y Tech Review (18): Zero-Knowledge Proof Algorithm: ZK-Stark---FRI Protocol
## Preface
Finally, we reach the conclusion of the series "Understanding the value of a zero-knowledge proof algorithm - Zk-stark". We discussed the overall structure of the Zk-stark algorithm, the first part of the algorithm, Arithmetization, and the second part of the algorithm, Low Degree Testing, in the previous three articles. I believe that after reading these articles, you will have a general understanding of the outline of the Zk-stark algorithm. However, you may question the accuracy of some sentences or illustrations in the article. Indeed, a more specific introduction and explanation are required for certain contents. Otherwise, misunderstandings may occur.

In the third article, we have discussed the importance of conducting LDT on polynomials to ensure that the values returned by the prover satisfy the equality of polynomial equations are indeed calculated using effective polynomials. In the meantime, to minimize the complexity of the verifier, we have transformed the original polynomial and thus the polynomial to be verified by the verifier is only half the original polynomial. Repeat until the degree of the polynomial can be determined directly. This is the fundamental concept of the FRI protocol. Now, let us go over the FRI protocol in detail.

## FRI Protocol
FRI, *Fast RS IOPP*, or *Fast Reed---Solomon Interactive Oracle Proofs of Proximity*, is a more effective proximity test method that is used to determine whether a set of points is mostly on a polynomial with a degree less than a specified value and can achieve linear proof complexity and logarithmic verification complexity or not. Before we introduce the FRI protocol in its entirety, let us consider a simple scenario.

There exists a multiplicative group $L_{0}$ of order $2^{n}$ on a Galois Field $F$.

* At this point, the prover asserts that the codeword $f_{0}: L_{0} ->\mathbf{F}$ satisfies the $R S\left[F, L_{0}, \rho\right]$ coding parameter, that is, the majority of the points in $f_{0}$ lie on a polynomial $P (x)$ of order ; here $\rho=2^{(-R)}$;

As a result, when $f_{0}=P$, there exist polynomials $\operatorname{deg}\left(P_{1}, P_{2}\right)<1 / 2 * \rho * 2^{n}$ whose order satisfy the relationship of and satisfy the following equation:

$f_{0}(x)=P(x)=P_{1}\left(x^{2}\right)+x * P_{2}\left(x^{2}\right) (1)$

Set $Q(x,y)=P_{1}(y)+x*P_{2}(y)$ we can see the order $d<2$ of binary polynomial $Q(x, y)$ concerning for variable $x$; The order $d<1 / 2 * \rho * 2^{n}$. of variable $y$, and when $y=x^{2}$, there is $Q(x, y)=f_{0}(x)$; At this time, the verifier $V$ randomly selects a value $x_{0}$ and sends it to the prover $P$. The prover $P$ calculates $Q\left(x_{0}, y\right)$ and sets:

$f_{1}(y)=Q\left(x_{0}, y\right)=P_{1}(y)+x_{0} * P_{2}(y) (2)$

For polynomial $f_{1}(y)$, since $y=x^{2}$ and $x$ has a value range of the Group $\mathbf{L}_{0}$, thus there is the equation $x^{\left(2^{n}\right)}=1$, which can be further converted to $\left(x^{2}\right)^{n}=1$. Therefore, if the value range of the independent variable $y$ is defined as the Group $L_{1}$, then $L_{1}$ should have the following properties:

* The order of the group is $2^{(n-1)}$;
* Each element of the Group $L_{1}$ corresponds to two elements of the Group $L_{0}$; that is, for any element $y$ of the Group $L_{1}$, there are two elements $x$ and $(-x) \bmod p$ in the Group $L_{0}$, which satisfies $x^{2} \bmod p=y \& \&(-x)^{2} \bmod p=y_{;}$

So far, the issue is transformed into the one in which the prover $P$ shall prove whether the order of polynomial $f_{1}(y)$ satisfies $d<1 / 2 * \rho * 2^{n}$ or not; at the same time, the consistency of function $f_{1}$ and $f_{0}$ shall be ensured. Specific steps are as follows:

* The verifier $V$ selects three points $y, s_{0}, s_{1}$ from the Group $L_{1}$ and the Group $L_{0}$ to satisfy $s 0 !=s 1 \& \& s_{0}^{2}=s_{1}^{2}=y$
* The prover $P$ returns three values of $f_{0}\left(s_{0}\right), f_{0}\left(s_{1}\right), f_{1}(y)$.
* The verifier $V$ interpolates a polynomial $g(x)$ of order $d<2$ according to $f_{0}\left(s_{0}\right), f_{0}\left(s_{1}\right)$.
* Verifier $V$ verifies $g\left(s_{0}\right)=f_{1}(y)$, and if not equal, the verification fails.
* //2022-01-11 Error description $g\left(x^{0}\right)=f_{1}(y)$ was modified.

**Reliability analysis:** if the function $f_{1}$ is not converted from the function $f_{0}$ according to the above process, then it is in large probability that the polynomial $P_{1}\left(x^{2}\right)$ and $P_{2}\left(x^{2}\right)$ of formula (1) and the polynomial $P_{1}(y)$ and $P_{2}(y)$ of formula (2) are not equal to each other. Considering that the order of the polynomial satisfies $d<1 / 2 * \rho * 2^{n}$, and the value range of the variable is $2^{(n-1)}$, the probability of equality of the polynomial is $\frac{1 / 2 * \rho * 2^{n}}{2^{(n-1)}}=\rho$ if a value is randomly selected within this range according to Schwartz Zippel theorem. $\rho$ represents coderates. If $\rho=2^{-8}$, then the probability of successful verification for just one time is merely $2^{-8}$. If it is verified for $\mathrm{k}$ times, the probability of success in operating with bad manners is equal to $2^{-8 \mathrm{k}}$. With the increase of the value of $k$, the probability is infinitely close to 0 .

Repeat the above process for the function $f_{1}$ until the polynomial $f_{r}$ becomes a form that can effectively judge the order, and the whole LDT process is completed.

Next, let's take a look at the specific contents of the FRI protocol, as shown in Figure 1:

FRI protocol is divided into two stages: $commit$ and $query$. As can be seen from the previous simple scenario example, an interaction process requires:
1. The verifier $V$ sends the random number $x_{0}$ to the prover $P$;
2. The prover $P$ generates a new polynomial $f_{i}$
3. The verifier $V$ generates the point sets $s_{0, i}, s_{1, i}, y_{i}$ of queries and sends them to the prover $P$
4. The prover $P$ calculates the corresponding polynomial values of $f_{i}\left(y_{i}\right), f_{i-1}\left(s_{0, i}\right), f_{i-1}\left(s_{1, i}\right)$
5. The verifier $V$ conducts a validity check.

Next, we'll introduce the meaning of parameters and steps in $Commit$ and $Query$ protocols and then summarize the relevant processes.

$Commit$:

**Common input**

* $R$ : coding ratio parameter
* $i$ : number of cycle times index
* $r${: cycle times, value ${\frac{k_{0}-R}{\eta}}$
* $\eta$ : spatial mapping parameter $x=>x^{2^{\eta}}$
* Order of $\mathrm{L}_{0}: 2^{k_{0}}$
* $R S\left[F, L_{i}, \rho\right]$ : Encoding parameters [Galois Field, scope field, encoding ratio]
* $q_{0}(x)=x^{2^{\eta}}, L_{i+1}=q_{0}\left(L_{i}\right), \quad$ Represent the mapping from the Group $L_{i}$ to the Group $L_{i+1}$

**Prover input**

* $f_{i}$ represents the function input of the cycle by the $i$ time
* $L_{i}$ represents the group corresponding to the cycle by the $i$ time, with the order of $2^{n-i}$
* $R S_{i}$ : Coding parameters corresponding to $f_{i}$

**LOOP $i \leq r$**

1.

* $x_{i}$ : The random number sent by the verifier $V$

2.

* $S_{y}$ : Each element of the Group $L_{i+1}$ corresponding to the element set of the Group $L_{i}$
* $P_{y}^{i}(X)$ : Polynomial interpolated based on the value of $f_{i}(x)$ on $S_{y}$
* $f_{i+1}(y)==P_{y}^{i}\left(x_{i}\right):$ Indicating the consistency between polynomials $f_{i+1}$ : and $f_{i}$.

3. $i==r$

* Generating polynomial $\quad f_{r}$
* Interpolate a polynomial $P^{r}(x)$
* Calculate the order of a polynomial $P^{r}(x)$
* Save coefficients $a_{0}, \ldots, a_{d}$ of a polynomial $P^{r}(x)$
* End of Commit stage

4. $\mathrm{i}<\mathrm{r}$

* Generate $f_{i+1}$ according to the calculation method in step 2
* Calculating commitment to polynomials $f_{i+1}$
* Update relevant parameters and enter the next cycle

$Query$:

**Verifier input**

* See Commit for $R / \eta / L_{i} / R S_{i} / x_{i} / f_{i} / P(x)$
* $l:$ query times, repeated multiple times to reach the required security level$

**Reconstruct $f_{r}$**

* Access oracle to obtain $a_{0}, \ldots, a_{d}$, and reconstruct polynomial $P^{r}(x)$
* Calculate all values of $P^{r}(x)$ on the Group $L_{r}$ and assign values to $f_{r}$

**Repeat $l$ times**

* $\mathrm{i}=\{0 \sim \mathrm{r}-1\}$

$S_{i}$ satisfies the set of $s_{i}$ in $s_{i+1}=q_{0}\left(s_{i}\right)$

For example, starting from the Group $L_{0}$, randomly select an element $s_{0}$ and calculate $s_{1}=q_{0}\left(s_{0}\right)$, then $s_{1}$ is the element of the Group $L_{1}$. However, there is also $-s_{0}$ (assuming $q_{0}(x)=x^{2}$ ) satisfying the above relationship on the Group $L_{0}$, so there is $S_{0}=\left\{s_{0},-s_{0}\right\}$; Similarly, continue to repeat the above calculations with $s_{1}$ for $\mathrm{r}$ times, and a series of sets of $S_{0}, S_{1}, \ldots, S_{r-1}$ will be obtained.

* $\mathrm{i}=\{0 \sim \mathrm{r}-1\}$

On the set of $S_{0}, S_{1}, \ldots, S_{r-1}$ obtained in step 1, respectively QUERY the value of polynomial $f_{i}$

Verify that the returned value is consistent with the corresponding polynomial commitment (if the commitment in the COMMIT stage is the merkle-based hash calculation, then here multiple hash calculations are required to obtain the root)

Interpolate $P_{0}(x), P_{1}(x), \ldots, P_{r-1}(x)$ in turn

* round consistency check $\mathrm{i}=\{0 \sim-1\}$

Verify $f_{i+1}\left(s_{i+1}\right)=P_{i}\left(x_{i}\right)$ in sequence

* If all verifications are successful, the verification passes.

Next, set $\eta=1$ (i.e. $q_{0}(x)=x^{2}$ ) as an example to describe the two-stage process of FRI protocol, as shown in the following figure: $d<\rho * 2^{n}$


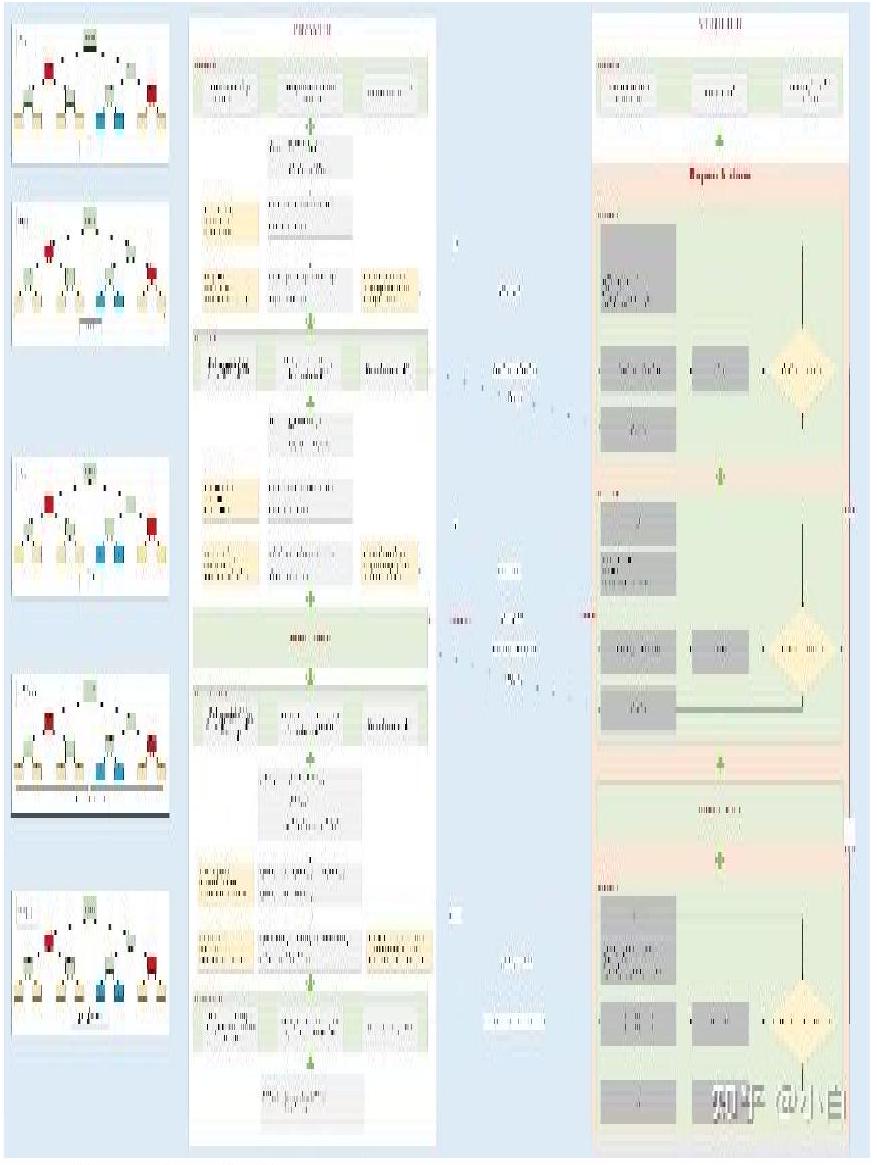
As can be seen from the above process:

* For the consistency check of each round, it is ensured that the original polynomial $f_{0}$ does satisfy the order $d<\rho * 2^{n}$ .
* If the above protocol is repeated for $l$ times, the probability of success of the people operating with bad manners can be greatly reduced.

## Summary
The process described above is the FRI protocol. As can be seen, the complexity of the verification satisfies the logarithmic relationship . The algorithm ensures that the round consistency verifications can be passed if and only if the initial polynomial satisfies . The actual implementation may vary slightly. For more information, please refer to the DEEP-FRI paper. In comparison to FRI, DEEP-FRI increases the system’s reliability while maintaining an optimal level of proof and verification complexity.

Based on the previous three articles in this series, the Zk-STARK algorithm can be summarized as follows:
1. The algorithm is divided into two parts: Arithmeticalization and LDT
2. Arithmeticalization converts the issue to polynomial equality and polynomial LDT issue.
3. The FRI protocol is used in the LDT stage to ensure the complexity of linear proof and the complexity of logarithmic verification
4. The zero-knowledge attribute ensures that the verifier cannot access the points in the trajectory polynomial and that the trajectory polynomial contains privacy values.
5. Simultaneously, to ensure the zero-knowledge attribute, random values for rows must be added to the trajectory polynomial, which is determined by the verifier and prover after negotiation.
6. CRS is not required as a third party throughout the process.
7. The entire process does not depend on any mathematical problems.

## Appendix
1. [Official Brief Introduction of FRI](https://medium.com/starkware/low-degree-testing-f7614f5172db)
2. [FRI Paper](https://eccc.weizmann.ac.il/report/2017/134/)
3. [DEEP-FRI Paper](chrome-extension://cdonnmffkdaoajfknoeeecmchibpmkmg/assets/pdf/web/viewer.html?file=https%3A%2F%2Farxiv.org%2Fpdf%2F1903.12243.pdf)
5. [Reed-Solomen WIKI]( https://en.wikipedia.org/wiki/R)