Taiko L2 EIP-1559

The overall design

The EIP-1559 base fee per gas (basefee) on Taiko L2 is calculated by Taiko L1 protocol contracts and injected into the block's metadata. The Taiko client should skip calculating the basefee value, and stop burning the basefee, and send it to a named address ("treasury") specified in Taiko L1 protocol contracts, which will be verified by Taiko ZKP.

Basefee Calculation

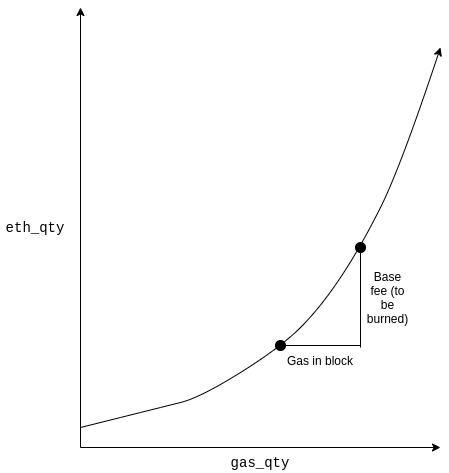
We use Vitalik's idea proposed here: https://ethresear.ch/t/make-eip-1559-more-like-an-amm-curve/9082 (read it first!). The x-axis represents the current gas excess, the y-axis is the ether amount. When some gas are sold, excess goes up, and the difference of the new and the old y value is the total cost of the gas purchase, or

$$cost(gasAmount)=e^{(gasExcess+gasAmount)}-e^{gasExcess}$$, and

$$basefee(gasAmount)=cost(gasAmount)/gasAmount$$.

A nice property of the

$e^x$ curve is that for a chosen gas target

$T$, the basefee (

$basefee(T)$) for a block with

$T$ gas and the basefee (

$basefee(2T)$) for a block with

$2T$ gas always have the fixed ratio:

$$R==basefee(2T)/basefee(T)$$ regardless of the current gas excess value,

$T$ and

$R$ together determine the shape of the curve. In Ethereum,

$T$ is 15 million and

$R$ is 12.5%; it's yet to be decided what value we should use in Taiko.

Implementation of

$e^x$

We steal the exp(x) implementation from https://github.com/recmo/experiment-solexp/blob/main/src/test/FixedPointMathLib.t.sol. This implementation has a limitation: the range is input parameter x is [-42.139678854, + 135.305999369] with 18 decimals/precision. In our case, we need to map gas excess to the range of [0, K] where K equals 135.305999369 or 135305999368893231588 in fixed point integer form.

The

$e^x$ curve can be expressed using

$$py=e^{qx}$$, as you can see below: the two parameters

$p$ and

$q$ defines the shape/slope of the curve. We need to find the right value for them, otherwise, the basefee movement will not be as expected.

(the plot above is available at https://www.desmos.com/calculator/yncurfx3ar)

Scaling

The following is how we calculate

$p$ and

$q$. Assuming the max gas excess

$M$, a uint64. then

$q=135305999368893231588/M$ (internally we keep

$q^{\prime }=q<<64$ as it fits into a uint64).

We also assuming the initial value of gasExcess is

$M/2$; and the initial basefee (the fee for purchasing 1 gas) is

$b_0$, or

$$b_0=p{e}^{(M/2+1)}+p{e}^{M/2}$$, so

$$p=b_0/(e^{(M/2+1)}+e^{M/2})$$.

It turns out the initial value of gasExcess doesn't really matter for the above calculation due to the nature of the e-curve. But choosing

$M/2$ allows price to go up and down by the same max amount.

Adjust the slope

To adjust the slope of the curve to satisfy

$R==basefee(2T)/basefee(T)$, we simply need to choose

$M$ and

$b_0$.

$b_0$ is simply to decide – if we believe the cost of a L2 transaction is

$1/n$ of the same L1 transaction, we simply use the current L1 base fee divided by

$n$. Then we can simply tune

$M$ to make sure

$R==basefee(2T)/basefee(T)$ holds. This is very simply manually a try-and-adjust approach as shown in Lib1559Math.t.sol. The TaikoL1 contract will check if

$R==basefee(2T)/basefee(T)$ holds but will not calculate

$M$ for us.

// SPDX-License-Identifier: MIT
pragma solidity 0.8.24;

library LibFixedPointMath {
    uint128 public constant MAX_EXP_INPUT = 135_305_999_368_893_231_588;
    uint256 public constant SCALING_FACTOR = 1e18; // For fixed point representation factor

    error Overflow();

    // Computes e^x in 1e18 fixed point.
    function exp(int256 x) internal pure returns (int256 r) {
        unchecked {
            // Input x is in fixed point format, with scale factor 1/1e18.

            // When the result is < 0.5 we return zero. This happens when
            // x <= floor(log(0.5e18) * 1e18) ~ -42e18
            if (x <= -42_139_678_854_452_767_551) {
                return 0;
            }

            // When the result is > (2**255 - 1) / 1e18 we can not represent it
            // as an int256. This happens when x >= floor(log((2**255 -1) /
            // 1e18) * 1e18) ~ 135.
            if (x >= 135_305_999_368_893_231_589) revert Overflow();

            // x is now in the range (-42, 136) * 1e18. Convert to (-42, 136) *
            // 2**96
            // for more intermediate precision and a binary basis. This base
            // conversion
            // is a multiplication by 1e18 / 2**96 = 5**18 / 2**78.
            x = (x << 78) / 5 ** 18;

            // Reduce range of x to (-½ ln 2, ½ ln 2) * 2**96 by factoring out
            // powers of two
            // such that exp(x) = exp(x') * 2**k, where k is an integer.
            // Solving this gives k = round(x / log(2)) and x' = x - k * log(2).
            int256 k = ((x << 96) / 54_916_777_467_707_473_351_141_471_128 + 2 ** 95) >> 96;
            x = x - k * 54_916_777_467_707_473_351_141_471_128;
            // k is in the range [-61, 195].

            // Evaluate using a (6, 7)-term rational approximation.
            // p is made monic, we'll multiply by a scale factor later.
            int256 y = x + 1_346_386_616_545_796_478_920_950_773_328;
            y = ((y * x) >> 96) + 57_155_421_227_552_351_082_224_309_758_442;
            int256 p = y + x - 94_201_549_194_550_492_254_356_042_504_812;
            p = ((p * y) >> 96) + 28_719_021_644_029_726_153_956_944_680_412_240;
            p = p * x + (4_385_272_521_454_847_904_659_076_985_693_276 << 96);

            // We leave p in 2**192 basis so we don't need to scale it back up
            // for the division.
            int256 q = x - 2_855_989_394_907_223_263_936_484_059_900;
            q = ((q * x) >> 96) + 50_020_603_652_535_783_019_961_831_881_945;
            q = ((q * x) >> 96) - 533_845_033_583_426_703_283_633_433_725_380;
            q = ((q * x) >> 96) + 3_604_857_256_930_695_427_073_651_918_091_429;
            q = ((q * x) >> 96) - 14_423_608_567_350_463_180_887_372_962_807_573;
            q = ((q * x) >> 96) + 26_449_188_498_355_588_339_934_803_723_976_023;
            assembly {
                // Div in assembly because solidity adds a zero check despite
                // the `unchecked`.
                // The q polynomial is known not to have zeros in the domain.
                // (All roots are complex)
                // No scaling required because p is already 2**96 too large.
                r := sdiv(p, q)
            }
            // r should be in the range (0.09, 0.25) * 2**96.

            // We now need to multiply r by
            //  * the scale factor s = ~6.031367120...,
            //  * the 2**k factor from the range reduction, and
            //  * the 1e18 / 2**96 factor for base conversion.
            // We do all of this at once, with an intermediate result in 2**213
            // basis
            // so the final right shift is always by a positive amount.
            r = int256(
                (uint256(r) * 3_822_833_074_963_236_453_042_738_258_902_158_003_155_416_615_667)
                    >> uint256(195 - k)
            );
        }
    }
}

/// @title LibMath
/// @dev This library offers additional math functions for uint256.
/// @custom:security-contact [e-mail]
library LibMath {
    /// @dev Returns the smaller of the two given values.
    /// @param _a The first number to compare.
    /// @param _b The second number to compare.
    /// @return The smaller of the two numbers.
    function min(uint256 _a, uint256 _b) internal pure returns (uint256) {
        return _a > _b ? _b : _a;
    }

    /// @dev Returns the larger of the two given values.
    /// @param _a The first number to compare.
    /// @param _b The second number to compare.
    /// @return The larger of the two numbers.
    function max(uint256 _a, uint256 _b) internal pure returns (uint256) {
        return _a > _b ? _a : _b;
    }
}


/// @title Lib1559Math
/// @notice Implements e^(x) based bonding curve for EIP-1559
/// @dev See https://ethresear.ch/t/make-eip-1559-more-like-an-amm-curve/9082 but some minor
/// difference as stated in docs/eip1559_on_l2.md.

library Lib1559Math {
    using LibMath for uint256;

    error EIP1559_INVALID_PARAMS();

    function calc1559BaseFee(
        uint32 _gasTargetPerL1Block,
        uint8 _adjustmentQuotient,
        uint64 _gasExcess,
        uint64 _gasIssuance,
        uint32 _parentGasUsed
    )
        internal
        pure
        returns (uint256 basefee_, uint64 gasExcess_)
    {
        // We always add the gas used by parent block to the gas excess
        // value as this has already happened
        uint256 excess = uint256(_gasExcess) + _parentGasUsed;
        excess = excess > _gasIssuance ? excess - _gasIssuance : 1;
        gasExcess_ = uint64(excess.min(type(uint64).max));

        // The base fee per gas used by this block is the spot price at the
        // bonding curve, regardless the actual amount of gas used by this
        // block, however, this block's gas used will affect the next
        // block's base fee.
        basefee_ = basefee(gasExcess_, uint256(_adjustmentQuotient) * _gasTargetPerL1Block);

        // Always make sure basefee is nonzero, this is required by the node.
        if (basefee_ == 0) basefee_ = 1;
    }

    /// @dev eth_qty(excess_gas_issued) / (TARGET * ADJUSTMENT_QUOTIENT)
    /// @param _gasExcess The gas excess value
    /// @param _adjustmentFactor The product of gasTarget and adjustmentQuotient
    function basefee(
        uint256 _gasExcess,
        uint256 _adjustmentFactor
    )
        internal
        pure
        returns (uint256)
    {
        if (_adjustmentFactor == 0) {
            revert EIP1559_INVALID_PARAMS();
        }
        return _ethQty(_gasExcess, _adjustmentFactor) / LibFixedPointMath.SCALING_FACTOR;
    }

    /// @dev exp(gas_qty / TARGET / ADJUSTMENT_QUOTIENT)
    function _ethQty(
        uint256 _gasExcess,
        uint256 _adjustmentFactor
    )
        private
        pure
        returns (uint256)
    {
        uint256 input = _gasExcess * LibFixedPointMath.SCALING_FACTOR / _adjustmentFactor;
        if (input > LibFixedPointMath.MAX_EXP_INPUT) {
            input = LibFixedPointMath.MAX_EXP_INPUT;
        }
        return uint256(LibFixedPointMath.exp(int256(input)));
    }
}