# Fully Dynamic Convex Hull

找到了一个java实现 https://github.com/yunchi/Dynamic_Convex_Hull

一个c++实现
https://code.google.com/archive/p/convex-hull-of-dynamic-set/source/default/source

@article{overmars_maintenance_1981,
	title = {Maintenance of configurations in the plane},
	volume = {23},
	issn = {00220000},
	url = {https://linkinghub.elsevier.com/retrieve/pii/002200008190012X},
	doi = {10.1016/0022-0000(81)90012-X},
	language = {en},
	number = {2},
	urldate = {2023-05-24},
	journal = {Journal of Computer and System Sciences},
	author = {Overmars, Mark H. and Van Leeuwen, Jan},
	month = oct,
	year = {1981},
	pages = {166--204},
}

想法大概是: 一个点集的凸包可以由**左半凸包**和**右半凸包**两部分组合成,(注意这里左半凸包和右半凸包不是把点集分成左半和右半两部分再求凸包, 而是整个点集并上 $(+\infty,0 )$的凸包是左半凸包) 文章说把左右两半凸包都保存在一个平衡树里面.

有这样一个lemma

> LEMMA 3.1. Given the lc- and rc-hull of a set of n points, one can determine whether an arbitrary point p lies inside, outside or on the convex hull in only $O(\log n)$ steps.

只考虑左半凸包, 判断一个给定的点是在凸包内还是在凸包上还是凸包外. binary search 找到与过给定的点的水平直线相交的凸包上的线段. 判断点在线段的左边还是右边.

计算左半凸包的过程也可以分治. 给定一个点集 $P$, 里面的点已经根据纵坐标排序, 用一个水平直线把点集 $P$ 分成两部分, 现在我们要把两个左半凸包合起来, 算出整个点集 $P$ 的左半凸包. 图中引入的 $B$ 被叫做 bridge. 实际上就是两个不相交凸包的四个 bitangent 之一. 下面有最重要的 theorem.


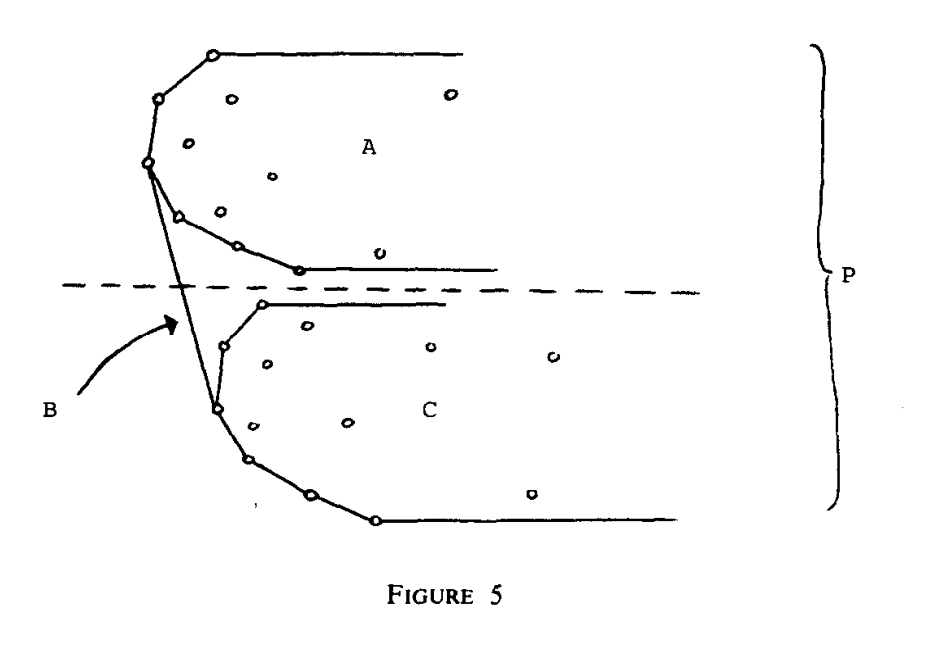
> **THEOREM 3.2. Let $p_1,p_2,...,p_n$ be $n$ arbitrary points in the plane, ordered by y-coordinate. If the representations of the lc-hull of $p_1,p_2,...,p_i$, and of $p_{i+1},...,p_n$ are known (any $1 \leq i < n$), then the lc-hull of the entire set can be built in $O(\log n)$ steps.**

实际上我们要做的就是找到 bridge. 也就是找到 bitangent. 假设途中的 A 和 C 的左半凸包都保存在平衡树里面. 都是按照 y-coordinate 排序的. 现在假设我们知道 B 是 A 中的 u 和 C 中的 d 连接起来的, 我们需要把 A 的 lc-hull(表示左半凸包) 在 u 上面的部分拿出来(包含 u), 把 C 的 lc-hull 在 d 下面的部分拿出来(包含 d), 然后把两部分合起来. 平衡树中这种操作需要 $O(\log n)$.(能concatenate和split的平衡树
https://cstheory.stackexchange.com/questions/2132/split-or-merge-binary-search-trees-in-olog-n 还有R. Sedgewick. Left-leaning red-black trees. In Dagstuhl Workshop on Data Structures, 2008. 需要看一下)

Preparata, F. P., ‘An Optimal Real-Time Algorithm for Planar Convex Hulls’, Communications of the ACM, 22.7 (1979), 402–5 <https://doi.org/10.1145/359131.359132> 文章里提到支持 binary search 就能在 $O(\log n)$ 的时间内找到某个凸包的过一个固定的点的切线. 这个文章是想搞一个在线的凸包算法, 并且每一步都只需要 $O(\log n)$. 这实际上是只有插入的动态凸包.

关于这个问题, 这本书 https://www.cs.kent.edu/~dragan/CG/CG-Book.pdf 117页 section 3.3.6 讲了 Preparata 的文章和里面提到的失败的算法. 失败的算法的想法是, 把凸包上的点按照顺时针或者逆时针的顺序保存在一个平衡树当中, 然后当要插入一个新的点 p 的时候, 首先可以用 $O(\log n)$ 的时间判断 p 是否在新的凸包上, 如果在新的凸包上就要更新凸包. 更新凸包的方法是在平衡树上找两个点 l,r, lp 和 rp 都是凸包的切线. 现在想想如何判断二分查找的指针指向的点和 p 的连线是不是当前凸包的切线. 这个判断需要花多长时间? 好像只需要两次 crossproduct 就行了. 并不需要这么复杂的过程? ... 好像这样足以告诉我们该怎么二分了.

继续 fully dynamic convex hull 当中$O(\log n)$ 找 bridge.
方法是在 A 和 C 上面同时二分查找. 每次根据 二分查找在 lc-hull A 和 lc-hull C 上选的点连线或者他们切线的交点相对于把AC分开的直线 y=m 的位置来决定哪一部分点可以被删掉. 有10种情况.


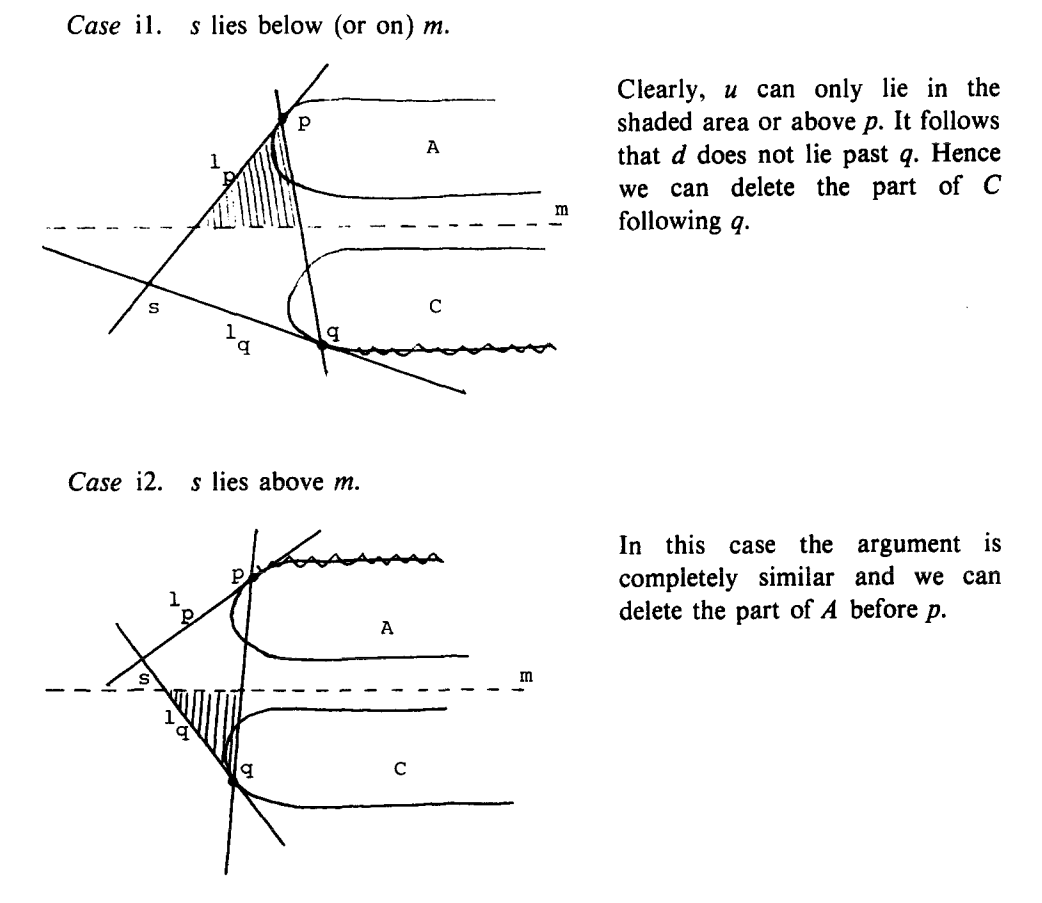
这是仅有的需要通过过 p 和 q 的切线交点和 y=m 的关系来判断的情况(关于 p 和 q 的位置, 可以像上面一样通过 pq 向量与 p 相邻的两条边的叉积来判断) 注意, 所有这些case的处理都要在 $O(1)$ 完成, 否则 binary search 就不是 $O(\log n)$!

- i1 为什么 u 一定只能在阴影区域? 因为 pq 穿过了 C 的内部, 而 p 点的切线 Lp 与 C 不一定有没有交点. 如果没有交点, 说明 C 全部位于 Lp 右侧, u 一定位于阴影区域; 如果有交点, 有可能 u 位于 p 上面, d 位于 C 的上半部分. 因此我们只能知道 d 一定不会位于 C 中 q 的后面. 我们不能去看 Lp 是否和 C 有交点, 因为这不是 $O(1)$ 的时间可以做出来的工作.
- i2 基本上一样.

依照这种方法只要两个不相交的 convex polygons 点是有序的并且支持二分查找, 我们都能用类似的方法把四个 bitangent 都找出来.

下面是插入和删除的方法.

数据是这样存的: 所有的点都按照纵坐标排序, 放在一个 binary search tree 里面. 树上的每个节点都保存一个平衡树(或者叫作 concatenable queue). 我们构建这个树的时候每个节点用 $O(\log |\# points|)$ 的时间($|\# points|$表示binary search tree节点所代表的二维点的集合大小)运行上面说的有10种情况的 binary search. 但是这里有一个问题, binary search 需要保证我们能在 $O(1)$ 的时间找到 lc-hull 中间的点, lc-hull 是用 concatenable queue 保存的(也就是平衡树), 上面10种情况的 binary search 要做到 $O(\log n)$, 合并两个 lc-hull 的时候会把子节点的 concatenable queue 破坏掉. 如果我们想恢复出两个子节点的 lc-hull, 我们需要在合并的时候保存 bridge 是加在哪个地方的, 这样向下遍历binary search tree的时候就可以把对应的部分给子节点的lc-hull接回去, 这也是一次concatenate. 一般来说需要每个 binary search tree 节点需要 $O(\log |\# points|)$.

数据结构初始化好之后就是一个二分查找树套平衡树, 二分查找树的每个点都有一个平衡树, 保存的是他的父节点没有用来构建 lc-hull 的点中属于这个儿子那一部分的点的 lc-hull.(为什么保存的是父节点没有用来构建 lc-hull ...? 和上一段合并 lc-hull 的时候把子节点的concatenable queue破坏掉的原因一样, 实际上是因为concatenable queue是平衡树, 合并的时候是把原来的两个平衡树破坏了.)(这里外层的二分查找树会把所有数据都保存在叶子节点, 中间的节点不保存实际的数据.)

在这个数据结构中, 我们想知道任何一个 binary search tree 节点的完整的 lc-hull 都只需要 $O(\log^2 n)$. 维护外层的二分查找树(平衡树)的时候, 普通的平衡树所有操作在每个节点只需要 $O(1)$ 的时间, 现在需要 $O(\log n)$, 因为要多维护 concatenable queue. 但是基本的插入/删除/rebalance操作都和普通的平衡树完全一样.