# Introduction

The goal of this zkML project is to extend the zkLLVM project
(https://github.com/NilFoundation/zkllvm) with capabilities to prove machine learning inference.

# Milestones (from Telegram)

1. Detailed spec of
1.1 ONNX standard-compliant circuits (as listed in here https://github.com/onnx/onnx-mlir/blob/main/docs/SupportedONNXOps-cpu.md) formal description. Just like we did once in here: https://github.com/NilFoundation/solana-state-proof/blob/master/docs/design/main.pdf. Some of those from ONNX standard are already present on our side - let's coordinate about this.
1.2 Analysis about if there is sense to reduce from MLIR to LLVM IR.
1.3 If it makes sense, then how to lower MLIR to LLVM IR efficiently enough and which extensions LLVM IR has to have.
1.4 More efficient circuits definition done for a particular example use case. (Example should be big and ambitious one for this to worth it to you guys, so let's make it some trivial LLM-alike one? We have some circuit estimations about such one)
1.5 Analysis about necessary proof system efficiency improvements.

2. ONNX-frontend implementation.

3. Example use case implementation.

# Some Questions

1) Regarding the ONNX standard-compliant circuits, we think, at least for the initial report, it makes sense to limit the ops for circuit definitions to the most important/common ones used (to not bust scope). ReLU, Average/MaxPool, Convolution, SoftMax and Fully Connected Layers. Would you agree on the list or add/change some? Of course, others can be added in future milestones.
2) You said you already started on those circuits, would it be possible to give us insight in this work? Especially, what circuits do you already have and are these manually built from the ONNX blocks or created from MLIR or LLVM IR?
3) Also, are these circuit representations even that relevant if we lower from ONNX->MLIR->LLVM IR? At least in our understanding of the toolchain, if we built it like this we either need pattern recognition to reconstruct the ONNX blocks/ops or the LLVM compiler takes automatically care of arithmetization without the circuit building blocks, where the efficiency is questionable (re 1.3 above).

*The critical question is whether to target components at the ONNX layer or the MLIR layer (even before going down to LLVMIR), since the scope and usefulness of the above mentioned components depends heavily on this decision.*

Just to be sure we are on the same page, for us‚ this is an example of a MaxPool layer in MLIR.

 affine.for %arg1 = 0 to 1 {
      affine.for %arg2 = 0 to 1 {
        affine.for %arg3 = 0 to 14 {
          affine.for %arg4 = 0 to 14 {
            affine.store %cst_0, %alloca[] : memref<f32>
            %4 = affine.max #map(%arg3)
            %5 = affine.max #map(%arg4)
            affine.for %arg5 = 0 to min #map1(%arg3)[%c28, %c2, %c0, %c2, %c1] {
              affine.for %arg6 = 0 to min #map1(%arg4)[%c28, %c2, %c0, %c2, %c1] {
                %7 = arith.addi %arg5, %4 : index
                %8 = arith.addi %arg6, %5 : index
                %9 = memref.load %arg0[%arg1, %arg2, %7, %8] : memref<1x1x28x28xf32>
                %10 = affine.load %alloca[] : memref<f32>
                %11 = arith.cmpf ogt, %10, %9 : f32
                %12 = arith.select %11, %10, %9 : f32
                affine.store %12, %alloca[] : memref<f32>
              }
            }
            %6 = affine.load %alloca[] : memref<f32>
            affine.store %6, %alloc[%arg1, %arg2, %arg3, %arg4] : memref<1x1x14x14xf32>
          }
        }
      }
    }

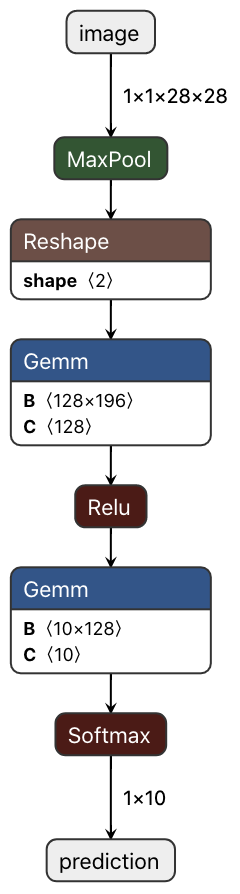
And this is the ONNX layer, i.e., the graph of ONNX blocks/ops: