# 2020q3 Homework4 (quiz4)
contributed by < `ptzling310` >
> [2020q3 第 4 週測驗題](https://hackmd.io/@sysprog/2020-quiz4)
## 測驗 `1`: LeetCode [461. Hamming Distance](https://leetcode.com/problems/hamming-distance/)
```c
int hammingDistance(int x, int y) {
return __builtin_popcount(x OP y);
}
```
- [x] OP = `^`
## 理解

觀察:
Distance( (0100)~2~ , (1001)~2~ ) = 3
Distance( (0110)~2~ , (1110)~2~ ) = 1
恰為兩數取 `XOR` 後, bit 1 的個數。 故 OP 為 `^`。
### 不使用 gcc extension 的 C99 實作程式碼
:::spoiler [詳解二進位數中 1 的個數](http://github.tiankonguse.com/blog/2014/11/16/bit-count-more.html)
```
101100 (44)
101011 (44-1)
------------------
44 與 43 的後 3 位相反
101100 (44)
& 101011 (43)
-------------------
101000 (40)
比原本的 44 相比,少了最右邊的 bit 1
101000 (40)
100111 (40-1)
-------------------
40 與 39 的後 4 位相反
101000 (40)
& 100111 (40-1)
-------------------
100000 (32)
比原本的 40 相比,少了最右邊的 bit 1
100000 (32)
011111 (31)
------------------
32 與 31 的後 6 位相反
100000 (32)
& 011111 (31)
------------------
000000 (0)
∴ bit 1 的個數與上述運算直至 0 的次數相等,可利用此技巧來計算二進制中 bit 1 的個數。
```
:::
```c
int hammingDistance(int x, int y){
int dist = x ^ y;
int n = 0 ;
while(dist && (++n , dist&=dist-1));
return n;
}
```
參考[詳解二進位數中 1 的個數](http://github.tiankonguse.com/blog/2014/11/16/bit-count-more.html)的方式,將 `x^y` 不斷的做 `-1` 再取 `&` 直到求出結果為 `0`,最終將計算次數記錄到變數 `n` 當中,則 `n` 就是 `x^y` 的 bit 1 個數了。

### [477. Total Hamming Distance](https://leetcode.com/problems/total-hamming-distance/)
:::spoiler Runtime: Time Limit Exceeded
```c
int hammingDistance(int x, int y) {
return __builtin_popcount(x ^ y);
}
int totalHammingDistance(int* nums, int numsSize){
if(nums == NULL || numsSize == 0) return 0;
int result=0;
for (int i=0; i < numsSize ; i++){
for (int j= i+1 ; j < numsSize ; j++){
result += hammingDistance(nums[i],nums[j]);
}
}
return result;
}
```

根據網頁上的 explain ,一次取兩個數去做 `hammingDistance`,但這樣會超時。
:::
```
Input: 4, 14, 2
Output: 6
c1 c2 c3 c4
4 = ( 0 1 0 0 )
14= ( 1 1 1 0 )
2 = ( 0 0 1 0 )
```
觀察每一個 column:
```
c4: 皆為 0 ,因為概念還是要用 `XOR` , 所以若沒有相異的 bit ,並不會增加 total distance。
c3:針對有 bit 1 出現的 14 以及 2。會個別與 4 的 bit 0 做 `XOR` 會增加 total distance。故 c3 應該會產生 2 的距離。
c2:同 c3 的情況,產生 2 的距離。
c1:只有 14 有 bit 1,分別與 4 以及 2 的 bit 0 做 `XOR` 可增加 total distance 2。
```
綜合上述, total distance 應為 `2 + 2 + 2` = 6。
再來,探討如何達到上述討論的運算,如果我們藉由一次看一個去,去和其他數比較,那麼也會有超時的問題。所以在本題的 dicussion 中,討論出如何達到計算出每個 column 貢獻的距離。
藉由計算==每個 column 的 bit 0 以及 bit 1 的個數,再將兩數相乘==即得每個 column 所貢獻的距離,再加總即得 total hamming distance。
```c
int totalHammingDistance(int* nums, int numsSize)
{
if(nums == NULL || numsSize == 0) return 0;
int result = 0; //紀錄最後的distance
for(int i = 0 ; i <31 ; i++){
int count_one = 0;
for(int j = 0 ; j < numsSize ; j++){
if(nums[j] & (1<<i))
count_one++;//計算bit 1
}
result += count_one * (numsSize-count_one);
}
return result;
}
```

:::warning
TODO:時間還可以再改進。
因為這個版本仍是一個 bit 一個 bit 的檢查,
不過目標是再看 bit 1 ,那就聯想到 gcc extension!
:::
------------------------------------
## 測驗 `2`: LeetCode [1483. Kth Ancestor of a Tree Node](https://leetcode.com/problems/kth-ancestor-of-a-tree-node/)
>給你一棵樹,樹上有 n 個節點,編號自 0 到 n−1。樹以父節點陣列的形式提供,其中 parent[i] 是節點 i 的父節點。樹的根節點是編號為 0 的節點。請設計 treeAncestorGetKthAncestor(TreeAncestor *obj, int node, int k) 函式,回傳節點 node 的第 k 個祖先節點。若不存在這樣的祖先節點,回傳 -1。樹節點的第 k 個祖先節點是從該節點到根節點路徑上的第 k 個節點。
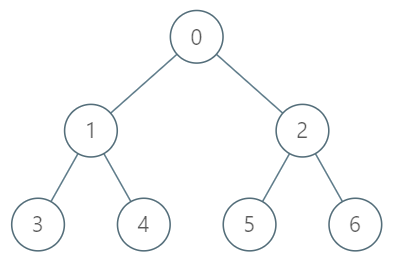
```
Input:
["TreeAncestor","getKthAncestor","getKthAncestor","getKthAncestor"]
[[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]]
Output:
[null,1,0,-1]
```
:::spoiler 完整程式
```c=
#include <stdlib.h>
typedef struct {
int **parent;
int max_level;
} TreeAncestor;
TreeAncestor *treeAncestorCreate(int n, int *parent, int parentSize)
{
TreeAncestor *obj = malloc(sizeof(TreeAncestor));
obj->parent = malloc(n * sizeof(int *));
int max_level = 32 - __builtin_clz(n) + 1;
for (int i = 0; i < n; i++) {
obj->parent[i] = malloc(max_level * sizeof(int));
for (int j = 0; j < max_level; j++)
obj->parent[i][j] = -1;
}
for (int i = 0; i < parentSize; i++)
obj->parent[i][0] = parent[i];
for (int j = 1;; j++) {
int quit = 1;
for (int i = 0; i < parentSize; i++) {
obj->parent[i][j] = obj->parent[i][j -1] == -1
? -1
: obj->parent[obj->parent[i][j - 1]][j - 1];
if (obj->parent[i][j] != -1) quit = 0;
}
if (quit) break;
}
obj->max_level = max_level - 1;
return obj;
}
int treeAncestorGetKthAncestor(TreeAncestor *obj, int node, int k)
{
int max_level = obj->max_level;
for (int i = 0; i < max_level && node != -1; ++i)
if (k & (1<<i))
node = obj->parent[node][i];
return node;
}
void treeAncestorFree(TreeAncestor *obj)
{
for (int i = 0; i < obj->n; i++)
free(obj->parent[i]);
free(obj->parent);
free(obj);
}
```
:::
### 理解
#### Struct
```c
typedef struct {
int **parent;
int max_level;
} TreeAncestor;
```
在 `*treeAncestorCreate` 中:
```c
TreeAncestor *obj = malloc(sizeof(TreeAncestor));
obj->parent = malloc(n * sizeof(int *));
```
觀察 `obj->parent` ,這是分配 n 個 指標空間,所以 `parent` 指向的是指標。
所以 AAA = `int **parent`。
#### treeAncestorCreate
```c=13
int max_level = 32 - __builtin_clz(n) + 1;
```
可以計算出 n 個 node 下, 一個 Binary Tree 有幾 level。若 n = 7 =(0...0111)~2~ ,則 max_level = 32 - 29 + 1 = 4。 n = 13 = (0..1101)~2~,則 max_level = 32 - 28 + 1 = 5。
:::spoiler ~~節點數(n) 與 level 的關係~~
觀察 binary tree 的 結構。
| Level | 最大 Node 數 (n) | |
| -------- | -------- | -------- |
| 1 | 1 | $2^1-1$ |
| 2 | 3 | $2^2-1$ |
| ...|...|...
| l | | $2^l-1$|
所以 level 為 l 之 binary tree 最多會有 $2^n-1$ 個 nodes。當我們知道 n 個點時,就可以反推 level !
$2^l-1=n$
$2^l=n+1$
$l= \lceil log_2(n+1)\rceil= log_2(n)+1$
但為何$log_2(n)+1$ = 32 - __builtin_clz(n)?
計算 $log_2(n)$ 也可以利用位移操作,
```
Log2(x) = result;
while (x >>= 1) result++;
```
`*` level 從 `1` 開始計算。
所以本程式就是這兩行程式的改寫。
為何刪除?
原本認為 `parent[i][j]` 的 j 應為階層數,
也就是 `parent[i][j]` 即是 node i 的第 j 代祖先。
但在後續解釋不通。故刪除此推測。
:::
```c=14
for (int i = 0; i < n; i++) {
obj->parent[i] = malloc(max_level * sizeof(int));
for (int j = 0; j < max_level; j++)
obj->parent[i][j] = -1;
}
```
產生二維陣列 `parent[n][max-level]`。
將陣列的內容都預設為 `-1`。
| [i] \ [j] | 0 | 1 | 2 | 3 |
| -------- | -------- | -------- |-------- |-------- |
| 0 | -1 | -1 | -1 | -1 |
| 1 | -1 | -1 | -1 | -1 |
| 2 | -1 | -1 | -1 | -1 |
| 3 | -1 | -1 | -1 | -1 |
| 4 | -1 | -1 | -1 | -1 |
| 5 | -1 | -1 | -1 | -1 |
| 6 | -1 | -1 | -1 | -1 |
```c=19
for (int i = 0; i < parentSize; i++)
obj->parent[i][0] = parent[i];
```
將 input 的 [-1,0,0,1,1,2,2] 填入,
所以 `parent[i][0]` 會記錄節點 i 的父點(前一代)
| [i] \ [j] | 0 | 1 | 2 | 3 |
| -------- | -------- | -------- |-------- |-------- |
| 0 | -1 | -1 | -1 | -1 |
| 1 | 0 | -1 | -1 | -1 |
| 2 | 0 | -1 | -1 | -1 |
| 3 | 1 | -1 | -1 | -1 |
| 4 | 1 | -1 | -1 | -1 |
| 5 | 2 | -1 | -1 | -1 |
| 6 | 2 | -1 | -1 | -1 |
```c=22
for (int j = 1;; j++) {
int quit = 1;
for (int i = 0; i < parentSize; i++) {
obj->parent[i][j] = obj->parent[i][j + BBB] == -1
? -1
: obj->parent[obj->parent[i][j - 1]][j - 1];
if (obj->parent[i][j] != -1) quit = 0;
}
if (quit) break;
}
```
`parent[i][j]` 是紀錄 node i 的第前 $2^{j}$ 代祖先。
`j` 從 1 開始,所以第一次迴圈會到 `parent[0][1]` 。
`obj->parent[i][j + BBB] == -1`
要討論 i 的第前 $2^j$ 代時,先檢查 i 的第前 $2^{j-1}$ 代是否存在。
```
假設目前 i = 0, j = 2,想知道 node 0 的第前 2 代,
先檢查 node 0 的第前 1 代是否存在 (查表可知 parent[0][1] = -1 所以不存在),
這樣也沒必要重新設定 node 0 的第前 2 代了,維持原來的值 -1 即可。
```
故 BBB = `-1`。
:::spoiler Trace
- 在 `parent[0][1]` ,由於`obj->parent[0][0] = -1` ,故不修改 `parent[0][1]` 之值(維持 -1)。接著 quit 不符合 `if` 要求,故值維持 1 ,執行 `break`。結束 node 0 的設定。
- 在 `parent[1][1]` ,由於`obj->parent[1][0]` = 0 ≠ -1 ,所以要修改 `parent[1][1]` 的值。
`obj->parent[ obj->parent[1][0] ][0]` = `obj->parent[0][0]` = -1 。在進入 `parent[1][2]` 時,會因為`obj->parent[1][1]` = -1,而停止對 node 1 的設定。
- `parent[3][1]` 要修改值為:
`obj->parent[obj->parent[3][0]][0]` = `obj->parent[1][0]` = 0
- `parent[3][2]` 要修改值為:
`obj->parent[obj->parent[3][1]][1]` = `obj->parent[0][0]` = -1
- `parent[5][1]` 要修改值為:
`obj->parent[obj->parent[5][0]][0]` = `obj->parent[2][0]` = 0
- `parent[5][2]` 要修改值為:
`obj->parent[obj->parent[5][1]][1]` = `obj->parent[0][0]` = -1
:::
| [i] \ [j] | 0 | 1 | 2 | 3 |
| -------- | -------- | -------- |-------- |-------- |
| 0 | -1 | -1 | -1 | -1 |
| 1 | 0 | -1 | -1 | -1 |
| 2 | 0 | -1 | -1 | -1 |
| 3 | 1 | 0 | -1 | -1 |
| 4 | 1 | 0 | -1 | -1 |
| 5 | 2 | 0 | -1 | -1 |
| 6 | 2 | 0 | -1 | -1 |
先前推測 `parent[i][j]` 是紀錄 node i 的第前 j 代祖先,
觀察此表,應為:`parent[i][j]` 是紀錄 node i 的第前 $2^{j}$ 代祖先
所以 `parent[1][2]` 是 node 1 的 第前 $2^2=4$ 代祖先, 不存在,故為 -1 。
```c=32
obj->max_level = max_level - 1;
```
如果不進行加一的話呢?則在某些狀況下會無法在 table 中產生全為 `-1` 的 colume。
(參考 [`Rsysz`的共筆](https://hackmd.io/@Rsysz/quiz4#%E5%BB%B6%E4%BC%B8%E5%95%8F%E9%A1%8C1),有舉出會產生錯誤的例子! )
#### treeAncestorGetKthAncestor
```c=40
if (k & ( 1 << i ))
node = obj->parent[node][i];
```
由於是 `return node`, 故這裡的 `node` 就是我們所要回傳的祖先的編號。
代表應該是藉由此段程式碼移動所要回傳的 node 為止。
```
這裡利用 n = 14 的 full binary tree 來舉例討論。
0
/ \
1 2
/ \ / \
3 4 5 6
/ \ / \ / \ / \
7 8 9 10 11 12 13 14
```
當想要知道 node 7 的第 2 代祖先 (應為 1)
| k | i | 1<<i | k&(1<<i) | node = parent[node][i] |
| -------- | -------- | -------- |-------- |-------- |
| 2 = (0010)~2~ | 0 | (0001)~2~ | (0000)~2~ |不進入 if |
| | 1 | (0010)~2~ | (0010)~2~ |node = parent[7][1]=1 |
現在想要知道 node 7 的第 3 代祖先 (應為 0)
| k | i | 1<<i | k&(1<<i) | node = parent[node][i] |
| -------- | -------- | -------- |-------- |-------- |
| 3 = (0011)~2~ | 0 | (0001)~2~ | (0001)~2~ | node = parent[7][0]=3|
| | 1 | (0010)~2~ | (0010)~2~ | node = parent[3][1]=0|
由於在 table 中是紀錄 i 的第 $2^j$,若所欲存取的第 k 代祖先為二的冪,則 k 的二進制中必定只有一個 bit 1 出現,則我們的 node 只會移動一次。
若 k 不為二的冪,則依照 bit 1 的數量移動,如上例 k = 3 = (0011)~2~,我們就需要先讀走到 node 3,變成讀取 node 3 的第 $2^1 = 2$ 代祖先。
#### treeAncestorFree
```c=47
for (int i = 0; i < obj->n; i++)
free(obj->parent[i]);
free(obj->parent);
free(obj);
```
在 `treeAncestorFree` 中沒有定義到 `n` 為何。可以看的出來 n 就是紀錄節點數,由於這裡是使用 `obj->n` 來做判斷,故在 struct 中,必須加上 `n`。 這樣程式才能夠執行。
- `struct` 的修正
```diff
typedef struct {
int **parent;
int max_level;
+ int n;
} TreeAncestor;
```
- `treeAncestorCreate` 的修正
```diff
TreeAncestor* treeAncestorCreate(int n, int* parent, int parentSize) {
TreeAncestor *obj = malloc(sizeof(TreeAncestor));
+ obj-> n = n;
obj->parent = malloc(n * sizeof(int *));
...
}
```
-------------
## 測驗 `3`:[FizzBuzz](https://en.wikipedia.org/wiki/Fizz_buzz)
>從 1 數到 n,如果是 3的倍數,印出 “Fizz”
如果是 5 的倍數,印出 “Buzz”
如果是 15 的倍數,印出 “FizzBuzz”
如果都不是,就印出數字本身
```
n :1 2 3 4 5 6 7 ... 14 15
1 2 Fizz 4 Buzz Fizz 7 ... 14 FizzBuzz ....
```
```c=
#define MSG_LEN 8
static inline bool is_divisible(uint32_t n, uint64_t M) {
return n * M <= M - 1;
}
static uint64_t M3 = UINT64_C(0xFFFFFFFFFFFFFFFF) / 3 + 1;
static uint64_t M5 = UINT64_C(0xFFFFFFFFFFFFFFFF) / 5 + 1;
int main(int argc, char *argv[]) {
for (size_t i = 1; i <= 100; i++) {
uint8_t div3 = is_divisible(i, M3);
uint8_t div5 = is_divisible(i, M5);
unsigned int length = (2 << div3) << div5;
char fmt[MSG_LEN + 1];
strncpy(fmt, &"FizzBuzz%u"[(MSG_LEN >> KK1) >> (KK2 << KK3)], length);
fmt[length] = '\0';
printf(fmt, i);
printf("\n");
}
return 0;
}
```
- [x] KK1 = `div5`
- [x] KK2 = `div3`
- [x] KK3 = `2`
#### 觀念
```
string literal: "fizzbuzz%u"
offset: 0 4 8
當為 3 的倍數:印 [0~3]
當為 5 的被數:印 [4~7]
當為 15 的倍數:印 [0~7]
其他:印 [8]
```
### 理解
```c=3
static inline bool is_divisible(uint32_t n, uint64_t M) {
return n * M <= M - 1;
}
static uint64_t M3 = UINT64_C(0xFFFFFFFFFFFFFFFF) / 3 + 1;
static uint64_t M5 = UINT64_C(0xFFFFFFFFFFFFFFFF) / 5 + 1;
```
參照[判斷某個數值能否被指定的除數所整除](https://hackmd.io/159Bz7qOSPaPUOSPg3ie0A#%E6%B8%AC%E9%A9%97-4%EF%BC%9A-%E5%88%A4%E6%96%B7%E6%9F%90%E5%80%8B%E6%95%B8%E5%80%BC%E8%83%BD%E5%90%A6%E8%A2%AB%E6%8C%87%E5%AE%9A%E7%9A%84%E9%99%A4%E6%95%B8%E6%89%80%E6%95%B4%E9%99%A4)。
```c=12
uint8_t div3 = is_divisible(i, M3);
uint8_t div5 = is_divisible(i, M5);
unsigned int length = (2 << div3) << div5;
```
觀察:
| i | div3 | div5 | print|start|length|
| -------- | -------- | -------- | -------- | -------- |-------- |
| i % 3 == 0 | 1 | 0 | Fizz|0|4|
| i % 5 == 0 | 0 | 1 | Buzz|4|4|
| i % 15 == 0 | 1 | 1 |FizzBuzz|0|8|
| 其他 | 0 | 0 |i|8|2|
`length` 在 `div3 = 0` 即 `div5 = 0` 的情況下,會為 2 = (0..010)~2~;
若 `div3 = 1` 或 `div5 = 1 ` 的情況下,會為 `2 << 1` = (0...0100)~2~ = 4;
在 `div3 = 1` 且 `div5 = 1 ` 的情況下,會為 `(2 << 1) << 1` = (0..01000)~2~ = 8。
故藉此法,可控制 `length` 為何。
```c=16
char fmt[MSG_LEN + 1]; //char fmt[9];
strncpy(fmt, &"FizzBuzz%u"[(MSG_LEN >> div3) >> (div5 << 2)], length);
```
建立一個陣列: `fmt`,可存9個 char。
`struncpy(目的,來源,長度)`,由於 `"FizzBuzz%u"` 並不是要從頭複製,所以後面要再去設定起始位置。`[(MSG_LEN >> KK1) >> (KK2 << KK3)]` 即是上表的 `start`,KK1、KK2應該與`div3`、`div5` 有關。
- 採 KK1 = `div3` , KK2 = `div5`。`MSG_LEN` = 8 = (1000)~2~
- 若 KK1 = `div3` = 1;KK2 = `div5` = 0
```
(MSG_LEN >> KK1) : (1000) >> 1 = (0100)
(KK2 << KK3) : (0000) << KK3 = (0000)
(MSG_LEN >> KK1) >> (KK2 << KK3) : (0100) >> (0000) = (0100) = 4
```
但目標 `start` 應該為 `0`,故此假設是錯的。
- 採 KK1 = `div5` , KK2 = `div3`。`MSG_LEN` = 8 = (1000)~2~
- 若 KK1 = `div5` = 0;KK2 = `div3` = 1
```
(MSG_LEN >> KK1) : (1000) >> 0 = (1000)
(KK2 << KK3) : (0001) << KK3
(MSG_LEN >> KK1) >> (KK2 << KK3) : (1000) >> ( (0001) << KK3 ) = 0
```
為了達到 `start` = 0,利用 KK3 來進行修正,(1000)~2~ 還需右移 4 才會變 0,
所以 `( (0001) << KK3 )` = 4 , KK3 = `2`。
- 若 KK1 = `div5` = 1;KK2 = `div3` = 0
```
(MSG_LEN >> KK1) : (1000) >> 1 = (0100)
(KK2 << KK3) : (0000) << KK3 = (0000)
(MSG_LEN >> KK1) >> (KK2 << KK3) : (0100) << 0 = 4
```
這裡 KK3 不論是多少都不會有作用,不過結果是對的。
- 若 KK1 = `div5` = 1;KK2 = `div3` = 1
```
(MSG_LEN >> KK1) : (1000) >> 1 = (0100)
(KK2 << KK3) : (0001) << 2 = (0100)
(MSG_LEN >> KK1) >> (KK2 << KK3) : (0100) >> (0100) = 0
```
- 若 KK1 = `div5` = 0;KK2 = `div3` = 0
```
(MSG_LEN >> KK1) : (1000) >> (0000) = (1000)
(KK2 << KK3) : (0000) >> 2 = (0000)
(MSG_LEN >> KK1) >> (KK2 << KK3) : (1000) >> (0000) = (1000)
```
結果正確,所以KK1 = `div5` , KK2 = `div3` , KK3 = `2`。
```c=18
fmt[length] = '\0';
```
補上結尾符號。
### 評估 naive.c 和 bitwise.c 效能落差
這裡設定 n = 100,000。
#### naive.c
`$ sudo perf stat ./naive`
```
Performance counter stats for './naive':
229.68 msec task-clock # 0.110 CPUs utilized
10 context-switches # 0.044 K/sec
0 cpu-migrations # 0.000 K/sec
53 page-faults # 0.231 K/sec
6,2726,9708 cycles # 2.731 GHz
4,6991,1124 instructions # 0.75 insn per cycle
9389,8810 branches # 408.828 M/sec
126,5634 branch-misses # 1.35% of all branches
2.081604900 seconds time elapsed
0.044511000 seconds user
0.186140000 seconds sys
```
#### bitwise.c
`$ sudo perf stat ./bitwise`
```
Performance counter stats for './bitwise':
342.36 msec task-clock # 0.088 CPUs utilized
7 context-switches # 0.020 K/sec
0 cpu-migrations # 0.000 K/sec
52 page-faults # 0.152 K/sec
12,1452,9781 cycles # 3.548 GHz
8,7415,3716 instructions # 0.72 insn per cycle
1,7315,6927 branches # 505.778 M/sec
257,6487 branch-misses # 1.49% of all branches
3.874382673 seconds time elapsed
0.075787000 seconds user
0.267251000 seconds sys
```
藉由測驗所提供的程式,在 n = 100,000 的情況下,`navie.c` 的執行時間較短。
-------------------------------------------
## 測驗 `4`:PAGE_QUEUES
用最少的 case-break 敘述做出同等 `size_t blockidx = offset / PAGE_QUEUES;` 效果的程式碼。
```c=
#include <stdint.h>
#define ffs32(x) ((__builtin_ffs(x)) - 1)
size_t blockidx;
size_t divident = PAGE_QUEUES;
blockidx = offset >> ffs32(divident);
divident >>= ffs32(divident);
switch (divident) {
CASES
}
```
其中 CASES 可能形如:
```c
case 2: blockidx /= 2;
break;
```
CASES:`3`、`5`、`7`
### 理解
```c=2
#define ffs32(x) ((__builtin_ffs(x)) - 1)
```
`__builtin_ffs(x)`:Returns one plus the index of the ==least significant 1-bit== of x, or if x is zero, returns zero. 這邊再做一個 `-1`的動作,就可以得出最右的 bit 1 右邊又有幾個 bit 0。
```
12 = (1100)
__builtin_ffs(12) = 3
__builtin_ffs(12) - 1 = 2
故從右邊數會先經過 2 個 bit 0,來到第三個 bit 才會為 bit 1。
```
```c=3
blockidx = offset >> ffs32(divident);
divident >>= ffs32(divident);
```
原本 `blockidx` 的計算為 $\dfrac{offset}{PAGE-QUEUES}$,
這裡每次都是處理$2^n$,也就是 $\dfrac{\dfrac{offset}{2^n}}{\dfrac{PAGE-QUEUES}{2^n}}$ 處理。
程式中的 line 2 就是再找 $2^n$,找到我們就直接右移處理,不必使用除法。
回頭看 `PAGE_QUEUES` 的可能範圍:
- (1 or 2 or 3 or 4)
- (5 or 6 or 7 or 8) × ($2^n$), n from 1 to 14
觀察 `ffs32(divident)`:
| divident(PAGE_QUEUES) | 二進制 | ffs32(divident) | divident >>= ffs32(divident)
| -------- | -------- | -------- |-------- |
| 1 | (0001)~2~ | 0 | (0001)~2~ = 1 |
| 2 | (0010)~2~ | 1 | (0001)~2~ = 1 |
| 3 | (0011)~2~ | 0 | (0011)~2~ = 3 |
| 4 | (0100)~2~ | 2 | (0001)~2~ = 1 |
| 5 x $2^n$ | (01010...0)~2~| n | (0101)~2~ = 5 |
| 6 x $2^n$ | (01100...0)~2~| n+1 | (0011)~2~ = 3 |
| 7 x $2^n$ | (01110...0)~2~| n | (0111)~2~ = 7 |
| 8 x $2^n$ | (10000...0)~2~| n+3 | (0001)~2~ = 1 |
所以`divident >>= ffs32(divident)` 只會有`1`、`3`、`5`、`7`這三種可能。
由於已經沒辦法使用右移來代替除法運算,所以依照不同可能進行除法運算。
這裡的 `swithch` 應為:
```c
switch (divident) {
case 1: blockidx /= 1;
break;
case 3: blockidx /= 3;
break;
case 5: blockidx /= 5;
break;
case 7: blockidx /= 7;
break;
}
```
而又因為 `/1` 其實對數字本身沒有作用,所以只需處理`3`、`5`、`7`的部分即可。
--------------------------------------------
###### tags: `sysprog2020`
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet