Leetcode刷題學習筆記–Tree Traversal

Introduction

ref : Tree Traversals (Inorder, Preorder and Postorder)

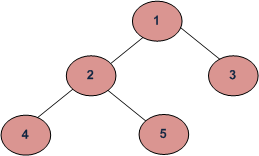
1. pre-order
   順序 : parent -> left -> right, 從top -> bottom
   適用於要先決定好parent才可以決定child。
   1->2->4->5->3
   

2. in-order
   順序 : left child -> parent -> right child, 從bottom ->top
   4->2->5->1->3
   

   
   在binary search tree(BST)中，使用inorder可以得到由小到大的排序。

3. post-order
   順序 : left child -> right child -> parent, 從bottom -> top
   適用於要先決定好child才可以決定parent
   4->5->2->3->1
   

4. level-order(BFS)
   

Problems

653. Two Sum IV - Input is a BST

給定一個target，找出在BST中是否有兩個node加起來為target。
想法:

1. 把node全部讀出來放入unordered_set
2. 如果不用額外的空間，只在tree中尋找。(下面code的解法)，這個也算是DFS的pre-order尋訪。如果是balanced binary tree則效率為O(logN)

TreeNode* findNode(TreeNode *root, int val) {
    if(!root) return nullptr;
    if(root->val == val) return root;
    if(val > root->val) return findNode(root->right, val);
    else return findNode(root->left, val);
}
    
bool helper(TreeNode* root, TreeNode* curr, int k) {
    TreeNode* target;
    if(!curr) return false;
    target = findNode(root, k - curr->val);
    if(target && target != curr)
        return true;
    else 
        return helper(root, curr->left, k) || helper(root, curr->right, k);  
}
    
bool findTarget(TreeNode* root, int k) {
    if(!root) return false;
    return helper(root, root, k);
}

199. Binary Tree Right Side View

給一個binary tree只輸出最右邊的value。典型的level-order traversal。

void helper(vector<TreeNode *>& q, vector<int>& rtn) {
    if(q.size() == 0) return;
    vector<TreeNode *> newq;
        
    for(TreeNode *node : q) {
        if(node->left)
            newq.push_back(node->left);
        if(node->right)
            newq.push_back(node->right);
    }
    rtn.push_back(q.back()->val);
    helper(newq, rtn);
}
    
vector<int> rightSideView(TreeNode* root) {
    if(!root) return {};
        
    vector<int> rtn;
    vector<TreeNode *> q;
        
    if(root->left)
        q.push_back(root->left);
    if(root->right)
        q.push_back(root->right);
    rtn.push_back(root->val);
    helper(q, rtn);
        
    return rtn;
}

1008. Construct Binary Search Tree from Preorder Traversal(Medium)

給你一個用preorder排序過的vector，根據這個vector重建binary tree。

1. 第一個數值一定是root
2. 因為binary tree的特性是右邊的數值一定大於root，所以找出比第一個數值大的分界點。
3. 利用recursive來產生左右邊的sub-tree。
   ps: 可以用使只傳遞上下邊界來改善效能。

TreeNode* bstFromPreorder(vector<int>& preorder) {
    auto n = preorder.size();
    if(n == 0) return nullptr;
    else if(n == 1) return new TreeNode(preorder[0]);
    else {
        auto pos = upper_bound(preorder.begin() + 1, preorder.end(), preorder[0]);
        vector<int> left(preorder.begin() + 1, pos);
        vector<int> right(pos, preorder.end());
        return new TreeNode(preorder[0], 
                                bstFromPreorder(left),
                                bstFromPreorder(right));
    }
}

617. Merge Two Binary Trees(Easy)

給你兩個binary tree, 如果位置一樣的node兩個tree都有，就把node的數值相加，不然就是取有的那個node。

1. 重複使用node，避免新增node。
2. 把數值都往root1加。
3. 取root->left或root->right的時候，要先判斷root是否為null。

TreeNode* helper(TreeNode *root1, TreeNode *root2) {
    if(!root1 && !root2) return nullptr;
    else if(!root1) return root2;
    else if(!root2) return root1;
    else {
        root1->val += root2->val;
        return root1;
    }
}    
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
    TreeNode *newroot = helper(root1, root2);
    if(newroot) {
        newroot->left = mergeTrees(
            root1 ? root1->left : nullptr,
            root2 ? root2->left : nullptr);
        newroot->right = mergeTrees(
            root1 ? root1->right : nullptr,
            root2 ? root2->right : nullptr);
    }        
    return newroot;
}

1026. Maximum Difference Between Node and Ancestor(Medium)

給你一個binary tree,找出任一node和parent最大的差值。

1. 不是一個BST，所以最大最小值不是最頂點的node。
2. 因為差值是取abs，所以必須紀錄最大最小值。

int helper(TreeNode *node, int maxv, int minv) {
    if(!node) return -1;
    int rtn = max(abs(maxv - node->val), abs(minv - node->val));
    // 紀錄一路過來的最大最小值。因為差值是取abs
    maxv = max(maxv, node->val);
    minv = min(minv, node->val);
    return max(rtn, 
        max(helper(node->left, maxv, minv), 
            helper(node->right, maxv, minv)));
    }
    int maxAncestorDiff(TreeNode* root) {
        return max(helper(root->left, root->val, root->val),
                   helper(root->right, root->val, root->val));
}

572. Subtree of Another Tree(Easy)

給你兩個binary tree(root, subRoot)，判斷root中是否有subtree和subRoot一樣。

1. 問題如果是問兩顆tree一不一樣，問題就簡單多了，只要用下面的isSameTree()來判斷。
2. 但是問題是問在root中的subtree，所以尋訪整個tree，如果第一的node數值一樣，就使用isSameTree()來判斷是不是一樣。

bool isSameTree(TreeNode *root, TreeNode *subRoot) {
    if(!root && !subRoot) return true;
    else if(!root || !subRoot) return false;
    else {
        if(root->val == subRoot->val)
            return isSameTree(root->left, subRoot->left) && 
                   isSameTree(root->right, subRoot->right);
        else
            return false;
    }
}

bool isSubtree(TreeNode* root, TreeNode* subRoot) {
    if(!root) return false;
    else if(isSameTree(root, subRoot))
        return true;
    else
        return isSubtree(root->left, subRoot) || 
               isSubtree(root->right, subRoot);
}

1022. Sum of Root To Leaf Binary Numbers(Easy)

給你一個binary，從root到leaf可以表示成一個binary數值，求出所有binary數值的和。

1. 所有進入helper()退出來的時候必須把原本加進去的數值退掉。

void helper(TreeNode *root, int& sum, int& cur) {
    cur = (cur << 1) + root->val;
    if(!root->left && !root->right) { 
        sum += cur;
        return;
    }
    if(root->left) {
        helper(root->left, sum, cur);
        cur = cur >> 1;
    }
    if(root->right) {
        helper(root->right, sum, cur);
        cur = cur >> 1;
    }
}
int sumRootToLeaf(TreeNode* root) {
    int sum{0}, cur{0};
    helper(root, sum, cur);
        
    return sum;
}

236. Lowest Common Ancestor of a Binary Tree(Medium)

給你一個binary tree和兩個node(p, q)。找出p, q共同最低的祖先node。

1. 如果root為共同的祖先，則可以在左半邊和右半邊找到p或q。

2. 如果root不為共同祖先，則只會在一邊找到p和q，另一邊找不到。那就往non-null的那邊繼續找。

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    // 找到p或q, return node
    if(!root || root == p || root == q) return root;
    // 左邊是否有p或q
    TreeNode *left = lowestCommonAncestor(root->left, p, q);
    // 右邊是否有p或q
    TreeNode *right = lowestCommonAncestor(root->right, p, q);
    // 左右邊都有，所以這是共同的root
    if(left && right) return root;
    // 否則選有的那一邊
    return left ? left : right;
}

2022/07/05

1. 為什麼這題是使用post-order?
2. 因為我必須先知道child的狀態，才可以決定parent是不是LCA。

2024/02/09
還是參考了之前的解答。

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    if(!root || root == p || root == q) return root; // child狀態
    TreeNode* l = lowestCommonAncestor(root->left, p, q); 
    TreeNode* r = lowestCommonAncestor(root->right, p, q);
    // 得到兩邊child狀態之後再來判斷
    if(l && r) return root;
    else return l ? l : r;
}

968. Binary Tree Cameras

一台camera可以看到自己和上下的node，試問最少的camera可以覆蓋所有的node。

1. 一個node有三種狀態，放置camera，有被camera監視，沒有被camera監視。
2. 如果top-down，就必須考慮node的所有可能，還要根據root node狀態推斷child node可能的狀態，比較困難。
3. 如果bottom-up的話，因為bottom狀態確定了，比較容易推斷root node的狀態，所以使用bottom-up。
4. 既然是bottom-up，就是post-order，先走訪到最底部才開始判斷前一個的狀態。

class Solution {
    enum state {mon, nomon, camera};
    int cnt;
    int helper(TreeNode *root) {
        if(!root) return mon;       // 把null node視為monitor node，因為不用管他
        int l = helper(root->left);
        int r = helper(root->right);
        if(l == nomon || r == nomon) { // child有一個沒被monitor, 放置camera, case1
            cnt++;
            return camera;
        } else if(l == mon && r == mon) // case2
            return nomon;
         return mon;                    // child 有一個有camera, case 3
        // left, right
        // mon, mon         case 2, leaf
        // mon, nomon       case 1
        // mon, camera      case 3
        // nomon, mon       case 1
        // nomon, nomon     case 1
        // nomon, camera    case 1
        // camera, mon      case 3
        // camera, nomon    case 1
        // camera, camera   case 3
    }
public:
    int minCameraCover(TreeNode* root) {
        int val = helper(root);
        return (val == nomon ? 1 : 0) + cnt; // 因為root沒被monitor，所以放置一個camera
        // time complexity  : O(N)
        // space complexity : O(N)
    }
}; 

199. Binary Tree Right Side View(Medium)

列出一個binary tree每個level最右邊node的數值。

1. 使用preorder traversal，但是先走訪右邊再走訪左邊。因為我們想要先拿到右邊的node。
2. 使用level來記錄目前走到的level，因為每一層只有一個right-most node，所以當rtn.size() < level我們才紀錄。

class Solution {
    void helper(TreeNode *root, int level, vector<int>& rtn) {
        if(!root) return;
        if(rtn.size() < level) rtn.push_back(root->val);
        helper(root->right, level + 1, rtn);
        helper(root->left, level + 1, rtn);
    }
public:
    vector<int> rightSideView(TreeNode* root) {
        vector<int> rtn;
        helper(root, 1, rtn);
        return rtn;
    }
};

110. Balanced Binary Tree

判斷binary tree是否為balanced。balanced的定義為從root來看左子樹和右子樹的高度差不為1。

1. 因為要先知道左右兩邊的高度，所以為post-order。
2. 得到兩邊子樹的高度之後，如果不是balanced那就不需要再判斷直接回傳-1。
3. 如果兩邊差大於1也是回傳-1。
4. 最後回傳計算後的高度。

int helper(TreeNode *root) {
    if(!root) return 0;
    int hofl = helper(root->left);
    int hofr = helper(root->right);
    if(hofl == -1 || hofr == -1 || abs(hofl - hofr) > 1) return -1;
    return max(hofl, hofr) + 1;
}
bool isBalanced(TreeNode* root) {
    return helper(root) == -1 ? false : true;
}

437. Path Sum III

找到在binary tree中的path剛好總合為target。這邊的path的定義是從parent到child。不會有child->parent->child的路徑。

1. 每個node都可以為起始點，所以使用line 13, line 14，把path總和算是每個node的起點。
2. 使用helper來計算以root為起點的path總和。
3. 在helper中經過的每個node都為終點，所以計算總合。line 3。
4. 如果以這個點的總和為target則加1，line 4。
5. 繼續統計以root->left和root->right為終點的path。line 5,6。
6. 因為有line 13, 14，所以不必計算單點是否等於target。

int helper(TreeNode *root, long pre) {
    if(!root) return 0;
    long cur = pre + root->val;
    return (cur == target) + 
        helper(root->left, cur) + 
        helper(root->right, cur); 
}
int target;
int pathSum(TreeNode* root, int targetSum) {
    if(!root) return 0;
    target = targetSum;
    return helper(root, 0) + 
        pathSum(root->left, targetSum) + // 從 root->left開始，所以不用判斷每個點是否為traget
        pathSum(root->right, targetSum); // 從 root->right開始
}

2246. Longest Path With Different Adjacent Characters

找出tree中，最長的path其中每兩個相鄰的node的char都不一樣。

1. 一開始使用了DFS結果TLE。
2. 參考了lee215大的解法，發現這題和124. Binary Tree Maximum Path Sum蠻像的。
3. 應該說只要是在tree中找path應該都是一樣的套路。
4. path至少會有一個node，
5. 兩個以上的node就是會跟child連在一起。
6. 有可能跟一個child連在一起，也有可能跟兩個child連在一起。
7. 如果是跟兩個child連在一起。那一定是最長的兩個child。
8. why preorder? 因為必須先知道每個child最長的path。
9. 根據s[cur] != s[child]，才可以判斷要不要取用這條path。所以判斷必須在pre-order之後。
10. 回傳只能傳回node + 最長的child。

class Solution {
    // why pre-order?
    // 因為必須先知道每個child的最長path，
    // 根據s[cur] != s[child]，才可以判斷可不可以取用這條path，
    // 必須取出兩條最長的child path就可以拼成更長的Path
    int maxans{0};
    int dfs(unordered_map<int, vector<int>>& m, int cur, string& s, int len) {
        int big1{0}, big2{0};
        for(auto& child : m[cur]) {
            int rtn = dfs(m, child, s, len + 1); // 從目前node往下的path長度
            if(s[cur] == s[child]) continue;
            if(rtn > big2) big2 = rtn;
            if(big2 > big1) swap(big1, big2);
        }
        maxans = max(maxans, big1 + big2 + 1); // 經過node最長的path由node和兩個最長的邊組成
        return big1 + 1; // 最長一條path
    }
public:
    int longestPath(vector<int>& parent, string s) {
        unordered_map<int, vector<int>> m; // node, adj node
        for(int i = 1; i < parent.size(); ++i)
            m[parent[i]].push_back(i);

        dfs(m, 0, s, 0);
        return maxans;
    }
};

958. Check Completeness of a Binary Tree

給你一個TreeNode* root，試判斷是否為complete binary tree。

1. 一開始一直在想到底是要用pre-order, in-order或是post-order，就是忘了想用level order。
2. 另一個解法是把每個node都給上一個value，最後排序這個vector但是會int overflow。
3. 根據 complete binary tree的特性，如果我用level order traversal，就不會在node之前先遇到nullptr。
4. 如果是complete binary tree最後的queue內容都會是nullptr。

bool isCompleteTree(TreeNode* root) {
    queue<TreeNode*> q{{root}};
    // 遇到nullptr就停止。
    while(q.front() != nullptr) { 
        TreeNode* cur = q.front(); q.pop();
        q.push(cur->left);
        q.push(cur->right);
    }
    
    // 如果是complete binary tree的話，最後都會是nullptr
    while(!q.empty() && q.front() == nullptr) q.pop(); 
    return q.empty();
}

979. Distribute Coins in Binary Tree

binary tree中每個node都有不同的coins，找出最少的移動可以使每個node都有一個coin。

1. 參考官方解答。
2. why post-order traversal?
   • 必須知道需要往child移動多少的coins，或是必須知道要從child移動多少coins上來parent。
   • 正數表示child有多的coins必須移動上來。
   • 負數表示child有少，必須從parent動到child。
3. 因為child移動到child都要經過parent，所以可以視為多的先從child移動到parent，parent再分配給child。
4. 也就是parent是一個中央統籌單位，多的coins先交給中央parent，再由中央parent分配給不夠的child。
5. 如果整體來說還是不夠，中央parent再跟更上面的parent要求更多的coins。
6. 如果分配完了還有多出來，中央parent再把剩下的往更上的parent繳交出去。

class Solution {
    int ans{};
    // child多的coin，必須從child移動到root
    // child缺的coin, 必須從root移動到child
    int dfs(TreeNode* root) { // + : child->root, - : root->child
        if(!root) return 0;
        int l = dfs(root->left);
        int r = dfs(root->right);
        ans += abs(l) + abs(r);
        return root->val + l + r - 1;
    }
public:
    int distributeCoins(TreeNode* root) {
        dfs(root);
        return ans;
    }
};

2477. Minimum Fuel Cost to Report To the Capital

每個node除了0之外，都要往node 0前進，每前進一個node需要1L fuel。一台車子最多有seats個椅子。試問，最少的fuel來讓所有的node都達到node 0。

1. 如果有n個人，則需要多少台車子? 使用無條件進位ceil。

ceil(n / s);

2. 所以使用post-order，因為要到達最後的leaf node，再往node 0前進，推算有多少個node在後面。
3. 使用vector<int> vis來記錄訪問過的node。
4. 為什麼統計每個node的車子數，就是統計需要的fuel?

class Solution {
    unordered_map<int, vector<int>> adj;
    vector<int> vis; // 使用visited array來避免重複走
    long long ans;
    int dfs(int n, int s) { 
        vis[n] = 1;
        int count = 1;
        //統計從child過來的node有多少個
        for(auto& nxt : adj[n]) {
            if(!vis[nxt])
                count += dfs(nxt, s);
        }
        if(n != 0)
            ans += ceil((double)count / s); //站在每個node，會有幾台車經過
            // ans += ((rtn + seats - 1) / seats);
            // 不使用ceil的無條件進位
        return count; // 有多少個node
    }
public:
    long long minimumFuelCost(vector<vector<int>>& roads, int seats) {
        for(auto& r : roads) {
            adj[r[0]].push_back(r[1]);
            adj[r[1]].push_back(r[0]);
        }
        vis.resize(roads.size() + 1);
        dfs(0, seats);
        return ans;
    }
};

tags: leetcode 刷題