---
tags: cryptography, elliptic curves
---

# Elliptic Curve Cryptography

Summary of [Andrea Corbellini](https://andrea.corbellini.name/about/)'s blog series [_ECC: A gentle introduction_](https://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/).


## Introduction

### Elliptic Curves

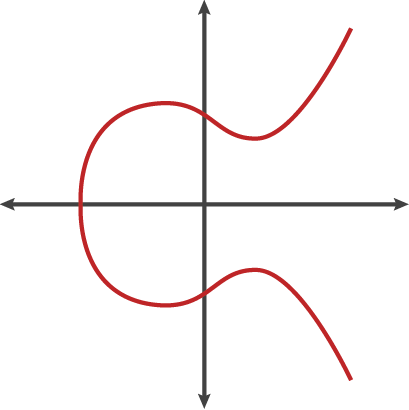
The __set of points__ described by the equation:

$y^2 = x^3 + ax + b$

where $4a^3 + 27b^2 \neq 0$ (required to exlude _singular curves_).

Equation above is called _Weierstrass normal form_.

Need __point at infinity__ (_ideal point_) to be part of curve, denoted as $0$.

Therefore, an elliptice curve is defined as:

$\{(x, y) \in \mathbb{R} \textit{ | } y^2 = x^3 + ax + b \textit{, } 4a^3 + 27b^2 \neq 0\} \cup \{0\}$

### Groups

A set ($\mathbb{G}$) for which a binary operation (denoted as $+$) is defined that respects the following four properties:
1. __closure__: $a, b \in \mathbb{G} \rightarrow a+b \in \mathbb{G}$
2. __associativity__: $(a+b)+c = a+(b+c)$
3. __identity element__ ($0$) exists such that $a+0=0+a=a$
4. __inverse__ exists for each $a \in \mathbb{G}$, such that $a+a_{inverse}=0$

A group is called *abelian group* if a fifth property is respected:

5. __commutativity__: $a+b=b+a$

The cardinality of the set is called the _order of the group_.

### Define a Group over Elliptic Curves

- Elements of group are the points of the elliptic curve
- __Identity element__ is the point at infinity ($0$)
- __Inverse__ of a point is the one symmetric about the $x$-axis
- Remember that elliptic curves are symmetric about $x$-axis
- __Addition__ is given by: _given three aligned, non-zero points $P$, $Q$, and $R$, their sum is $P+Q+R=0$
- $\rightarrow P+(Q+R)=Q+(P+R)=...=0$
- $\rightarrow$ Group is an **abelian group**


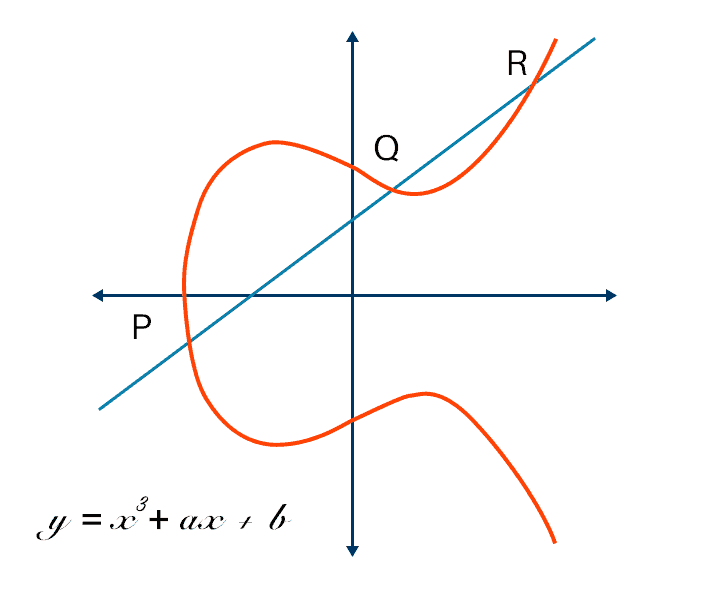
### Geometric Addition

Due to being an *abelian group*: $P+Q+R=0 \leftrightarrow P+Q=-R$.

$-R$ is the inverse of the point $R$, which is crossed in the line passing through $P$ and $Q$.


What if:
- $P=0$ or $Q=0$?
- $0$ is defined as identity, therefore $P+0=P$ and $Q+0=Q$, for any $P$ or $Q$
- $P=-Q$?
- Line through the two points is vertical, and does not intersect any third
- If $P=-Q \rightarrow P+Q=(-Q)+Q=0$ per definition

### Scalar Multiplication

How to compute $n * P$ where $n$ is a natural number?

Using [_double and add_](https://en.wikipedia.org/wiki/Elliptic_curve_point_multiplication#Double-and-add) algorithm, computation needs less than $n$ additions.

Note that there are faster algorithms.

### Logarithm Problem

Find $n$ such that $Q = nP$ for known $Q$ and $P$.

Note that this is actually a division problem, but called logarithm problem for conformity with other cryptosystems.

## Finite Fields and Discrete Logarithm

A finite field is a set with a finite number of elements with two binary operations: addition ($+$) and multiplication ($*$).

Both operations are closed, associative and commutative.
For both operations exist a unique identity element, and for every element a unique inverse element.
Also, multiplication is distributive over addition: $x*(y+z) = x*y + x*z$.

### Elliptic Curves in $\mathbb{F}_p$

$\mathbb{F}_p$ is the finite field of integers modulo $p$, where $p$ is a prime number.
$\rightarrow$ $\mathbb{F}_p$ consists of the integers from $0$ to $p-1$.

The set of points of elliptic curves in $\mathbb{F}_p$ is:
$\{(x, y) \in (\mathbb{F}_p)^2 \textit{ | }
\begin{align}
&y^2 \equiv x^3 + ax + b \pmod p, \\
&4a^3 + 27b^2 \not\equiv 0 \pmod p
\end{align} \}
\cup \{0\}$

where $0$ is point at infinity and $a, b \in \mathbb{F}_p$.

Note that elliptic curves in $\mathbb{F}_p$ are an _abelian group_.

### Order of an Elliptic Curve Group

Whats the number of points in an elliptic curve group, i.e. the order of the group?

No idea, but the [_Schoof algorithm_](https://en.wikipedia.org/wiki/Schoof%27s_algorithm) computes the order in polynomial time.

Note, that the _Schoof algorithm_ can only be used on whole elliptic curves, not subgroups.

### Scalar Multiplication and Cyclic Subgroups

Due to modular arithmetic: $nP = (n \mod p)P$.
$\rightarrow$ The result of multiplications repeat cyclically.

The set of these results, i.e. the set of multiples of $P$ is a __cyclic subgroup__ of the group formed by the elliptic curve.

A _subgroup_ is a group which is a subset of another group.
A _cyclic subgroup_ is a subgroup which elements are repeating cyclically.

The Point $P$ is called __generator__ or __base point__ of the cyclic subgroup.

### Order of a Cyclic Subgroup

How to compute the order of a subgroup generated by point $P$?
$=$ How to compute the order of $P$?

1. The order of $P$ is the smallest positive integer $n$ such that $nP = 0$
- Note that $n$ with $nP = 0$ starts a "new cycle"
2. [Lagrange's theorem](https://en.wikipedia.org/wiki/Lagrange%27s_theorem_(group_theory)) states that __the order of a subgroup is a divisor of the order of the parent group__
- If group contains $N$ points and one of its subgroups containt $n$ points, then $n$ is a divisor of $N$.

$\rightarrow$ Compute order of subgroup by:
1. Compute elliptic curve's order $N$ using _Schoof's algorithm_.
2. Find all divisors of $N$.
3. For every divisor $n$ of $N$, compute $nP$
4. The smallest $n$ such that $nP = 0$ is the order of the subgroup

### Cofactor of a Subgroup

The number $h$, with $h = N/n$ for $N$ being the order of the group and $n$ the order of the subgroup, is called the _cofactor of the subgroup_.

Note that $h$ is always an integer.

### Finding a Generator

Want:
- subgroups with high order
- order of subgroup ($n$) must be prime number

Algorithm:
1. Compute order $N$ of elliptic curve.
2. Choose order $n$ of the subgroup. Note that $n$ must be a prime number.
3. Copmute cofactor $h = N/n$.
4. Choose random point $P$ on the curve.
5. Compute $G = hP$
- Note that $G = hP$ generates a subgroup of order $n$ iff $G = hP \neq 0$.

### Discrete Logarithm Problem (for Elliptic Curves)

Find $k$ such that $Q = kP$ for known $Q$ and $P$.

Remember the normal discrete logarithm problem: Find $k$ such that $b = a^k \mod p$ for known $a$ and $b$.

## ECDH and ECDSA

### Domain Parameters

ECDH and ECDSA work in a cyclic subgroup of an elliptic curve over a finite field.

The following parameters are therefore needed:
- The __prime__ $p$ that specifies the size of the finit field.
- The __coefficients__ $a$ and $b$ of the elliptic curve equation.
- The __generator__ $G$ that generates the subgroup.
- The __order__ $n$ of the subgroup
- The __cofactor__ $h$ of the subgroup

### Elliptic Curve Cryptography

- __private key__ is a random integer $d \in \{1, ..., n-1\}$, where $n$ is the order of the subgroup.
- __public key__ is the point $H = dG$, where $G$ is the generator of the subgroup.

Knowing $d$ and $G$ its easy to compute $H$.
Knowing $H$ and $G$, its hard top compute $d$, because it requires solving the discrete logarithm problem.

### ECDH

ECDH is a variant of the [Diffie-Hellman algorithm](https://en.wikipedia.org/wiki/Diffie%E2%80%93Hellman_key_exchange) for elliptic curves.

ECDH is a _key-agreement protocol_. It enables participants to create a shared secret from which a symmetric encryption key can be constructed.

Algorithm:
1. Alice and Bob generate their private and public keys given some _domain parameters_.
- Alice has private key $d_A$ and public key $H_A = d_A G$.
- Bob has private key $d_B$ and public key $H_B = d_B G$.
2. Alice and Bob exchange their public keys over an __insecure__ channel.
- A man in the middle could intercept $H_A$ and $H_B$, but won't be able to get $d_A$ oder $d_B$ "easily".
3. Alice computes $S = d_A H_B$ and Bob computes $S = d_B H_A$ using their private keys
- Note that $S = d_A H_B = d_A (d_B G) = d_B (d_A G) = d_b H_A$

Alice and Bob now have a shared secret $S$ from which they can construct a symmetric encryption key.

#### Ephemeral ECDH

In ECDH**E**, the keys exchanges are temporary.

### ECDSA

ECDSA is a variant of the [Digital Signature Algorithm](https://en.wikipedia.org/wiki/Digital_Signature_Algorithm) applied to elliptic curves.

Via ECDSA, Alice can sign a message with her private key ($d_A$), and others can validate the signature using Alice's public key ($H_A$).

ECDSA works on the __hash__ of the message, rather than on the message itself. The hash must be __truncated__ so that the bit length of the hash equals the bit length of $n$ (the order of the subgroup).

The truncated hash is an integer, denoted as $z$.

#### Signature Generation

1. Take a __random integer__ $k \in \{1, ..., n-1\}$.
- where $n$ is the subgroup order.
2. Compute a point $P = kG$.
- where $G$ is the subgroup's generator.
3. Compute the number $r = x_p \mod n$.
- where $x_p$ is the $x$ coordinate of $P$.
4. If $r = 0$, choose different $k$ and try again.
5. Compute $s = k^{-1} (z+rd_A) \mod n$.
- where:
- $d_A$ is Alice's private key.
- $k^{-1}$ is the multiplicative inverse of $k$ modulo $n$.
- $z$ is the truncated message's hash.
6. If $s = 0$, choose different $k$ and try again.

The pair $(r, s)$ __is the signature__.

To summarize: The algorithm first generates a secret ($k$), which is hidden in $r$ thanks to point multiplication, i.e. discrete logarithm problem.
Afterwards, $r$ is bound to the message's hash via the computation of $s$.

#### Signature Verification

1. Compute integer $u_1 = s^{-1}z \mod n$.
2. Compute integer $u_2 = s^{-1}r \mod n$.
3. Compute point $P = u_1G+u_2H_A$.

Signature is valid iff $r = x_p \mod n$.

#### Importance of $k$

It is of utmost importance to keep $k$ secret, and never use a chosen $k$ for multiple signatures.
Otherwise, the private key can be extracted!