# Term project: Optimize 2D line drawing for RV32IM using fixed-point arithmetic
###### tags: `computer-arch`, `jserv`
- [Reference source code](https://github.com/sysprog21/rv32emu/blob/master/tests/line.c)
- [commit 033312c](https://github.com/sysprog21/rv32emu/commit/033312c2470c27120ddb11c77b68894e3f1ba19e)
> This project is integrated in RISC-V instruction simulator [rv32emu](https://github.com/sysprog21/rv32emu)
## Objective of the project
In this project, several knowledge will be mentioned, I will try to explain these computer science concept and give the examples.
- What is **fixed-point**, and the difference between it and floating point.
- How to implement **basic arithmetic of fixed-point**.
- How computer draw a line? though it seems a simple problem, depends on humans demands of better picture quality, this question may be even tricky than we think.
Last but not least, optimize the perfornmence of 2D line drawing executing on RV32IM, by **replacing floating point arithmetic with fixed-point arithmetic** counterpart.
## Preparation
### Previous practice in [Lab2](https://hackmd.io/@maromaSamsa/rJFkoUiNj)
In this project, practicing how to generate an **ELF(executable and Linkable Format)** file by using **GNU Toolchain for RISC-V**, and execute the program on rv32emu, a RISC-V instruction set based emulator.
### Floating point regulation in C: [IEEE 754](https://en.wikipedia.org/wiki/IEEE_754)
For the purpose of representing decimal points in computer, floating point is one of the method, **IEEE 754** is commonly used in modern.
The data space of the standard part will be used to store the position of the decimal point. Since the decimal point is not fixed, it is called `floating point`.
In IEEE 754 format, a 32-bit, single precise floating point's value would be present as follow:
$Value = sign * (1.F)_{binary} * 2^{EXP - bias}$
`1` in this formula represents the first significant bit, it is called `hidden bit`, since it do not have to store in the data space.
| Sign | Exp | F |
| -------- | -------- | -------- |
| 1 bit | 8 bits | 23 bits |
$bias = 2^7 - 1 = 127$, *hence the origin of* $(Exp - bias)$ *would at* `0`.
Discussing about data type `float` in C, which follows by IEEE 754 32-bit single precision format.
```c
// 0b0_01111111_00100000000000000000000
uint32_t a = 0x3f900000;
float *b = &a;
int bias = (1 << 7) -1;
int sign = a >> 31;
int offset = ((a & 0x7f800000) >> 23) - bias;
int fraction = a & 0x007fffff;
printf("sign: %c\n", sign? '-' : '+');
printf("offset: %d\n", offset);
printf("fraction: 0x%x\n", fraction);
printf("IEEE 754: %a\n", *b);
printf("value: %f\n", *b);
```
The output would be:
```
sign: +
offset: 0
fraction: 0x100000
IEEE 754: 0x1.2p+0 // 0b1.001 * 2^0
value: 1.125000
```
There is an online [IEEE 754 converter](https://www.h-schmidt.net/FloatConverter/IEEE754.html), provide us with a convenient way to verify how various values are stored in IEEE 754.
## Fixed point
Compared with floating point, the representation method of fixed point number is more intuitive. If the range of values to be calculated is known in advance and limited to a smaller range, fixed-point arithmetic can effectively use its bits.
Take 32-bit data space for example:
```c
// we defined the lowest 3 bits represent decimal point.
uint8_t a = 0b01011001 // seen as 0b01011.001
printf("integer: %d\n", a >> 3);
printf("decimal point: %f\n", (float)a / (1<<3));
```
```
integer: 11
decimal point: 11.125000
```
Since the position of the decimal point is fixed, the **`interval`** between all the representable value is also fixed. take previous example to expalen:
```
0b01011.001
```
**0b0.001** is the smallest interval between the values, that is, 0.125 ($2^{-3}$), usually the fixed-point number will pre-determine how many digits to use to represent the decimal point, then scale according to the situation.
In essence, fixed-point numbers are an integer data structure, which means that they can just perform fast calculations by using general ALU, without using floating-point operators.
### Fixed point regulation: [Q format](https://en.wikipedia.org/wiki/Q_(number_format))
Since the fixed-point number itself does not record the bits of the decimal point position, we can use the Q format to formulate the rules in the begining.
For 32-bit signed fixed point, The Q format can be written as **Qm.n**:
| sign bit | integer bits | decimal bits |
| -------- | -------- | -------- |
| **1** | **m** | **n** |
$Where$ $m + n = 31$
For 32-bit unsigned fixed point, The Q format can be written as **UQm.n**:
| integer bits | decimal bits |
| -------- | -------- |
| **m** | **n** |
$Where$ $m + n = 32$
For their fixed precision we can give an mathmetical expression by **n**:
$precision = 2^{-n}$
## Fixed piont Arithmetic
:::success
I have implemented those important fixed point algorithms for this project, please check custom library [**qformat.h**](https://github.com/maromaSamsa/Computer_Arch2022/blob/main/TermProject/line/qformat.h) for souce code
:::
$let$ $N$ $be$ $any$ $Qm.n$ $fixed$ $point$, $N \in \mathbb{Z}$
$let$ $1/d$ $be$ $its$ $precision$ $2^{-n}$.
$N/d$ is fixed point value.
:::success
We can think of fixed-point numbers as integers "scaled by $1/d$ times"
:::
### Conversion between floating and fixed point
$let$ $F$ $be$ $any$ $floating$ $point$ $value$.
$\because$ $F = N/d = N*2^{-n}$
$\therefore$ $N = F*d = F*2^{n}$
```c
// define Q is bits count for representing decimal point
// q_fmt: 32-bit Q format fixed piont
/* format convertion: float to Q format */
#define f2Q(x) ((q_fmt)((x)*(1<<Q)))
/* format convertion: Q format to float */
#define Q2f(x) (((float)(x))/(1<<Q))
```
### Add
Suppose two of the fixed point precesion are both $1/d$:
$N_1/d + N_2/d = \frac{N_1 + N_2}{d} = N_3/d$
$\therefore N_3 = N_1 + N_2$
In add arithmetic, precision wouldn't change after compute, just directly add up two numbers and check overflow.
```c
/* addition of Q format value*/
// q_buf: 64-bit Q format fixed piont, as the buffer in operation
// QFMT_MAX: 0x7FFFFFFF
// QFMT_MIN: 0x80000000
static inline q_fmt q_add(q_fmt a, q_fmt b)
{
q_buf tmp = (q_buf)a + (q_buf)b;
// check overflow
if(tmp > (q_buf)QFMT_MAX) return (q_fmt)QFMT_MAX;
if(tmp * -1 >= (q_buf)QFMT_MIN) return (q_fmt)QFMT_MIN;
return (q_fmt)tmp;
};
```
Since we use the highest bit of the value to represent the sign, we don't need to implement the **subtraction**.
### Multiply
$N_1/d * N_2/d = \frac{N_1*N_2}{d^2} = N_3/d$
$\therefore N_3 = N_1 * N_2 * 1/d = N_1 * N_2 * 2^{-n}$
Multiplication results in **double precision**, we need to maintain the scaling factor $1/d$ back to **single precision**.
Because the denominator is a power of two, multiplication by a power of two can be expressed as a left shift `<< n` in binary, and division by a power of two can be expressed as a right shift `>> n` in binary
before rescale the precision we can also concern about rounding, since for every adjacent bit they differ from each other **by a factor of two**, simply adding one to the n-1th bit can affect the nth bit with rounding logic.
```c
/* multiplication of Q format value */
static inline q_fmt q_mul(q_fmt a, q_fmt b)
{
q_buf tmp = (q_buf)a * (q_buf)b;
// rounding and rescale precision
tmp += 1 << (Q-1); // tmp is still at double precision 2^(-2Q)
tmp >>= Q; // back to single precision 2^(-Q)
// check overflow
if(tmp > (q_buf)QFMT_MAX) return (q_fmt)QFMT_MAX;
if(tmp * -1 >= (q_buf)QFMT_MIN) return (q_fmt)QFMT_MIN;
return (q_fmt)tmp;
}
```
### Division
:::success
Considering the operational efficiency, generally, the division operation will not be used as much as possible. For the need to divide by a power of 2, the right shift operation is very practical `>> 1`.
:::
$N_1/d * d/N_2 = N_1 / N_2 = N_3 / d$
$\therefore N_3 = \frac {N_1*d}{N_2} = N_1 * 2^{n} / N_2$
```c
/* division of Q format value */
static inline q_fmt q_div(q_fmt a, q_fmt b)
{
q_buf tmp = (q_buf)a << Q;
if ((tmp >= 0 && b >= 0) || (tmp < 0 && b < 0)) {
tmp += (b >> 1);
} else {
tmp -= (b >> 1);
}
return (q_fmt)(tmp / b);
}
```
## Compare with floating point in rv32emu
To verify the performance difference between floating point arithmetic and fixed point arithmetic, in this session I write several simple program to test each arithmetic (`+`, `*`, `/`).
In order to obtain information about the CPU, three sets of RISC-V pseudo-instructions are introduced in [The RISC-V Instruction Set Manual: 10.1 Base Counters and Timers](https://riscv.org/wp-content/uploads/2019/06/riscv-spec.pdf):

### How to use
```c
// in RISC-V Assembly code .s
RDCYCLE [rd1]
...
// target program
...
RDCYCLE [rd2]
// cpu cycle count of the program = rd2 - rd1 - 1
```
### `RDCYCLE` and `RDCYCLEH`: CPU cycle counter
> The `RDCYCLE` pseudoinstruction reads the low XLEN bits of the cycle CSR which holds a count of the number of clock cycles executed by the processor core on which the hart is running from an arbitrary start time in the past.
>
> `RDCYCLEH` is an RV32I instruction that reads bits 63–32 of the same cycle counter
### `RDTIME` and `RDTIMEH`: timer
> The `RDTIME` pseudoinstruction reads the low XLEN bits of the time CSR, which counts wall-clock real time that has passed from an arbitrary start time in the past.
>
> `RDTIMEH` is an RV32I-only instruction that reads bits 63–32 of the same real-time counter
### `RDINSTRET` and `RDINSTRETH`: instruction counter
> The `RDINSTRET` pseudoinstruction reads the low XLEN bits of the instret CSR, which counts the number of instructions retired by this hart from some arbitrary start point in the past.
>
> `RDINSTRETH` is an RV32I-only instruction that reads bits 63–32 of the same instruction counter.
Testing program is a for loop repeat 1000 times specific arithmetic, take addition for instance:
```c=\
// test.c
float a = 900;
float b = M_PI; // 3.1415926...
q_fmt c = (900 << Q);
q_fmt d = PI_Q; // 1686629713>>(29-Q)
// testing floating arithmetic
for(int i = 0; i < 1000; ++i){
a -= b;
}
// testing fixed arithmetic
for(int i = 0; i < 1000; ++i){
c = q_add(c, -d);
}
```
Just for testing, disable optimization lable.
```shell
riscv-none-elf-gcc -march=rv32i -mabi=ilp32 -O0 -o test.s -S test.c
riscv-none-elf-gcc -march=rv32i -mabi=ilp32 -o compare.elf test.s
```
In `test.s`, insert these pseudo-instructions to get related information.
:::success
Though it seems straightforward of floating minus operation in C code, in `test.s`, I found that floating arithmetic function call.
```c
lw a1,-36(s0)
lw a0,-20(s0)
call __subsf3
```
:::
Finally, run `compare.elf` in rv32emu.
```shell
$ build/rv32emu compare.elf
```
- Add test
| Count | Float | Fixed |
| -------- | -------- | -------- |
| CYCLE | 67250 | **46477** |
| TIME | 6890 | **4492** |
| INSTR | 67115 | **46594** |
- Multiply test
| Count | Float | Fixed |
| -------- | -------- | -------- |
| CYCLE | 281550 | **229716** |
| TIME | 48534 | **22477** |
| INSTR | 281685 | **229806** |
- Division test
| Count | Float | Fixed |
| -------- | -------- | -------- |
| CYCLE | 513897 | **464903** |
| TIME | 63314 | **46907** |
| INSTR | 514032 | **465011** |
:::warning
I am not sure what is the unit of time:
| Clock rate (CYCLE/TIME) | Float | Fixed |
| -------------------------- | -------- | -------- |
| Add | 9.761 | 10.347 |
| Mul | 5.801 | 10.220 |
| Div | 8.117 | 9.911 |
The reason why $Rate_{fixed} > Rate_{float}$ is uncertain, perhaps this indicates that the critical path between FPU pipelines has a larger delay time?
| CPI (CYCLE/INSTR) | Float | Fixed |
| -------------------- | -------- | -------- |
| Add | 1.002 | 0.997 |
| Mul | 1.000 | 1.000 |
| Div | 1.000 | 1.000 |
:::
## Rewrite `line.c` to fixed-point arithmetic, and compare
After adjusting the parameter `Q` in [`qformat.h`](https://github.com/maromaSamsa/Computer_Arch2022/blob/main/TermProject/line/qformat.h), it is found that [`line.c`](https://github.com/maromaSamsa/Computer_Arch2022/blob/main/TermProject/line/line.c) can use fixed-point numbers in the highest **Q11.20** format for operations without overflow.
### Compare images drawn with fixed-point numbers at different precisions
- **The result of the original floating-point arithmetic**

- **Q27.4**

- **Q25.6**

- **Q23.8**

- **Q17.10**

- **Q11.20**

- **Q9.22 (overflow occur)**

### Rewrite from math.h to support fixed point
In addition to the basic arithmetic operations, other arithmetic methods also need to be implemented.
- floor
```c
/* return the largest integral value that is not greater than x */
static inline q_fmt floorq(q_fmt x)
{
q_fmt mask = (0xFFFFFFFF >> Q) << Q;
return x & mask;
}
```
- ceil
```c
/* return the smallest integral value that is not less than x */
static inline q_fmt ceilq(q_fmt x)
{
q_fmt mask = (0xFFFFFFFF >> Q) << Q;
q_fmt delta = x & ~mask;
x = x & mask;
return delta? q_add(x, 1<<Q): x;
}
```
- sqrt
```c
static inline q_fmt sqrtq(q_fmt x)
{
q_fmt res = 0;
q_fmt bit = 1<<15;
// shift bit to the highest bit 1' in x
while(bit > x){
bit >>= 1;
}
for(bit; bit > 0; bit >>= 1){
int tmp = bit + res;
// check overflow: 46341^2 > 2^31 - 1, which is the maximun value
if(tmp > 46340) continue;
int square = tmp*tmp;
if(square < x){
res = tmp;
}
if(square == x) return tmp;
// iter: goto next lower bit to get more precise sqrt value
}
return res << (Q/2); // **this would waste Q/2 bits precision.
}
```
:::success
Previous operation would waste Q/2 bits precision. Because I'm shifting left before passing back.

Therefore I fixed the code, and try to avoid the use of 64-bit buffer.
```c
/* return the nonnegative square root of x */
static inline q_fmt sqrtq(q_fmt x)
{
if(x <= 0) return 0;
q_fmt res = 0;
q_fmt bit = 1<<15;
int offset = 0;
for(q_fmt i = x; !(0x40000000 & i); i <<= 1){
++offset;
}
offset = (offset & ~1);
x <<= offset;
// shift bit to the highest bit 1' in x
while(bit > x){
bit >>= 1;
}
for(bit; bit > 0; bit >>= 1){
int tmp = bit + res;
// check overflow: 46341^2 > 2^31 - 1, which is the maximun value
if(tmp > 46340) continue;
int square = tmp*tmp;
if(square <= x){
res = tmp;
if(square == x) break;
}
// iter: goto next lower bit to get more precise sqrt value
}
offset >>= 1;
offset -= (Q >> 1);
return (offset >= 0)? res >> offset : res << (-offset) ;
}
```
:::
- sin and cos
Because the sine and cosine values under the same radian are obtained at the same time, combination can reduce the calculation cost.
$sin(\pi/2)$ and $cos(\pi/2)$ are definite values ($0$ $and$ $1$). Use the **half-angle formula** to obtain the sine and cosine values of $\pi/8$, $\pi/16$, ..., and then use the **difference angle formula** to approximate to the target angle.
```c
static inline q_fmt cosHalf(q_fmt cosx)
{
return sqrtq((I2Q(1) + cosx) >> 1);
}
static inline q_fmt sinHalf(q_fmt cosx)
{
return sqrtq((I2Q(1) - cosx) >> 1);
}
/* get both sin and cos value in the same radius */
static inline void sinAndcos(q_fmt radius, q_fmt *sin_t, q_fmt *cos_t)
{
int region = (radius / (PI_Q >> 1)) & 0b11;
// theta must be pi/2 to 0 and start from x-axis
q_fmt theta = radius % (PI_Q >> 1);
if (region & 0b1) theta = (PI_Q >> 1) - theta;
// start from cos(pi/2) and sin(pi/2)
radius = PI_Q >> 1;
q_fmt cos_rad = 0;
q_fmt sin_rad = I2Q(1);
// start from cos(0) and sin(0)
*cos_t = I2Q(1);
*sin_t = 0;
while(radius > 0){
if(radius <= theta){
theta -= radius;
q_fmt tmp = q_mul(*cos_t, cos_rad) - q_mul(*sin_t, sin_rad);
*sin_t = q_mul(*sin_t, cos_rad) + q_mul(*cos_t, sin_rad);
*cos_t = tmp;
}
if(theta == 0) break;
radius >>= 1;
sin_rad = sinHalf(cos_rad);
cos_rad = cosHalf(cos_rad);
}
if(region == 0b10 || region == 0b01) *cos_t *= -1;
if(region & 0b10) *sin_t *= -1;
}
```
:::success
It is not precise enough to calculate the angle when close to the x and y axis:
- **Q11.20**

So I thought to myself: "Maybe sqrt has some errors when dealing with $1+\delta$", so I modified the numerical result of sqrt approximating 1 to returned 1.
```c
static inline q_fmt sqrtq(q_fmt x)
{
if(x <= 0) return 0;
if(x < I2Q(1) + (1<<(Q/2-1)) && x > I2Q(1) - (1<<(Q/2-1))) return I2Q(1);
q_fmt res = 0;
...
```
Fortunately, my guess was correct, the ouptut result is almost indistinguishable from the original image.
:::
### Compare line.c in rv32emu (Q11.20)
- **No optimize -O0**
| Count | float (origin) | Fixed (mine) |
| -------- | --------------- | ------------ |
| CYCLE | **1732706067** | 2020806114 |
| TIME | 112423500 | **76953173** |
| INSTR | **1732706209** | 2020806256 |
The execution time of the fixed-point number version is relatively short, but the number of cycles and instructions is large. I am not sure whether it is because of the need for arithmetic function calls.
- **Optimize -O1**
| Count | float (origin) | Fixed (mine) |
| -------- | --------------- | ------------ |
| CYCLE | 1652620882 | **1644796854** |
| TIME | 95192937 | **73433731** |
| INSTR | 1652621024 | **1644796996** |
After basic optimizations, fixed-point arithmetic outperforms floating-point numbers in all three.
- **Optimize -Ofast**
| Count | float (origin) | Fixed (mine) |
| -------- | --------------- | ------------ |
| CYCLE | **1058757473** | 1521690262 |
| TIME | **48471768** | 50361062 |
| INSTR | **1058757615** | 1521690404 |
Unlike expected, the fast optimized result did not outperform floating-point numbers, probably because I haven't implemented the arithmetic of `cos` and `sin` in fixed-point numbers yet (at the momemt I had not implemented them).
:::warning
Later I have checked the performance of my fixed point sqrt function, it is way too slow compared with sqrtf()
- sqrt function
| Count | Float | Fixed |
| -------- | -------- | -------- |
| CYCLE | 228442 | 462650 |
For now it is not clear to me whether there is a better algorithm for sqrt in fixed point.
READ: [從 √2 的存在談開平方根的快速運算](https://hackmd.io/@sysprog/sqrt)
:::
### The best result so far
- Turn off overflow checking (confirmed that no overflow occurred in Q11.20)
- Does not rely on any floating-point operations (including methods provided by math.h)
- -Ofast optimization
| Count | float (origin) | Fixed (mine) |
| -------- | --------------- | ------------ |
| CYCLE | **1058757473** | 1082171119 |
| TIME | 48471768 | **41783101** |
| INSTR | **1058757615** | 1082171261 |
## How computer draw a line
### [Bresenham](https://xlinux.nist.gov/dads/HTML/bresenham.html)
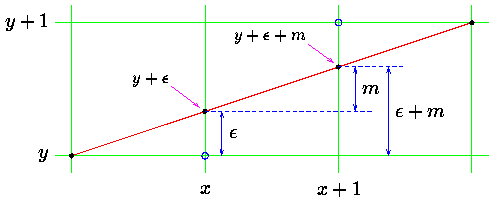
First we consider drawing a line on a raster grid where we restrict the allowable slopes of the line to the range $0 \le m \le 1$, $where\ m = \frac{dy}{dx}$.
If we further restrict the line-drawing routine so that it always increments _x_ as it plots, it becomes clear that, having plotted a point at _(x,y)_, the routine has a severely limited range of options as to where it may put the _next_ point on the line:
- It may plot the point $(x+1,\ y)$ , $or\ (x+1,\ y+1)$.
At the performance constrain, all calculation must be in integer. Since we assume that $0 \le m \le 1$, therefore in every step of the algorithm, $x$ always $+1$ toward destination In this situation, the main point of the algorithm is: **when does $y + 1?$**.
**Bresenham's algorithm** told us that for every step $1,2,3,...k$, we can define $m = \frac{dy}{dx} = \frac{k\Delta y}{\Delta x}$$(Integer)...\epsilon_k$, therefore $(x_k,y_k)$ is at position $(x_0+k,\ \frac{k\Delta y}{\Delta x} + Dcision(\epsilon_k))$.
$def\ Decision(x):$
   $return\ 1,\ if\ 2*\epsilon > 1$
   $return\ 0,\ else$
Since the real position will closer to $(x_0+k,\ \frac{k\Delta y}{\Delta x} + 1)$ when $\epsilon > 0.5 \equiv 2*\epsilon > 1$ (we only can calculate in integer)
#### Sudo Code and implement
$Draw\ a\ line\ from\ (x_0, y_0)\ to\ (x_n, y_n)$
$int\ dx = x_{n} - x_{0}$
$int\ dy = y_{n} - y_{0}$
$int\ \epsilon = 0$
$for$ $x = x_k\ to\ x_n$ $,\ x\in\mathbb{Z}$ $,\ k = 0, 1, 2,...,n$
   $x_{k+1} = x_k + 1$
   $\epsilon = \epsilon + dy$
   $if\ \epsilon*2 > dx,\ then$
     $y_{k+1} = y_{k} + 1$
     $\epsilon = \epsilon - dx$
   $else$
     $y_{k+1} = y_{k}$
   $end\ if$
$iter\ next$
Consider of all situation that $-\infty < m < \infty$, Where is the implementation in C:
```c
// Modified from https://rosettacode.org/wiki/Bitmap/Bresenham%27s_line_algorithm#C
void bresenham(int x0, int y0, int x1, int y1) {
int dx = abs(x1 - x0), sx = x0 < x1 ? 1 : -1;
int dy = abs(y1 - y0), sy = y0 < y1 ? 1 : -1;
int err = (dx > dy ? dx : -dy) >> 1;
while (x0 != x1 || y0 != y1) {
setpixel(x0, y0)
int e2 = err;
if (e2 > -dx) { err -= dy; x0 += sx; }
if (e2 < dy) { err += dx; y0 += sy; }
}
}
```
### Signed distance field (SDF)
SDF is a mathematical method used to express **the distance of the surface of the object**. It divides the object surface into two regions: **object interior and object exterior**. Distance values inside the object are **negative**, while distance values outside the object are **positive**. Such distance values are called "signed distances". SDF usually be used to render objects in 3D environment, do simulation and collision detection, etc.

**In this project, we use the concept of SDF to calculate the distance between each pixel and a given line segment**:

$\overrightarrow{AD} = \frac{\overrightarrow{AB} \cdot \overrightarrow{AC}}{|\overrightarrow{AB}|^2} \cdot \overrightarrow{AB} = k*\overrightarrow{AB}$
$\overrightarrow{CD} = \overrightarrow{AC} - \overrightarrow{AD}$
$distance = |\overrightarrow{CD}| = |\overrightarrow{AC} - k*\overrightarrow{AB}|$
Because we want the distance from the line segment instead of its straight line equation, constrain $k$ such that $0 \le k \le 1$.
```c
float capsuleSDF(float px, float py, float ax, float ay, float bx, float by, float r) {
float pax = px - ax, pay = py - ay, bax = bx - ax, bay = by - ay;
float h = fmaxf(fminf((pax * bax + pay * bay) / (bax * bax + bay * bay), 1.0f), 0.0f);
float dx = pax - bax * h, dy = pay - bay * h;
return sqrtf(dx * dx + dy * dy) - r;
}
```
> Variable `r` indicates the “sphere of influence” of the line segment. If the pixel is within this range, it will be considered as the interior of the line segment and returns **negative** distance.
#### SDF with AABB optimization
Under the axis-aligned bounding box (AABB) optimization, we only care about the SDF of the bounding box containing the line segment, and do not visit every pixel of the image every time.
```c
void lineSDFAABB(float ax, float ay, float bx, float by, float r) {
int x0 = (int)floorf(fminf(ax, bx) - r);
int x1 = (int) ceilf(fmaxf(ax, bx) + r);
int y0 = (int)floorf(fminf(ay, by) - r);
int y1 = (int) ceilf(fmaxf(ay, by) + r);
for (int y = y0; y <= y1; y++)
for (int x = x0; x <= x1; x++)
alphablend(x, y, fmaxf(fminf(0.5f - capsuleSDF(x, y, ax, ay, bx, by, r), 1.0f), 0.0f), 0.0f, 0.0f, 0.0f);
}
```