---
tags: TrRun3
id: Arrg-A28_lincomb-logic.md
---

# 檜山トレラン3 A28 小ネタ：一文字主義／線形結合と古典論理

$\newcommand{\B}{{\bf B} }
\newcommand{\Imp}{ \Rightarrow }%
\newcommand{\Iff}{\Leftrightarrow}
%$

<!--
$
%
\newcommand{\conc}{\mathop {\#}}
\newcommand{\BL}{ \{\![ }
\newcommand{\BR}{ ]\!\} }
\newcommand{\Rnn}{ {\bf R}_{\ge 0}}
\newcommand{\LCL}{ (\![ }
\newcommand{\LCR}{ ]\!) }
\newcommand{\In}{\text{ in }}%
\require{color}%
\newcommand{\Keyword}[1]{ \textcolor{green}{ \bf \text{#1} } }%
\newcommand{\For}{\Keyword{For }}%
\newcommand{\WeDefine}{\Keyword{WeDefine }}%
\newcommand{\WeWillDefine}{\Keyword{WeWillDefine }}%
\newcommand{\OmitDefinition}{\Keyword{OmitDefinition }}%
\newcommand{\Where}{\Keyword{Where }}%
\newcommand{\Sy}[1]{ \langle #1 \rangle } % symbole
\newcommand{\On}{\text{ on } }

\newcommand{\When}{\Keyword{When } }

\newcommand{\Let}{\Keyword{Let }}%

\newcommand{\WeAssert}{\Keyword{WeAssert }}%
\newcommand{\Justification}{\Keyword{Justification }}%
\newcommand{\Then}{\Keyword{Then }}%
\newcommand{\cat}[1]{\mathcal{#1}}%

\newcommand{\WeUse}{\Keyword{WeUse }}%
\newcommand{\WeAbuse}{\Keyword{WeAbuse }}%
\newcommand{\Exn}[1]{ [\!( #1 )\!] }

\newcommand{\R}{ {\bf R} }
\newcommand{\hyp}{ \text{-} }

\newcommand{\Rnni}{ {\bf R}_{\ge 0}^{+\infty}}

\newcommand{\id}{ \mathrm{id} } % id
\newcommand{\pto}{ \supseteq\!\to }
%$
-->

☆小ネタは“まくら”用
☆まくらにしては後半がボリュームあり過ぎ。たぶん適当な所で中断する。
☆話題は、数学の“独学が難しい部分”

## こんな記法に出会った

親の集合〈全体集合〉 $I$ に対する $Bag(I)$ について、


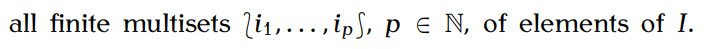
$Bag(I) = Multiset(I)$ の要素を独特な括弧で書くよ、という話（<https://arxiv.org/abs/2104.12398>）。

バッグ〈マルチセット〉の標準記法は無いから好きにしていいのだが、

- なぜ1文字（左右で2文字）の括弧記号に拘るのだろう？

プログラミング言語やマークアップ言語なら次のように書いてもいい。

Bag([a, b, c])
Bag{a, b, c}
<bag>a, b, c</bag>
\begin{bag} a, b, c \end{bag}

数学の==強迫観念的==な記法ポリシーは：

1. 変数名、演算子記号、区切り記号、囲み記号などは**1文字**にすべし。
2. 2文字以上使うヤツは死ね。
3. 長い綴りのキーワード使うヤツは地獄に落ちろ。

とにかく短く書きたいので、省略、オーバーロード、コンフリクトはやむなし。

短く簡潔に書くことは計算では絶大なメリットがあるが、読む側の解釈負担が（極端に）増大するデメリットがある。

檜山は出自が数学村ではないので、長い綴りのキーワード使うのにヤブサカではないが（例：$LinComb, Crush$）、短い書き方と逆のメリット／デメリットがある。

外部から数学村に入る人間は「一文字主義の村だ」と認識しておかないと排斥される。

## 無限和が自由に出来るとき：ブーリアン係数線形結合

全然別な話題：

本セミナー今クールの主題は線形結合、つまりスカラー倍した項の**有限和**。だが、無限和が出来ると古典論理が展開できる -- 今回の話題ではないのだが。

一般論から、

$\quad LinComb[\B](X) \cong Map_{finSupp}(X, \B) \cong FinPow(X)\\
\quad FinPow(X) := \{A\in Pow(X) \mid card(A) \le \infty\}$

有限性条件が付きまとうのは、一般的には「足し算できなくなる」から。半環 $\B$ は特殊で

1. 無限の足し算ができる。
2. 足し算と掛け算の役割をひっくり返せる（ド・モルガン双対）。

よって、

$\quad InfLinComb[\B](X) \cong Map(X, \B) \cong Pow(X)$

$InfLinComb[\B](X)$ が正体不明だが、$Map(X, \B)$ の別名〈別表記〉だと思えばよい。$Map(X, \B) \cong Pow(X)$ により、

1. 述語（ブール値の関数） ←→ 部分集合
1. 述語に対する論理演算 ←→ 部分集合に対する集合演算
1. 述語のあいだの関係 ←→ 部分集合のあいだの関係
1. 述語のメタ述語 ←→ 部分集合の述語
1. 述語の存在限量子 ←→ 部分集合の射影

残念ながら、この対応関係が正しく教えられてない（歪んでる）。以下の表は（もし知らなかったのなら）アンラーン・リラーン用に==必ず役に立つ==であろう。

==以下の表の解説で入門的セミナー1クール分になりそう。==

**述語に対する論理演算 ←→ 部分集合に対する集合演算**

| 述語 | 部分集合 |
|------|---------|
| $p\lor q$ | $A \cup B$ |
| $p \land q$ | $A \cap B$ |
| $\lnot p$ | $A^c$ |
| $p \Rightarrow q$ | $A \triangleright B$ |
| $p \Leftrightarrow q$ | $A \diamond B$ |

※ $A \triangleright B := A^c \cup B$ これは、$A$ の==Bからはみ出し部分==の補集合 $(B\setminus A )^c$
※ $A \diamond B :＝ (A\triangleright B)\cap(B\triangleright A)$ これは、$A$ と $B$ の==対称差==の補集合。対称差は「和」のことで（→[B26 名付けの無茶苦茶](https://hackmd.io/@m-hiyama/HyuP-4dXK)）、排他的ORに対応。

定数記号〈述語固有名〉：

| 述語 | 部分集合 |
|------|---------|
| $\top$ | $X$ |
| $\bot$ | $\emptyset$ |

**述語のあいだの関係 ←→ 部分集合のあいだの関係**

| 述語 | 部分集合 |
|------|---------|
| $p \models q$ | $A \subseteq B$ |
| $p \equiv q$ | $A = B$ |

※ $p \equiv q$ は $p = q$ でもいいが、$eq:X\times X \to \B$ という述語にイコール記号が使われるのでオーバーロードを避けたいだけ。
※ 最大の問題点は、**演算 $p \Rightarrow q$ と関係 $p \models q$ が混同されている**こと。理由は記号の不在とオーバーロード。
※ 集合に対して言えば、「$A \triangleright B = X$ なら $A\subseteq B$ となる」ってだけのハナシ。類似のハナシは： $n \% m = 0$ と $m \sqsubseteq n$ は同値。同値だけど、「割り算の余り」と「約数・倍数関係」は別物。
※ 論理演算 $\Imp$ に対して、小難しい哲学的議論をしている人がいるが、そもそもが論理演算と述語のあいだの関係の混同・誤解から出発していたりして、いくら難しい理屈をこねても「ハナシにならない」。

**述語のメタ述語 ←→ 部分集合の述語**

| 述語 | 部分集合 |別な書き方 |
|------|---------|-----------|
| $\models p$ | $IsTotal(A)$ | $X = A$ |
| $\not\models p$ | $\lnot IsTotal(A)$ | $X \ne A$ |
| $\models \lnot p$ | $IsTotal(A^c)$ | $X = A^c$ |
| $\not\models \lnot p$ | $\lnot IsTotal(A^c)$ | $X \ne A^c$ |

※ $IsTotal(A^c) \equiv IsEmpty(A)$
※ $Map(Map(X), \B) \cong Map(Pow(X), \B) \cong Pow(Pow(X))$ ← この対応までキチンとやればいいのもを。グジャグジャ・モヤモヤで済ませてしまう。

**述語の存在限量子 ←→ 部分集合の射影**

| 述語 | 部分集合 |
|------|---------|
| $p\in Map(X\times Y, \B)$ | $A\in Pow(X\times Y)$ |
| $\exists x.p(x, y)$ | $\pi^1(A) \in Pow(Y)$ |
| $\forall x.p(x, y)$ | $(\pi^1(A^c))^c \in Pow(Y)$ |

※ $\exists x.p(x, y) = \sum_{x\in X}p(x, y)$
※ $\forall x.p(x, y) = \prod_{x\in X}p(x, y) = \lnot \sum_{x\in X} \lnot p(x, y)$