---
tags: TrRun4
id: Theo-B02_formalDef.md
---
<style>
div.def {
border-left: 5px solid skyblue;
padding-left: 1em
}
</style>
# 檜山トレラン4 B02 名前の使用法と導入時の半形式的記述
$\newcommand{\In}{\text{ in } }
\newcommand{\On}{\text{ on } }
\newcommand{\op}{\mathrm{op} }
\newcommand{\id}{\mathrm{id} }
\newcommand{\cat}[1]{\mathcal{ #1 } }
\newcommand{\u}[1]{\underline{ #1 } }
\newcommand{\Imp}{\Rightarrow }
\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\conc}{\mathop{\#} }
\newcommand{\mrm}[1]{\mathrm{#1} }
%
\newcommand{\Id}{\mathrm{Id}}
\newcommand{\dom}{\mathrm{dom} }
\newcommand{\cod}{\mathrm{cod} }
\newcommand{\comp}{\mathrm{comp} }
%
\newcommand{\assig}{:=\!\gt }
\require{color}%
\newcommand{\Keyword}[1]{ \textcolor{green}{ \bf \text{#1} } }%
\newcommand{\For}{\Keyword{For }}%
\newcommand{\Let}{\Keyword{Let }}%
\newcommand{\WeWillDefine}{\Keyword{WeWillDefine }}%
\newcommand{\WeDefine}{\Keyword{WeDefine }}%
\newcommand{\Where}{\Keyword{Where }}%
\newcommand{\Justification}{\Keyword{Justification }}%
\newcommand{\Using}{\quad\Keyword{Using }}
\newcommand{\ChangeNotation}{\quad\Keyword{ChangeNotation }}
\newcommand{\Substitution}{\quad\Keyword{Substitution }}
\newcommand{\When}{\Keyword{When } }
\newcommand{\WeAssert}{\Keyword{WeAssert }}
\newcommand{\WeIntroduce}{\Keyword{WeIntroduce }}
\newcommand{\WeInstantiate}{\Keyword{WeInstantiate }}
\newcommand{\Requires}{\Keyword{Requires }}
\newcommand{\As}{\Keyword{ As } }
\newcommand{\IsA}{\Keyword{ IsA } }
\newcommand{\Of}{\Keyword{ Of } }
\newcommand{\ClassOf}{\Keyword{ClassOf } }
\newcommand{\Things}{\Keyword{ Things} }
%$
## 名前の使用法
[E01 名付けのジレンマ](https://hackmd.io/@m-hiyama/HJrISPEjY) で述べたように、名前(ラベルや記号も含む)が何を名指しているのか? 名前の正体は何なのか? を==常に追跡==しなくてはならない。
モノイド、群、半環、ベクトル空間などの数学的構造〈mathematical structure〉は、幾つかの構成素〈constituent \| stuff \| ingredient〉(部品、素材)から構成される。数学的構造の構成素とは、集合、写像、要素(ポインティング写像に置き換えるほうがよいが)、関係など。
ここで例え話をするが; オモチャのレゴブロックは、色やサイズの違いはあれども、素材〈構成素〉としては**ブロック**としか呼びようがない。

しかし、ブロックを素材としてワニやお馬さんという構造物を作れば、とある黄緑のブロックは「**ワニの顔**」という役割を担い、とある黄色いブロックは「**お馬さんの足**」という役割を担い、役割名で呼ばれる。

数学においても、素材〈構成素〉としては単なる**集合/写像**だが、それがモノイドという数学的構造の一部に組み込まれれば、「**モノイドの台集合**」や「**モノイドの二項演算**」という役割を担う。
レゴブロックにおいて、役割としての「**顔**」には、「ワニの**顔**」だけでなく「お馬さんの**顔**」もある。役割が「**顔**]でも、「ワニの**顔**]の実体は黄緑のブロックだし、「お馬さんの**顔**」は黄色いブロックになる。
数学においても、役割としての「**二項演算**」には、「モノイドの**二項演算**」だけでなく「ベクトル空間の**二項演算**(足し算)」もある。「モノイドの**二項演算**」と「ベクトル空間の**二項演算**」は同じ「二項演算」という呼び名(構造における役割名)だが、実体としては違うだろう。
==練習問題: 1== [2/ A07ans A07の問題の解答例 // 強行突破の背景](https://hackmd.io/@m-hiyama/SknLOJnZu#%E5%BC%B7%E8%A1%8C%E7%AA%81%E7%A0%B4%E3%81%AE%E8%83%8C%E6%99%AF) には、半環 $({\bf Z}_{-\infty}, \vee, -\infty, +, 0)$ が登場する。この半環における、「足し算」「ゼロ」や「掛け算」「イチ」が何であるか、もう一度考えてみよ。
自然言語ベースの用語(例:「モノイド」、「二項演算」、「単位元」)だけではなく、$A, f$ のようなラテン文字や $\cdot, \times$ のような記号や $\id$ のような名前がどんな用法で何を指しているのか、あるいは指してないのか? を、==正確に解釈し続ける==。オーバーロード/コンフリクトは日常茶飯事だから、同じ見た目の文字・記号・名前が出現位置ごとに違う意味を持つこともある。
## どうもやっぱり自然言語じゃダメみたい
と、言葉の使い方/解釈の仕方を繰り返し・繰り返し・繰り返し注意しているのだが、自然言語ではやはり ==“ボンヤリした印象・感情による解釈”からの脱却== が難しそうなので、新しい概念の導入〈introduction〉時の定義にも半形式的記述〈semi-formal description〉を用いることにする。
## モノイドの指標
我々の主題のひとつは指標〈signature〉だが、指標の典型的・代表的構文を使って、モノイドの指標を書いてみると:
```
signature Monoid {
sort U
operation m:U×U → U
operation e:1 → U
equation assoc:: m × id_U = α_(U, U, U) ; id_U × m ; m
equation lunit:: e × id_U ; m = λ_U
equation runit:: id_U × e ; m = ρ_U
}
```
プレーンテキストで書いているので、太字、下付き添字が使えないが、TeXを使えるなら:
| プレーンテキスト | TeX |
|----------------|------|
| 1 |${\bf 1}$ |
| id_U |$\id_U$ |
| α_(U, U, U) |$\alpha_{U, U, U}$ |
| λ_U |$\lambda_U$ |
| ρ_U |$\rho_U$ |
ギリシャ文字ラムダは、ラムダ記法ではなくて ${\bf 1}\times U \cong U$ という同型を与える同型写像〈可逆写像〉。==文字がコンフリクト==してるだけ。漢らしく、コンフリクトを気にしないで書くと:
$\For A \in |{\bf Set}|\\
\WeWillDefine \lambda_A:{\bf 1}\times A \to A \In {\bf Set}\\
\WeDefine \lambda_A := \lambda\, (*, a)\in {\bf 1}\times A.\, a$
2箇所に出現しているギリシャ文字ラムダの意味は==まったく違う==。ちなみに、$:=$ の左に出現しているラムダの写像〈巨大な写像〉としてのプロファイルは:
$\quad \lambda: |{\bf Set}| \to \mrm{Mor}({\bf Set})$
あるいは、
$\quad |{\bf Set}|\ni A \mapsto \lambda_A \in \mrm{Mor}({\bf Set})$
念の為、$\alpha$ と $\rho$ も定義しておくと:
$\For A, B, C \in |{\bf Set}|\\
\WeWillDefine \alpha_{A, B, C}: (A\times B)\times C \to A\times (B\times C) \In {\bf Set}\\
\WeDefine \alpha_{A, B, C} := \lambda\, ( (a, b), c )\in (A\times B)\times C.\, ( a, (b, c) )$
$\For A \in |{\bf Set}|\\
\WeWillDefine \rho_A: A\times {\bf 1} \to A\In {\bf Set}\\
\WeDefine \rho_A := \lambda\, (a, *)\in A\times {\bf 1}.\, a$
上記の指標は、集合圏で解釈することを==暗黙の前提==にしているが、暗黙がイヤなら明示的に書く。
```
signature Monoid {
sort U in Set
operation m:U×U → U in Set
operation e:1 → U in Set
equation assoc:: m × id_U = α_(U, U, U) ; id_U × m ; m in Set
equation lunit:: e × id_U ; m = λ_U in Set
equation runit:: id_U × e ; m = ρ_U in Set
}
```
行末の「in Set」を繰り返し何度も書くのがイヤなら:
```
signature Monoid within Set {
sort U
operation m:U×U → U
operation e:1 → U
equation assoc:: m × id_U = α_(U, U, U) ; id_U × m ; m
equation lunit:: e × id_U ; m = λ_U
equation runit:: id_U × e ; m = ρ_U
}
```
1行目の「within Set」ですべて集合圏内で解釈することを明示する。
集合圏で解釈するのだから、
- sort は集合圏の対象、つまり集合を意味する。
- operation は集合圏の射、つまり写像〈関数〉を意味する。
- equation は射〈写像〉のあいだの等式を意味する。
伝統的キーワード sort, operation, equation の代わりに味気ないキーワードを使ってもよい(キーワード選択は趣味の問題)。
```
signature Monoid within Set {
0-mor U
1-mor m:U×U → U
1-mor e:1 → U
2-mor assoc:: m × id_U ⇒ α_(U, U, U) ; id_U × m ; m :(U×U)×U → U
2-mor lunit:: e × id_U ; m ⇒ λ_U :1×U → U
2-mor runit:: id_U × e ; m ⇒ ρ_U :U×1 → U
}
```
- 0-mor は集合圏の0-射、つまり対象を意味する。
- 1-mor は集合圏の1-射、つまり射を意味する。
- 2-mor は集合圏の2-射、つまり1-射のあいだの等式を意味する。
等式を、2-射のプロファイルの記法で書いた。同じ等式を集合圏内の可換図式で書けば以下のとおり。可換図式内の多角形は、2-射としての“膜”が張っているとみなす。
$\require{AMScd}
\begin{CD}
(U\times U)\times U @>{\alpha_{U, U, U}}>> U\times (U\times U)\\
@V{m\times \id_U}VV @VV{\id_U \times m}V\\
U\times U @. U\times U\\
@V{m}VV @VV{m}V\\
U @= U
\end{CD}\\
\text{commutative in }{\bf Set}$
$\begin{CD}
{\bf 1}\times U @>{e \times \id_U}>> U\times U\\
@V{\lambda_U}VV @VV{m}V\\
U @= U
\end{CD}\\
\text{commutative in }{\bf Set}$
$\begin{CD}
U\times {\bf 1} @>{ \id_U\times e}>> U\times U\\
@V{\rho_U}VV @VV{m}V\\
U @= U
\end{CD}\\
\text{commutative in }{\bf Set}$
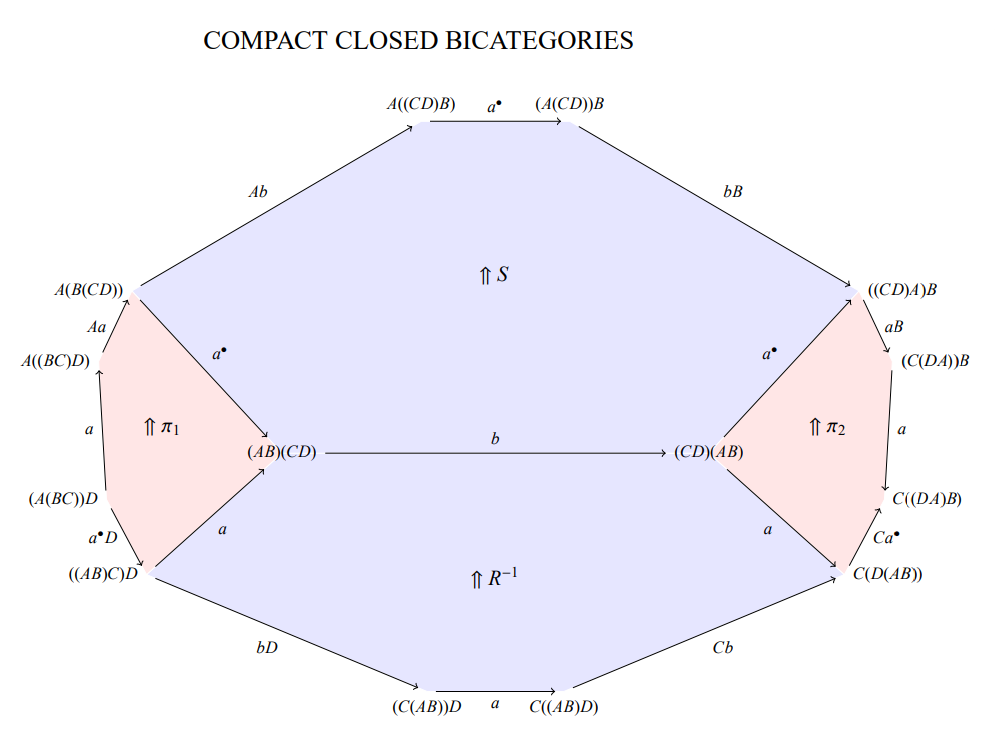
マイク・ステイの絵のように、2-射の“膜”を色付きで示せばわかりやすい。ほとんどの人はそこまで出来ないが(色付き絵は面倒過ぎる)。
## 法則の書き方
モノイドの指標のなかで、assoc, lunit, runit はモノイドの法則になる。法則は射のあいだの等式(または可換図式)で書くのが圏論との相性がいいが、述語〈predicate〉を使ったり、論理式を使ったりしてもよい。
述語〈predicate〉を定義して法則を記述する例:
```
signature Monoid within Set {
sort U
operation m:U×U → U
operation e:1 → U
defPred assocPred := λ(a, b, c)∈U×U×U. eq_U( m(m(a, b), c), m(a, m(b, c)) )
defPred lunitPred := λa∈U. eq_U( m(e(*), a), a )
defPred runitPred := λa∈U. eq_U( m(a e(*)), a )
equation assoc :: assocPred = True_(U×U×U)
equation lunit :: lunitPred = True_U
equation runit :: lunitPred = True_U
}
```
defPredは述語(ブーリアン真偽値集合 = ${\bf B}$ に値を持つ関数)を定義している。プレーンテキストじゃなくてTeXで書くなら:
$\For U\in |{\bf Set}|\\
\WeWillDefine \mrm{assocPred}: U\times U\times U \to {\bf B} \In {\bf Set}\\
\WeDefine \mrm{assocPred} :=
\lambda\, (a, b, c)\in U\times U\times U.\,
\mrm{eq}_U( m(m(a, b), c), m(a, m(b, c)) )$
$\mrm{eq}_U$ は集合 $U$ 上で定義された等値述語(イコール述語)。
$\quad \mrm{eq}_U : U\times U \to {\bf B}\In {\bf Set}$
さて、集合U上の述語を定義したことと、その述語が真であることは==まったく別==である。
- [フェイク情報に騙されないために](https://hackmd.io/@m-hiyama/ryND05Bgu#%E3%83%95%E3%82%A7%E3%82%A4%E3%82%AF%E6%83%85%E5%A0%B1%E3%81%AB%E9%A8%99%E3%81%95%E3%82%8C%E3%81%AA%E3%81%84%E3%81%9F%E3%82%81%E3%81%AB) 参照。命題を目にすることと、その命題が真であることはまったく別! 数学だけではなく日常生活でもとても大事なこと。
モノイドの法則は、定義した述語 assocPred, lunitPred, runiPred が真であることを要求するので、これらの述語(ブーリアン真偽値集合に値を持つ関数)が、“常に真である述語”と述語として(関数として)等しいことを要求する。そのファクトチェック要求が:
```
equation assoc :: assocPred = True_(U×U×U)
equation lunit :: lunitPred = True_U
equation runit :: lunitPred = True_U
```
ここで、
$\For X\in |{\bf Set}|\\
\WeWillDefine \mrm{True}_X: X \to {\bf B} \In {\bf Set}\\
\WeDefine \mrm{True}_X :=
\lambda\, x\in X.\, 1$
assocPred = True_(U×U×U) は次のこと:
$\quad
\lambda\, (a, b, c)\in U\times U\times U.\,
\mrm{eq}_U( m(m(a, b), c), m(a, m(b, c)) ) = \lambda\, (a, b, c)\in U\times U\times U.\, 1$
関数が等しいことは、すべての関数値が等しいことだから、
$\quad
\forall (a, b, c)\in U\times U\times U.\,
\mrm{eq}_U( m(m(a, b), c), m(a, m(b, c)) ) = 1$
$\mrm{eq}_U(x, y ) = 1$ は $x = y$ と書いてもよいから:
$\quad
\forall (a, b, c)\in U\times U\times U.\,
m(m(a, b), c) = m(a, m(b, c))$
これで結合法則の論理式が得られた。
数学では常に:
- **ちゃんと書くとメンドクセー、鬱陶しい、だるい。省略しちゃえ、暗黙の前提にしちゃえ、文脈からわかるだろう。文脈読めねー奴なんて知らねーわ。**
という誘惑&圧力が働き、==実際に省略・暗黙化・文脈化が行われる==。実用上は、省略・暗黙化・文脈化しても困らない(むしろ便利になる)が、論理的関係を追うのは困難になる。自分で、省略されて見えなくなった繋がりを補う必要がある。
まーともかく、法則を論理式で書いた次の書き方も許す。
```
signature Monoid within Set {
sort U
operation m:U×U → U
operation e:1 → U
law assoc : ∀(a, b, c)∈U×U×U. m(m(a, b), c) = m(a, m(b, c))
law lunit : ∀a∈U. m(e(*), a) = a
law runit : ∀a∈U. m(a e(*)) = a
}
```
この書き方は見慣れているから読みやすいかも知れない。が、law の解釈が素直に射にならない(ひねくれた射になる)ので、圏論的には扱いにくくて嬉しくない。圏論的に扱いやすいのは、2-射としての等式による記述である。
==語学的注意:== 述語定義や論理式を書いたら、それはもはや指標〈signature〉ではない。仕様〈specification〉と呼ぶべきだという意見もある。が、==ここでは、== その区別を厳密にしても特にメリットがないので、指標と仕様の区別はしない。指標と仕様を区別したほうが良い場面も当然にあるだろう。
<b>[追記]</b>この節に対する追加サンプルあり → [B02A 追加サンプル](https://hackmd.io/@m-hiyama/Skpb0mo3t)<b>[/追記]</b>
## モノイドの半形式的記述
指標を使った書き方と内容的には同じだが、より可読性を上げた構文を導入する。
$\WeIntroduce M = (U, m, e) \As \text{monoid}\\
\Where\\
\quad U \in |{\bf Set}| \As \text{underlying set}\\
\quad m : U\times U \to U \In {\bf Set} \As
\text{multiplication}\\
\quad e:{\bf 1} \to U \In {\bf Set} \As
\text{unit}\\
\Requires\\
\quad \forall x, y, z \in U. \\
\qquad m(m(x, y), z) = m(x, m(y, z))
\As \text{associative law}\\
\quad \forall x \in U. \\
\qquad m(e(*), x) = x
\As \text{left unit law}\\
\quad \forall x \in U. \\
\qquad m(x, e(*) ) = x
\As \text{right unit law}$
前節の、論理式で法則を書いた指標に比べて、変更点と改善点は:
1. プレーンテキストではなくてTeXで書く。
1. 構文のフレーバーが今までの半形式的記述と同じ。
2. 色付きキーワードにより見やすくなっている。
3. $\Keyword{As}$ により、構造や構成素の呼び名を指定できる。
上記の導入定義〈Introduction〉は、抽象的・公理的にモノイドを定義しているもので、モノイドの具体例ではない。具体例記述〈インスタンスの定義〉は次のようにする。
モノイドの具体例として、自然数の掛け算のモノイドを定義する。
$\WeInstantiate \text{monoid } M \assig \mathsf{NatMulMon} \\
\Where\\
\quad U \assig {\bf N} \in |{\bf Set}|\\
\quad m \assig (\times):{\bf N}\times{\bf N} \to {\bf N} \In {\bf Set}\\
\quad e \assig 1^\sim : {\bf 1} \to {\bf N} \In {\bf Set}\\
\Justification\\
\quad \forall x, y, z \in {\bf N}. \\
\qquad (\times)( (\times)(x, y), z) = (\times)( x, (\times)(y, z)) \\
\quad \forall x \in {\bf N}. \\
\qquad (\times)(1^\sim(*), x) = x\\
\quad \forall x \in {\bf N}. \\
\qquad (\times)(x, 1^\sim(*) ) = x$
表で示すと:
| 一般論(抽象的) | 特定具体例 |
|--------|------------|
|$M$ | $\mathsf{NatMulMon}$ |
|$U$ | ${\bf N}$ |
|$m$ | $(\times)$ |
|$e$ | $1^\sim$ |
|一般的法則 | 具体的法則 |
“抽象的一般概念モノイド”の特定具体例である $\mathsf{NatMulMon}$ は、$\text{monoid }({\bf N}, (\times), 1^\sim)$ のように書くことができる。
==注意:== なるべく、固有名はボールド体 ${\bf Name}$ 、サンセリフ $\mathsf{Name}$ 、黒板文字 $\mathbb{NAME}$ で書くようにするが、完全に守れる自信はない。固有名かそうでないかはフォントに頼らず毎度確認したほうがよい。
## Of, IsA, ClassOf
キーワード $\As$ で導入された構成素の役割名〈role name \| field name〉とキーワード $\Of$ を組み合わせると、数学的構造物(今はモノイド)の特定の構成素を取り出せるとする。
- $\text{underlying set} \Of \mathsf{NatMulMon}$ : モノイド(の具体例) $\mathsf{NatMulMon}$ の台集合〈underlying set〉
- $\text{unit}\Of \mathsf{NatMulMon}$ : モノイド(の具体例) $\mathsf{NatMulMon}$ の単位元〈unit〉(のポインティング写像)
キーワード $\IsA$ を使って、
$\quad
\mrm{IsMonoid}(X) \Iff X \IsA \text{monoid}$
により、数学的存在物 $X$ がモノイドであることを示す。$\mrm{IsMonoid}$ は集合論の命題としてハッキリと定義できるが、今は触れない。直感的に「$X$ はモノイドである」という命題を $X \IsA \text{monoid}$ と書けると了解すればよい。
すべての数学的存在物が含まれる集合論の宇宙を ${\bf Univ}$ として、次の集合を考える。
$\quad
\{ X \in {\bf Univ} \mid X \IsA \text{monoid}\}$
これは、集合論で認められる集合ではなくて類〈class〉である。この類を次の書き方で表す。
$\quad
\ClassOf \text{monoid}\Things$
モノイドの圏を ${\bf Mon}$ としたとき、
$\quad |{\bf Mon}| =
\ClassOf \text{monoid}\Things$
が成立する。
$\ClassOf \cdots \Things$ は、「$\cdots$ と呼ばれるすべての数学的モノ達からなる類」の意味で、圏を作る前に対象の類だけ先に定義する際に便利。キーワードに"class"という曖昧多義語([D01 混乱しがちな言葉](https://hackmd.io/@m-hiyama/S19pMmljK) 参照)を入れると、変な連想や誤解を誘発するリスクはあるが。
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet