---
tags: TrRun4
id: Theo-E10_realworld-math.md
---

# 檜山トレラン4 E10 これが現実‥‥

$\newcommand{\mrm}[1]{\mathrm{#1} }
\newcommand{\id}{\mathrm{id}}$

2020-02-18のLINEグループ投稿：

> 

## 解消できないストレスの解消法

不満は募るが==状況改善はあり得ない==とき：

1. 愚痴を言って慰め合う。→ いつもやっている。
2. より良い世界を妄想する。→ [3/ A05 閃きと飛躍、記法の獄舎、異世界転生 // 異世界転生学習法](https://hackmd.io/@m-hiyama/HyefK6w1t#%E7%95%B0%E4%B8%96%E7%95%8C%E8%BB%A2%E7%94%9F%E5%AD%A6%E7%BF%92%E6%B3%95)
3. 理由に納得して多少の精神安定を得る。

### プライベート／ローカルに異世界を作る

[3/ A05 閃きと飛躍、記法の獄舎、異世界転生](https://hackmd.io/@m-hiyama/HyefK6w1t) 内で参照した <https://twitter.com/esumii/status/1376713802025115648> ：


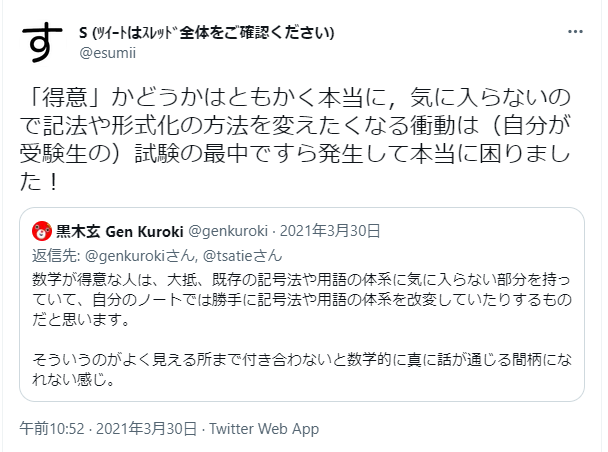
世間が変わらないなら、自分／自分達だけのより良い用語法・記法・定式化で記述や計算をするってこと。これはこれでセクショナリズムを助長するが。

### なんでこんなことに？

1. セクショナリズム → [D01 混乱しがちな言葉](https://hackmd.io/@m-hiyama/S19pMmljK)
2. 速記原則〈[モノグサ原則](https://hackmd.io/@m-hiyama/rJPvLaOJc)〉
3. エリートバイアス（一種の[生存者バイアス](https://ja.wikipedia.org/wiki/%E7%94%9F%E5%AD%98%E8%80%85%E3%83%90%E3%82%A4%E3%82%A2%E3%82%B9)）

## 「これが現実‥‥」体験

指標とセオリーがどのように定義されているか、現実の様々な定義を見てみよう。漫然と読むと混乱するだけだが、注意深く読めば、用語法や定義の相互関係が分かり==多面的な見方からより深い理解==が得られる。我々の〈ローカルな〉標準的用語・定義と比較してみよう。

### ザンサイ／リャン

- Title: Rewriting in Free Hypergraph Categories
- Author: Fabio Zanasi
- Submitted: 27 Dec 2017 (v1), 3 Jan 2018 (v2)
- URL: <https://arxiv.org/abs/1712.09495>

> 

- Title: Free CD Categories
- Author: Wendong Liang
- Submitted: August 19, 2021
- URL: <https://www.uibk.ac.at/mathematik/algebra/teaching/m1these_wendong_liang.pdf>

リャンはザンサイをほとんどそのまま引用しているが、微妙な変更はしている。

> 

雑訳：

> モノイドセオリーとは、全順序指標 $\Sigma$ と、色の全順序有限集合 $C$ の組 $(\Sigma , C)$ のこと。$\Sigma$ の要素は、アリティ $w$ 、コアリティ $v$ のオペレーション $o:w \to v$ 、ここで $w, v\in C^*$ 。

重要語／記号：

1. monoidal theory〈モノイドセオリー〉
2. signature〈指標〉
3. color〈色〉
4. operation〈オペレーション〉
5. arity, coarity〈アリティ、コアリティ〉
6. $C^*$

### ゴグエン／バーストル

ゴグエン／バーストルの定義を（教育の観点から）==そのままは使えないな==、と思っているのだけど、オリジナルの定義を見てみよう。

- Title: Institutions: Abstract Model Theory for Specification and Programming
- Authors: JOSEPH A. GOGUEN, ROD M. BURSTALL
- Year: 1992
- URL: <https://courses.engr.illinois.edu/cs522/sp2016/InstitutionsAbstractModelTheory.pdf>

#### インスティチューションの定義

> 

雑訳：

> インスティチューション $\mathscr{I}$ は次の構成素からなる。
> 1. 圏 ${\bf Sing}$ 、その対象は指標と呼ばれる、
> 2. 関手 $Sen:{\bf Sing} \to {\bf Set}$ 、各指標に対して集合を割り当てる、その集合の要素はその指標上の文と呼ばれる、
> ...[以下略]...

重要語／記号：

1. signature〈指標〉
2. sentence〈文〉

#### セオリーやプレゼンテーションの定義

プレゼンテーションは、別文書では「仕様〈specification〉」と呼んでいる。

> 

雑訳：

> $\mathscr{I}$ は、任意に選ばれて固定されたインスティチューションとする。そのとき、
> 1. $\Sigma$-プレゼンテーションとはペア $\langle \Sigma, E\rangle$ 、ここで、$\Sigma$ は指標で、$E$ は$\Sigma$-文の集まり、
> 2. ...[省略]...
> 3. ...[省略]...
> 4. $\Sigma$-モデルの集合 $M$ が与えられたとして、$M^*$ は $M$ の各モデルにより充足されるすべての$\Sigma$-文の集まりとする。$M^*$ は $\langle \Sigma, M^*\rangle$ とも書き、$M$ のセオリーと呼ぶ。
> 5. ...[以下略]...

重要語／記号：

1. $\Sigma$-presentation〈$\Sigma$-プレゼンテーション〉
2. theory of $M$〈$M$ のセオリー〉

#### （教育の観点から）使えない理由

1. 抽象的過ぎる。
2. 構造が複雑大規模過ぎる。
3. 仕様〈プレゼンテーション〉の論理的側面を重視しているので、論理の話題が多い（多過ぎる）。
4. 論理的真偽が、証明ではなくて超越的な充足性〈satisfaction〉により決まる。人によっては分かりにくいだろう。
5. 指標から型や関数を定義する部分が入ってない。（そこは別に論じる前提）
6. 1-指標に限定している。0-指標／2-指標を想定してない（たぶん）。
7. 指標〈プレゼンテーション \| 仕様〉の無法則部〈lawless part〉と法則〈文〉の区切りが固定されているのは使いにくい。

### ステイ／メリデス

- Submitted: 7 Oct 2016 (v1), 16 Oct 2016 (v3)
- Title: Logic as a distributive law
- Authors: Mike Stay, Lucius Gregory Meredith
- URL: <https://arxiv.org/abs/1610.02247>

ステイ／メリデスは、単ソート指標／単ソートセオリーしか扱ってない。比較的、ローヴェアに忠実。

> 

雑訳：

> $\mrm{FinSet}$ は有限集合の圏の骨格とする。計算的計算〈computational calculus〉のローヴェアセオリーとは、有限積を持つ圏 $\mrm{Th}(\mrm{Calc})$ で、対象上で恒等な反変関手 $\theta:\mrm{FinSet}^\mrm{op} \to \mrm{Th}(\mrm{Calc})$ を備えたものである。$\mrm{FinSet}$ の対象は単元集合の余積だから、$\mrm{Th}(\mrm{Calc})$ の対象も生成対象の直積となる。生成対象は、"sort" にちなんで$S$ と書く。$\mrm{Th}(\mrm{Calc})$ の射は、$S$ の有限ベキから $S$ への射達の集合から、積と結合で生成される。よって、圏 $\mrm{Th}(\mrm{Calc})$ は次のもの達で表現〈present〉されるだろう。
...[以下略]...

重要語／記号：

1. $\mrm{FinSet}$
1. Lawvere theory〈{ローヴェア}?セオリー〉
2. generating object〈生成対象〉
3. sort〈ソート〉
4. term constructor〈項構成子〉
5. equation〈等式〉
6. arity〈アリティ〉
7. present〈表現〉

$\mrm{FinSet}$ の参考：


### スピヴァック／ケント

- Title: Ologs: a categorical framework for knowledge representation
- Authors: David I. Spivak, Robert E. Kent
- Submitted: 9 Feb 2011 (v1), 7 Aug 2011 (v2)
- URL: <https://arxiv.org/abs/1102.1889>

節の冒頭で何気なく言葉の定義を済ませている。

> 

雑訳：

イタリック体を太字にする。

> この節では、今まで述べたことをすべてクリアかつ厳密にする。既に述べたように、我々は圏そのものではなくて、圏のプレゼンテーション（ここではそれを**仕様**と呼ぶ）を扱う。我々は、ファイバーと呼ばれる一様なコンテキストを詳しく議論して、充足性の公理を与える。そして、グラフ（ologのあいだの辞書の変換）のあいだの射が、一様なファイバー・コンテキストのあいだの順方向／逆方向の情報フローをどのように記述するかを議論する。最後に、仕様（**セオリー**ともいう）とオントロジーのためのセオリーの束〈そく〉について議論する。

重要語／記号：

1. presentation〈プレゼンテーション〉
2. specification〈仕様〉
3. theory〈セオリー〉

スピヴァック／ケントが、バーワイズやゴグエン／バーストルを知らないわけではない。

> 

雑訳：

> ...[snip]... 情報フロー理論の開発を先導したことに関してジョン・バーワイズに感謝する。インスティチューション理論の開発を先導したこと、そして、情報フロー理論とインスティチューション理論を使った知識表現に対する共通アプローチを指し示したことに関してジョセフ・ゴグエンに感謝する。

### 追記： ボンチ他

- Submitted: 3 Dec 2020 (v1), 3 Feb 2022 (v2)
- Title: String Diagram Rewrite Theory I: Rewriting with Frobenius Structure
- Authors: Filippo Bonchi, Fabio Gadducci, Aleks Kissinger, Pawel Sobocinski, Fabio Zanasi
- Pages: 57p
- URL: <https://arxiv.org/abs/2012.01847>

> 

雑訳：

> モノイド指標とは、 決まったアリティ $n$ と コアリティ $m$（$n, m\in \mathbb{N}$）に対するオペレーション $f:n \to m$ からなる集合 $\Sigma$ である。対称モノイド・セオリーは、$\Sigma$-項を使って定義される。$\Sigma$-項の集合は、$\Sigma$ のオペレーション／恒等 $\id_n:n \to n$ ／対称 $\sigma_{n, m}:n + n \to m + n$（$n, m\in \mathbb{N}$）を、順次（$;$）と並列（$\otimes$）の結合により組み合わせることにより得られる。これは純粋に形式的なプロセスで： 与えられた $\Sigma$-項 $r:m \to n, s:n \to o, t:m' \to n'$ に対して、我々は新しい項 $r;s : m \to o,\, r\otimes t:m + m' \to n + n'$ を構成できる。
>
> 定義 2.1. **対称モノイド・セオリー**とは、ペア $(\Sigma, \mathscr{E})$ で、$\Sigma$ はモノイド指標、$\mathscr{E}$ は等式の集合である。等式とは、同じアリティ・コアリティを持つ$\Sigma$-項 $l, r:v \to w$ のペア $\langle l, r\rangle$ である。

重要語／記号：

1. monoidal signature〈モノイド指標〉
3. symmetric monoidal theory〈対称モノイド・セオリー〉
2. arity, coarity〈アリティ、コアリティ〉
4. $\Sigma$-term〈$\Sigma$-項〉
5. identity〈恒等〉
6. symmetry〈対称〉
7. purely formal process〈純粋に形式的なプロセス〉
8. equation〈等式〉

==注意：== 小学校の分数／中学校の多項式以来、同値関係で割る前と割った後（分数表記と有理数）の区別が曖昧だが、その曖昧さはずっと解消されない。ここでの $\Sigma$-項の意味も実は曖昧。これも==広く浸透した悪習==。

### 追記：clone （nLab項目）

- <https://ncatlab.org/nlab/show/clone>

これはテキストでコピー。

> **2. Definition**
>
> A set of algebraic operations on a fixed set $S$ is a **(concrete) clone** on $S$ if it contains all (component) projections $S^n \to S$ and is closed under composition (“superposition”).
>
> An **abstract clone** consists of an abstract set of “$n$-ary operations” for every $n$ together with projection and composition operations. For now, see [wikipedia](https://en.wikipedia.org/wiki/Clone_%28algebra%29). This is the notion that’s equivalent to a cartesian operad or a Lawvere theory.

雑訳：

> **2. 定義**
>
> 決まった集合 $S$ 上の代数的オペレーションの集合は、次の条件を満たすとき **(具象)クローン**と呼ばれる； 条件： その集合は、すべての(成分)射影 $S^n \to S$ を含み、結合(“重ね合わせ”)に関して閉じている。
>
> **抽象クローン**は、すべての $n$ に対する“$n$-項オペレーション”の抽象的集合と射影達、それと結合演算から構成される。あとは WikiPedia 見てね。これは、デカルト・オペラッドやローヴェア・セオリーと同値な概念である。

重要語／記号：

1. concrete clone〈具象クローン〉
2. abstract clone〈抽象クローン〉
3. $n$-ary operation〈$n$-項オペレーション〉
4. composition operation〈結合演算〉
5. cartesian operad〈デカルト・オペラッド〉
6. Lawvere theory〈ローヴェア・セオリー〉

### 追記： フォング

過去に出したことがある。[3 B01 参考文献](https://hackmd.io/@m-hiyama/BJLL21Z0u) 参照。

- Name: Fong
- Title: Causal Theories: A Categorical Perspective on Bayesian Networks
- Author: Brendan Fong
- Date: 26 Jan 2013
- Pages: 77p
- URL: <https://arxiv.org/abs/1301.6201>, <https://arxiv.org/pdf/1301.6201.pdf>

> 

雑訳：

> ...[snip]...
> 我々は、この圏 $\mathcal{C}_G$ を因果構造 $G$ の**因果セオリー**と呼ぶ。$\mathcal{C}_G$ の射は、与えられた域変数に関する知識から余域変数の出力を予測する方法を表す。

重要語／記号：

1. causal theory〈因果セオリー〉
2. causal structure〈因果構造〉

### 追記： パターソン

- Name: Patterson
- Title: The algebra and machine representation of statistical models
- Author: Evan Patterson
- Date: 16 Jun 2020
- Pages: 224p
- URL: <https://arxiv.org/abs/2006.08945>, <https://arxiv.org/pdf/2006.08945.pdf>

> 

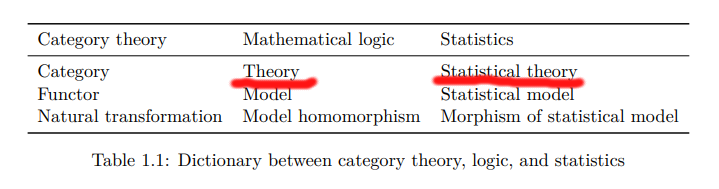
パターソンは檜山と同じ用語法を使っている。ただし、考える指標を固定（決め打ち）しているので、「指標」は使ってない。この表を理解するのが、本セミナーの目標のひとつ。圏の文法から作られるセオリーをマルコフ圏で解釈する場合に、この表の対応がバッチリ成立する。

フォングもパターソンも、暗黙に圏の文法（より正確にはマルコフ圏の文法）を想定して、圏をセオリーと呼んでいる。想定している文法は==暗黙になりがち==だから注意。0-指標や2-指標だと、大枠は同じでも個別の事情は変わる。

<hr>

ベイズ確率統計のためのセオリー論については以前から言及している。

- [3/ A23 圏論的コンビネーションとグラフィカルモデル // 語学的注意： セオリーの理論](https://hackmd.io/@m-hiyama/ryIN0OrXY#%E8%AA%9E%E5%AD%A6%E7%9A%84%E6%B3%A8%E6%84%8F%EF%BC%9A-%E3%82%BB%E3%82%AA%E3%83%AA%E3%83%BC%E3%81%AE%E7%90%86%E8%AB%96)
- [3/ A25 一般コンビネーション(次ネタ?) // コンビネーションの奥義](https://hackmd.io/@m-hiyama/ByWhppIXF#%E3%82%B3%E3%83%B3%E3%83%93%E3%83%8D%E3%83%BC%E3%82%B7%E3%83%A7%E3%83%B3%E3%81%AE%E5%A5%A5%E7%BE%A9)
- [ブログ記事： ローヴェア流セオリー論と統計モデル](https://m-hiyama.hatenablog.com/entry/2021/02/17/132949)

<!--
## ロドリゲス達

- Submitted: on 21 Jun 2011
- Title: Refinement by interpretation in π-institutions
- Authors: César Rodrigues, Manuel A. Martins, Alexandre Madeira, Luis S. Barbosa
- URL: <https://arxiv.org/abs/1106.4093>

-->