# 探索式多變量 HW1
###### tags: `multivariate`

## URL
https://hackmd.io/q20Hza-cQZCGyfHSiWxgnw

## 1
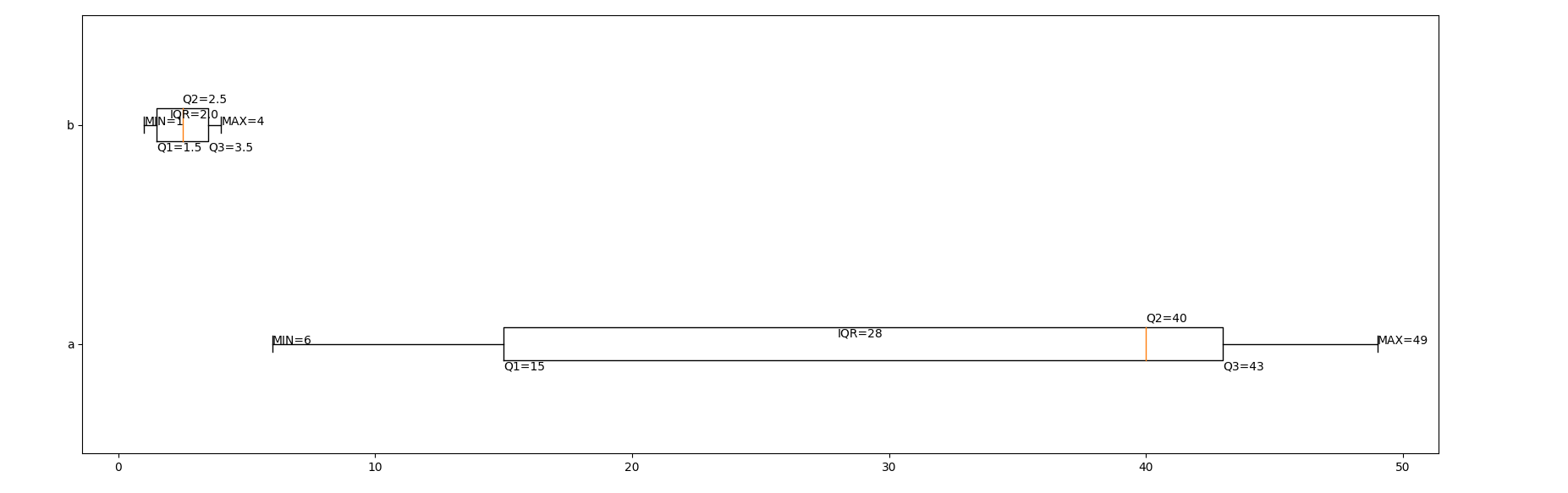
請畫出下列兩組數據組的盒鬚圖(5分)
需標示清楚(內籬[即為`Q1 - 1.5*IQR`, `Q3 + 1.5*IQR`], Q1 ,Q2, Q3, Max, min)
> 我這裡是用 https://zh.wikipedia.org/wiki/%E5%9B%9B%E5%88%86%E4%BD%8D%E6%95%B0#%E8%BF%90%E7%AE%97%E8%BF%87%E7%A8%8B 來計算四分位
* a: 6,47,49,15,42,41,7,39,43,40,36
* b: 4,3,1,2
> 
> Please see python code https://gist.github.com/linnil1/e61426e345675712ea18038d824b6b73

## 2 請計算下列分配的期望值與變異數,但其一表格被咖啡汙染(5分)
| x | 0 | 1 | 2 | 3 |
|:---:| --- | --- | --- | --- |
| f(x) <br> probability mass function| 0.2 | 0.45| 0.3 | 咖啡漬 |

> $咖啡漬 = 1 - 0.2 - 0.45 - 0.3 = 0.05$
> $E(X) = 0 * 0.2 + 1 * .45 + 2 * .3 + 3 * .3 = 1.95$
> $Var(X)= E(X^2) - (E(X))^2 = 0^2 * 0.2 + 1^2 * .45 + 2^2 * .3 + 3^2 * .3 - 1.95^2 = 0.5475$

## 3 請計算一次投擲4顆骰子,出現2個5點的機率為何? (5分)
> 其實就是分成 出現 5 跟 沒出現 5。
> 出現5機率 $p=1/6$

此試驗服從 **Binomial** 分配且其參數為 **就是骰子數 $n = 4$**
如題機率為?
> $$
> C^{4}_{2}(1/6)^2(1 - 1/6)^2 = 0.116
> $$

## 重複投三次,兩次結果為出現2個5點的機率為何?
此時 三次 $n=3$ 然後出現 兩個五點 $p=0.116$ ，一樣是 binomial distribution
> $$
> C^{3}_{2}(0.116)^2(1 - 0.116)^1 = 0.036
> $$

## 4 Poisson 題
X是服從Poisson分配，每15分鐘平均有2人進入超商，每30分鐘平均有4人進入超商 ，所以 𝜆＝___，而9:00~9:30間，有5位顧客進入超商之機率為?(5分)
> 所求區間為 30min，所以 $\lambda=4$，而 $x = 5$，帶入 poisson distribution
> $$
> P = \frac{e^{-4}(4)^5}{5!} = 0.156
> $$

## 5 是非題
所謂的 $\bar{x}$ 抽樣分配,就是抽樣出來之樣本的平均所呈現的分布(5分)
> Yes, 而且這個分布根據中央極限定理，是常態分布。

## 6 填空
假設檢定列式,等號一定要放在 **Null hypothesis(虛無假設)** ,且錯誤決策會有重大損失的會放在 **Alternative Hypothesis(對立假設)**
(5分)

## 7 知名統計學家費雪曾說過一段經典故事,有位女士宣稱她可以分辨一杯奶茶是先加牛奶在加茶還是先加茶在加牛奶.如今日我們用假設檢定來做檢驗,
虛無假說=該女士實際無法分辨
在信心水準0.05下,端出5杯奶茶給女士品嘗且5杯全數答對,
其p值為__________,故我們__(拒絕/不拒絕)____虛無假設
(5分)
> 先假設亂猜，也就是 $p = 0.5$，所以全部答對 $P = 0.5 ^ 5 = 0.03125 < 0.05$，所以我們 reject null hypothesis

## 8 一組回歸數據
其 $\sum_{i=1}^{n} (\hat{y_i}-\bar{y})^2=800$, $\sum_{i=1}^{n} (\hat{y_i}-y_i)^2=200$ 請問其判別係數為何? (5分)
> 原來在問 coefficient of determination($R^2$)
> Total loss = 800 + 200
> error loss = 200
> $R^2 = 可解釋 / 全部 = (Total - error) / Total = 0.8$

## 9 Assume that IQ scores for a certain population are approximately N(µ,100).
To test H0: $µ=110$ against the one-sided alternative hypothesis H1: $µ>110$, we take a random sample of size n = 16 from this population and observe $\bar{x}=113.5$.
(a) Do we accept or reject H0 at the 5% significance level? (10 points)
> $H_0: \mu <= 110$
> $\sigma = \sqrt{100} = 10$
> 因為樣本數少於30所以使用 t-distribution 而非 normal-distribution
> $\frac{\bar{x} - \mu}{\sigma \ \sqrt{n}} = 1.4$
> `pt(1.4, 16)`
> 0.9096975 < 0.95
> 所以我們 fail to reject H0

## Bonus　(是非題) 因子分析與主成分皆為降維的工具,且使用目的也相同(3分)
> 是，都是降維工具
> 目的不一樣，我們可以從計算方式來看
> * PCA 是盡量把重要的東西取出來，但是都是orthogonal
> * FA 則可以刻意 oblique，畢竟每個成分可能是有關連的
>
> 解答
> 錯。因子分析在於找出影響各變項的背後之幾個共同因子，
主成分則是找出相近的變項並合併。