---
tags: crypto, ECDH, ECDSA
---

<style>

html, body, .ui-content {
background-color: #333;
color: #ddd;
}

.markdown-body h1,
.markdown-body h2,
.markdown-body h3,
.markdown-body h4,
.markdown-body h5,
.markdown-body h6 {
color: #ddd;
}

.markdown-body h1,
.markdown-body h2 {
border-bottom-color: #ffffff69;
}

.markdown-body h1 .octicon-link,
.markdown-body h2 .octicon-link,
.markdown-body h3 .octicon-link,
.markdown-body h4 .octicon-link,
.markdown-body h5 .octicon-link,
.markdown-body h6 .octicon-link {
color: #fff;
}

.markdown-body img {
background-color: transparent;
}

.ui-toc-dropdown .nav>.active:focus>a, .ui-toc-dropdown .nav>.active:hover>a, .ui-toc-dropdown .nav>.active>a {
color: white;
border-left: 2px solid white;
}

.expand-toggle:hover,
.expand-toggle:focus,
.back-to-top:hover,
.back-to-top:focus,
.go-to-bottom:hover,
.go-to-bottom:focus {
color: white;
}

.ui-toc-dropdown {
background-color: #333;
}

.ui-toc-label.btn {
background-color: #191919;
color: white;
}

.ui-toc-dropdown .nav>li>a:focus,
.ui-toc-dropdown .nav>li>a:hover {
color: white;
border-left: 1px solid white;
}

.markdown-body blockquote {
color: #bcbcbc;
}

.markdown-body table tr {
background-color: #5f5f5f;
}

.markdown-body table tr:nth-child(2n) {
background-color: #4f4f4f;
}

.markdown-body code,
.markdown-body tt {
color: #eee;
background-color: rgba(230, 230, 230, 0.36);
}

a,
.open-files-container li.selected a {
color: #5EB7E0;
}

</style>

# Elliptic Curve Cryptography

Today, *Elliptic Curve Cryptography* (**ECC**) appears in [TSL](https://tools.ietf.org/html/rfc4492), [SSL](https://tools.ietf.org/html/rfc5656), [PGP](https://tools.ietf.org/html/rfc6637), and many other things including [Bitcoin](https://en.bitcoin.it/wiki/Elliptic_Curve_Digital_Signature_Algorithm) and [Blockchain](https://arxiv.org/ftp/arxiv/papers/1808/1808.02988.pdf).

## **The Goal**

(My application is based on C language, but in the blog I will explain ECC in Python language to skip bignum part.)

I explain how I applied ECC algorithm on secure transmission channel from server to client. I used *Elliptic Curve Diffie-Hellman* (**ECDH**) key exchange to generate keys for *Advanced Encryption Standard* (**AES**). That key used to encrypt the data exchanged between the client and the server.

In addition, I use of *Elliptic Curve Digital Signature Algorithm* (**ECDSA**) as a authentication mechanism.

### **ECC Over Finite Fields GF\(p\)**

In mathematics, elliptic curve is described in [here](https://mathworld.wolfram.com/EllipticCurve.html). But in cryptography, an elliptic curve have the form known as:

$$
y^2 = x^3 + ax + b\, (\,mod \,\, p)
$$

satisfied

$$
\\4a^3 + 27b^2 \ne 0.
$$

This is required to exclude [singular curves](https://en.wikipedia.org/wiki/Singularity_(mathematics)).

Example: [link](https://www.desmos.com/calculator)

$$
\\ y^2 = x^3 - x + 4
$$


### **Group operator on ECC**

For an elliptic curve, I have a set of points that belong to the curve denoted by a set *E(a, b)* along with a special point at infinity, denoted by *O*. *E(a, b)* is a abelian group under a special addtion operator, denoted by *+*

### **Algebraic addition**

### *P and Q*

If I want to add a point *P* to another point *Q*, I take the following steps:

1. Draw a straight line joining points *P* and *Q*
2. Find the intersection of the joining line and the elliptic curve to get a third point R
3. Reflect the point R along the *x*-axis. It give a point denoted by *R'*.
4. Denoted: *P + Q = R'*

$$
y^2 = x^3 - 5x + 9
$$


The straight line passing through points *P* and *Q* is
$$
\\ y = \alpha x + \beta
$$

with

$$
\\ \alpha = \frac{y_Q - y_P}{x_Q - x_P}
$$

In this image, there are three intersection points between the straight line and the elliptic curve, satisfied equation under

$$
\\(\alpha x + \beta)^2 = x^3 + ax + b
$$

Two of these roots are *x*-coordinates of points *P* and *Q*, the third root (of point R) can be found using property of a monic polynomial.

$$
\\x^3 - \alpha ^ 2 x^2 + (a - 2 \alpha \beta)x + (b - \beta ^ 2) = 0
$$

By the [Viet theorem](https://www.emathhelp.net/notes/algebra-1/quadratic-equations/viet-theorem/)

$$
\\x_P + x_Q + x_R = \alpha ^ 2
$$

from which I can find the third root

$$
\\x_R = \alpha ^ 2 - x_P - x_Q
$$

In addition, *R* is a straight line passing through *P* and *Q*. So, I can express *y*-coordinate of point *R* as:

$$
\\y_R = \alpha x + \beta
$$

$$
\\y_R = \alpha x_R + (y_P - \alpha x_P) = \alpha (x_R - x_P) + y_P
$$

Result of addition of two points is the reflection of point *R* along *x*-axis

$$
\\x_{P+Q} = \alpha ^2 - x_P - x_Q
$$

$$
\\y_{P+Q} = -\alpha (x_{P+Q} - x_P) - y_P
$$

### *P and P*

ECC is based on adding a point to ifself *k* times in order to obtain another point

*k x P*. Adding point to ifself is called point doubling and expressed as *P + P = 2P*

I can compute *2P* using the following steps:

1. Draw a tangent line at *P*
2. Find the intersection of the tangent line with the elliptic curve to obtain point *R*
3. Reflect the point of intersection along the *x*-axis

$$
y^2 = x^3 - 5x + 9
$$


Point doubling can also be easily expressed algebraically. Similarly to point addition, I calculate the slope. I obtain the slope of a single point *P* at *(x, y)* by:

$$
2y\frac{dy}{dx} = 3x^2 + a
$$

and expressing the slope as:

$$
\alpha^2 = \frac{3x_P^2 + a}{2y_P}
$$

Similar to the above, I have the result:

$$
x_{2P} = \alpha ^2 - 2x_P
$$

$$
y_{2P} = -\alpha (x_{2P} - x_P) - y_P
$$

After that, I illustrate the *Point addition* algorithm on python as follows:

from collections import namedtuple
Point = namedtuple("Point", "x y")

def point_addition(P, Q):    
    if P != Q:
        lamda = (Q.y - P.y)*inverse_mod(Q.x - P.x, p)
    else:
        lamda = (3* P.x^2 + A)*inverse_mod(2*P.y, p)
    Rx = (lamda^2 - Q.x - P.x) % p
    Ry = (lamda*(P.x - Rx)- P.y) % p
    return Point(Rx, Ry)

### **Scalar Multiplication**

Scalar multiplication can represented as repeated point addition.

For example, I want to calculate *3P*. The multiplication can be represented as a series of addition:

$$
3P = P + P + P
$$

To calculate *3P*, I divide it by 2 steps.

- Addition two point the similarities:

$$
P + P
$$

- Addition two point are different:

$$
2P + P
$$

Using point addition technique described in *Algebraic addition* to obtain result.

Scalar multiplication algorithm is implemented on python like this code:

from collections import namedtuple
Point = namedtuple("Point", "x y")

def scalar_multiplication(Q, n):
    R = Point(0, 0)
    while n > 0:
        if n % 2 == 1: 
            R = point_addition(R, Q)
        Q = point_addition(Q, Q)
        n = n // 2
    return R

### **Elliptic-Curve Diffie-Hellman**

As described on [wikipeida](https://en.wikipedia.org/wiki/Elliptic-curve_Diffie%E2%80%93Hellman) Elliptic-Curve Diffie-Hellman (ECDH) is a key agreement protocol that allows **two parties**, each having an **elliptic-curve** public-private key pair, to establish a shared **secret** over an **insecure channel**. This shared secret may be directly used as a key, or to derive another key.

The key, or the derived key, can then be used to encrypt subsequent communications using **symmetric-key cipher**. It is a variant of the **Diffie-Hellman protocol** using **elliptic-curve cryptography**.

ECDH is very similar to the classical Diffie-Hellman Key Exchange (DHKE) algorithm, but it uses ECC point multiplication instead of modular exponentiations. ECDH is based on the following property of EC point:

$$
(a * G) * b = (b* G) * a
$$

Alice and Bob want to create a secure communication channel. They choose ECC parameters *p, a, b* for an Elliptic Curve and base point *G*

After that, following like this image:


### **Advanced Encryption Standard**

You can find the definition of AES on the [wikipedia](https://vi.wikipedia.org/wiki/Advanced_Encryption_Standard) or anywhere on google because it's so common.

"The algorithm was designed by two Belgian cryptographers: Joan Daemen and Vincent Rijmen. The algorithm was named "Rijdael" during the AES design competition.

Although the two names **AES** and **Rijdael** are often referred to interchangeably, in fact the two algorithms are not exactly the same. AES only works with **128/192/256bits** data blocks while Rijdael can work with data and keys of any length that is **multiple of 32bits**"

Unlike DES, AES rounds are a variable that depends on the size of the key. Plaintext is divided into blocks of size 16bytes.

Description by [link](https://www.tutorialspoint.com/cryptography/advanced_encryption_standard.htm)


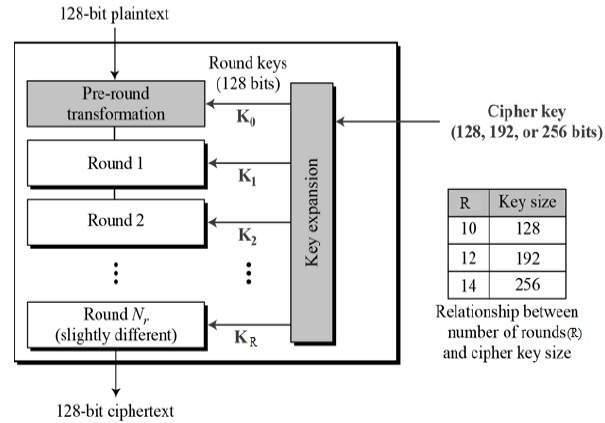
Each round consists of 4 sub-processes as shown below:


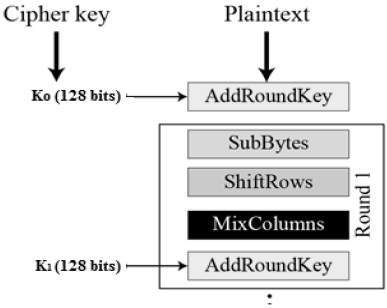
I will not go too closely into AES, I hope that readers here have a little understanding of this algorithm.

After that,I used it to encrypt the data exchanged on the communication channel.

### **Signing with ECDSA**

continue...