# Nadaraya-Watson推定 と k近傍法(1)
# はじめに
この記事は[古川研究室 Workout calendar](https://qiita.com/flab5420/private/aee38a24be700d146817) 3日目の記事です. もっちゃんに引き続き回帰の話が続きます.
今回はノンパラメトリックな回帰手法の例として, k近傍法と古川研究室で馴染深いNadaraya-Watson推定を取り扱います. また, 随時コードと実行結果を乗せて解説していきます.

# 回帰
回帰とは機械学習のタスクの一つです.

## 問題設定
given: $D$次元ベクトルの観測<font color="Red">データ</font> $\mathbf{x} \in \mathbb R^D$と<font color="Blue">ラベル</font>$y \in \mathbb R$のペア$\{{ (\mathbf{x}_n,y_n)}\}_{n=1}^N$
estimate: $y \simeq f(\mathbf{x})$となるような写像 $f$

<font color="Green">写像</font>$f$を得ることによって, 新規観測データ$\mathbf{x}^\ast$のラベル$y^\ast$を求めることができます.

### 回帰の具体例

例えば, アイスクリーム屋その日の<font color="Blue">売り上げ</font>が知りたいとします.
過去の<font color="Red">データ</font>として日毎の売上と温度・湿度・日照量があり,
売り上げと天気情報の<font color="Green">関係</font>を知ることで, 当日の天気予報から当日のアイスクリームの売上の予測をします. これが回帰の使われ方です.
一般的な回帰の問題設定は次で説明します.

#### 実装
今回は$D=1$, 真の関数を $\sin(x)$とします

import numpy as np # jypyterなら %matplotlib inline
import matplotlib.pyplot as plt

n = 20  #データ数
X_n = 1000 #任意のxの数(グラフの解像度にもなる)

x = np.linspace(-np.pi,np.pi,n)+ np.random.randn(n)/4 #データ 
t = np.sin(x) + np.random.randn(n)*0.1 # ラベル

x_star = np.linspace(-np.pi*1.5,np.pi*1.5,X_n) # 任意のx
y = np.sin(X) # 真の関数

これをプロットしたものは


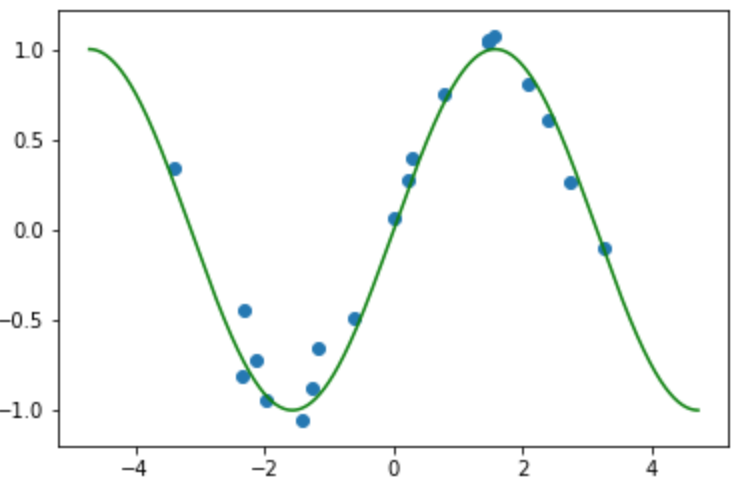
横軸はデータ$x$軸, 縦軸はラベル$y$軸の図です. 真の関数(緑線)にノイズが加わって, 入力(青点)を得ます. 真の関数がわからない中でデータとラベル集合を使って写像を推定してします.

## 回帰手法
写像$f$を求めるのに様々な手法があります.
例えば, 線形回帰では パラメータ$\mathbf w$を使って写像が$f_\mathbf{w}(\mathbf x_n) = (w_1x_{n1}+w_2x_{n2} +\dots +w_D x_{nD}) = \mathbf w^\mathrm{T} \mathbf{x}_n$として表現できると仮定し, 写像を推定する問題をパラメータ$\mathbf w$の推定問題に帰着させます. そして二乗誤差の総和を目的関数として定め, 目的関数の最適化を行いパラメータを推定します.
今回紹介するk近傍法, Nadaraya-Watson推定はパラメータを写像$f$を直接推定します.

### k近傍法
機械学習の初歩的な学習器で一般的にはクラス分類に使われる手法です.
任意の$\mathbf{x}$の$k$個の近傍のラベルを参考にして$y$を決定します. 一般には, $k$個の近傍のラベルの平均を $f(\mathbf{x})$ として, 次式で表します.

$f(\mathbf{x}) = \frac{1}{k}\tag{1} \sum_{i \in N_k(\mathbf{x})} y_i$

ここで, $N_k (\mathbf{x})$は$\mathbf{x}$からの二乗距離がもっとも小さい$k$個の点のインデックス集合を表します.

#### 実装
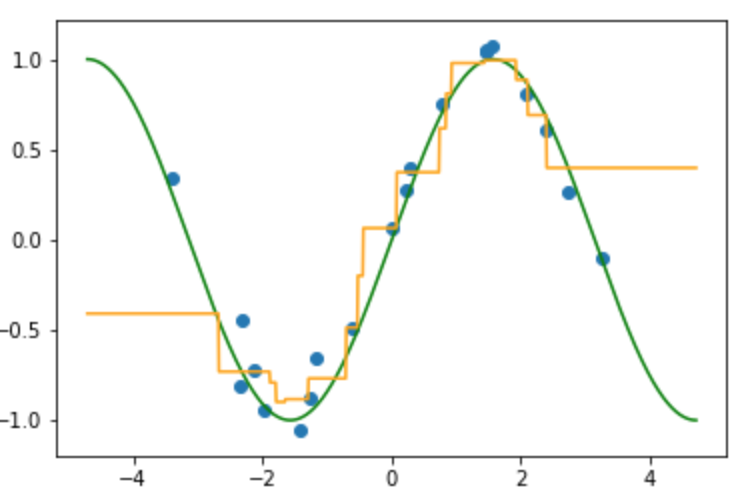
先ほどと同様に真の関数(緑線)にノイズが加わり入力(青点)が得られている状況から写像$f$(オレンジ線)を推定しています.

k = 4 # NumpyのBroad cast と fancy indexは神
Delta = x[:,None] - x_star[None,:] #データ点と任意のxを全ての差を計算
Dist = np.square(Delta) #距離として扱う
neighbor_index = np.argsort(Dist, axis=0)[:k,:] #小さい順にソートし, k個の近傍のindexを得る
Y = np.sum(t[neighbor_index],axis=0)/k #今回は平均をとる 

近傍にとる数を変えながら順次プロットしたものが以下の画像になります.

(k=4のとき)

(k=10のとき)
k の数を増やすと全体の平均に近づく. k=データ点のときは完全に平均になる.

(k=1のとき)

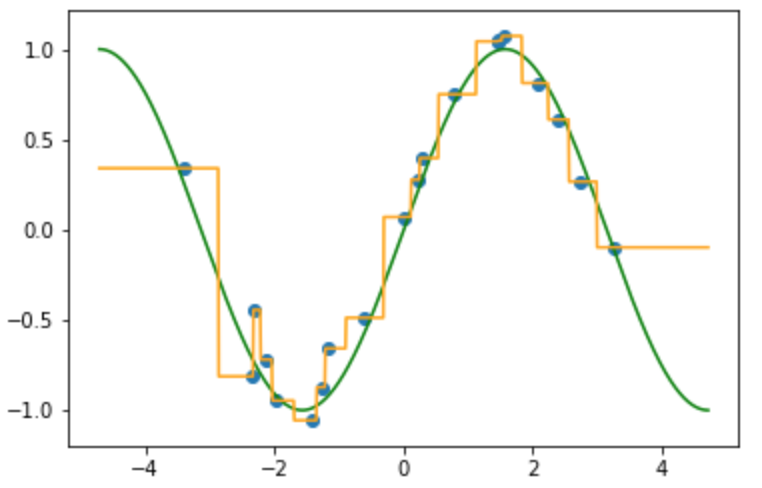
kの数1にすると, ちょうど近傍が変わる$x$は隣り合うデータの中点となる.

### まとめ

$f(\mathbf{x})$は不連続になっていて自分の精神衛生的に気持ちよくないです.
写像を滑らかにするようにとるNadaraya-Watson推定は４日後に投稿予定です. また, そこではk近傍法との関連も述べます.

## 参考文献

Trevor Hastie・Robert Tibshirani・Jerome Friedman著, 杉山 将・井出 剛 ら監訳 [「統計的学習の基礎」](https://www.amazon.co.jp/%E7%B5%B1%E8%A8%88%E7%9A%84%E5%AD%A6%E7%BF%92%E3%81%AE%E5%9F%BA%E7%A4%8E-%E2%80%95%E3%83%87%E3%83%BC%E3%82%BF%E3%83%9E%E3%82%A4%E3%83%8B%E3%83%B3%E3%82%B0%E3%83%BB%E6%8E%A8%E8%AB%96%E3%83%BB%E4%BA%88%E6%B8%AC%E2%80%95-Trevor-Hastie/dp/432012362X/ref=sr_1_1?__mk_ja_JP=%E3%82%AB%E3%82%BF%E3%82%AB%E3%83%8A&keywords=%E7%B5%B1%E8%A8%88%E7%9A%84%E5%AD%A6%E7%BF%92%E3%81%AE%E5%9F%BA%E7%A4%8E&qid=1563430788&s=gateway&sr=8-1) $\S 6$ p.220~