# Nadaraya-Watson推定 と k近傍法(後編)
この記事は[古川研究室 Workout calendar](https://qiita.com/flab5420/private/aee38a24be700d146817) 7日目の記事です.
本記事は古川研究室の学生が学習の一環として書いたものです．

一回ほとんど書いてた記事が全部消えて夜中に吠えました. 下書き保存ちゃんと押しましょう.

# 前回のおさらい
前回の記事 [Nadaraya-Watson推定 と k近傍法(前編)](https://qiita.com/kpasso1015/items/50e62ca52b4a19bfb782)では 回帰の問題設定を述べ, その回帰を解く手法の一つとしてk近傍法を解説しました。

## 回帰の問題設定
given: $D$次元ベクトルの観測データ$\mathbf{x} \in \mathbb R^D$とラベル$y \in \mathbb R$のペア $\{ ( \mathbf{x}_n,y_n )\} _{n=1}^N$
estimate: $y \simeq f(\mathbf{x})$となるような写像 $f$

## k近傍法

真の関数(緑線)にノイズが加わった入力(青点)が得られている状況で, 4個の近傍のラベルの平均として得られた写像 $f$ (オレンジ線)が以下の図になります。


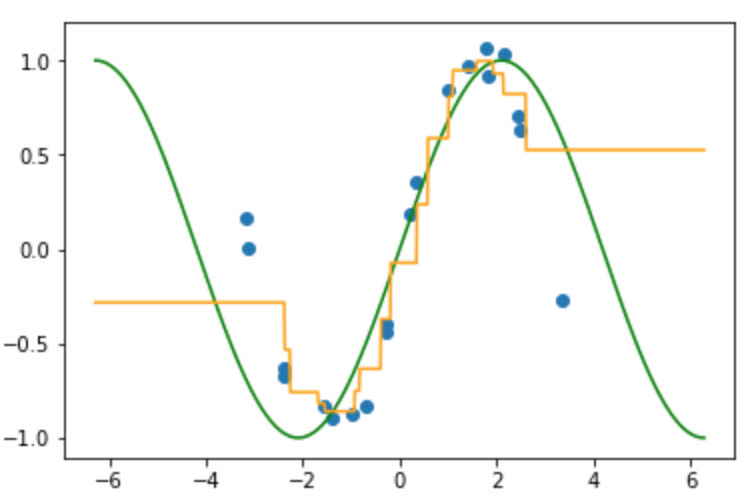
着目点(赤点線: $x=1.8$)とそこの近傍の範囲(赤線)


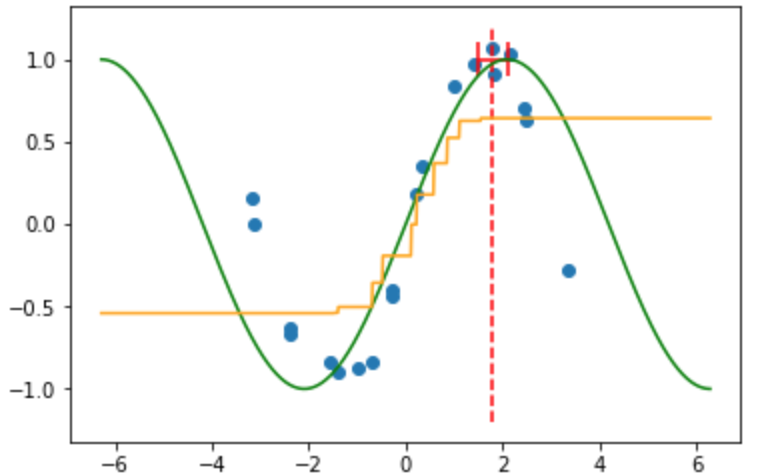
k近傍法は重みや基底関数を使わずに写像を推定していますが, その推定した写像は**不連続**な写像になっており**微分ができません**.

# Nadaraya-Watson推定

Nadaraya-Watson推定は回帰手法の一つです.

k近傍では近傍に含むデータ点に等しい重みを付与して(平均)していますが, Nadaraya-Watson推定では着目点とデータの距離に応じて滑らかに減少する重みを与えます.
Nadaraya-Watson重み付きカーネル平均はカーネル関数を使って以下の式で与えられます.

$f(\mathbf{x}) = \frac{\sum_{i=1}^N K_\lambda(\mathbf{x},\mathbf{x}_i)y_i}{\sum_{j=1}^N K_\lambda(\mathbf{x},\mathbf{x}_j)}$

今回 カーネル関数$K_\lambda(\mathbf{x},\mathbf{x_j})$は次式で与えます.

$K_\lambda(\mathbf{x},\mathbf{x_j}) = \exp(\frac{-1}{2\sigma^2}||\mathbf{x} - \mathbf{x_j}||^2)$

この式はガウス関数の式と等価です. 他のカーネル関数としてはイパネクニコフ関数や短形3次関数が一般的です.
「カーネル関数, 」と続けますと[本一冊](https://www.amazon.co.jp/%E3%82%AB%E3%83%BC%E3%83%8D%E3%83%AB%E5%A4%9A%E5%A4%89%E9%87%8F%E8%A7%A3%E6%9E%90%E2%80%95%E9%9D%9E%E7%B7%9A%E5%BD%A2%E3%83%87%E3%83%BC%E3%82%BF%E8%A7%A3%E6%9E%90%E3%81%AE%E6%96%B0%E3%81%97%E3%81%84%E5%B1%95%E9%96%8B-%E3%82%B7%E3%83%AA%E3%83%BC%E3%82%BA%E7%A2%BA%E7%8E%87%E3%81%A8%E6%83%85%E5%A0%B1%E3%81%AE%E7%A7%91%E5%AD%A6-%E8%B5%A4%E7%A9%82-%E6%98%AD%E5%A4%AA%E9%83%8E/dp/4000069713)書くのにちょうどいい分量になるので省略し, ここではカーネル関数 $K_\lambda(\mathbf{a},\mathbf{b})$は$\mathbf{a}=\mathbf{b}$のとき最大値の1をとること, $\mathbf{a}$ と$\mathbf{b}$の近さを表す値になっているということだけを押さえましょう.

##実装
k近傍法と同様の状況です.

### 近傍半径: 0.2のとき

def NW(sigma=0.2):
    global H, R, Y
    Delta = x[:,None] - x_star[None,:] #データ点と任意のx_starを全ての距離をnumpyのBroad castで計算している
    Dist = np.square(Delta)
    H = np.exp(-0.5/sigma * Dist) #近傍半径が大きいほど、距離をあまり考慮しなくなるのがわかる
    G = np.sum(H, axis=0)[None,:] 
    R = H/G
    check_sum = np.sum(R, axis=0)
    # print(check_sum)
    Y = R.T@t #(任意のx_starの数,データ数) x_star (データ数, ラベルの次元(今回は1))

sigma = 0.2 #近傍半径 
NW(sigma)

#### カーネル関数:
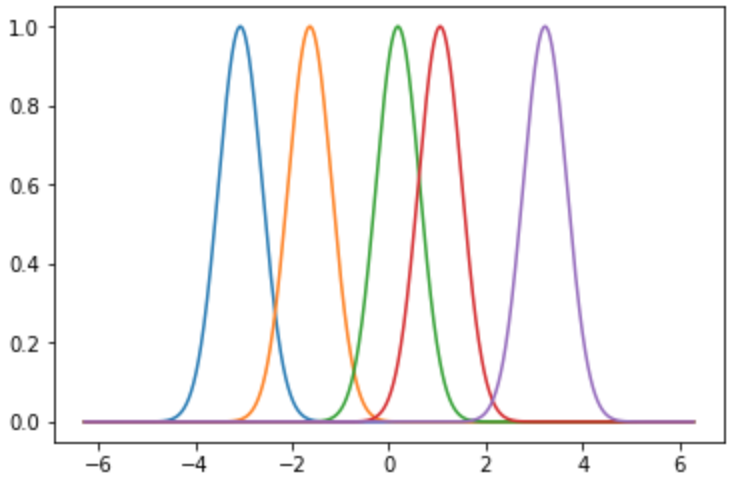
$f(\mathbf{x}) = K_\lambda(\mathbf{x},\mathbf{x}_i)$:
各データ点を中心とした近傍半径0.2のガウス関数


#### 重み付きカーネル関数:
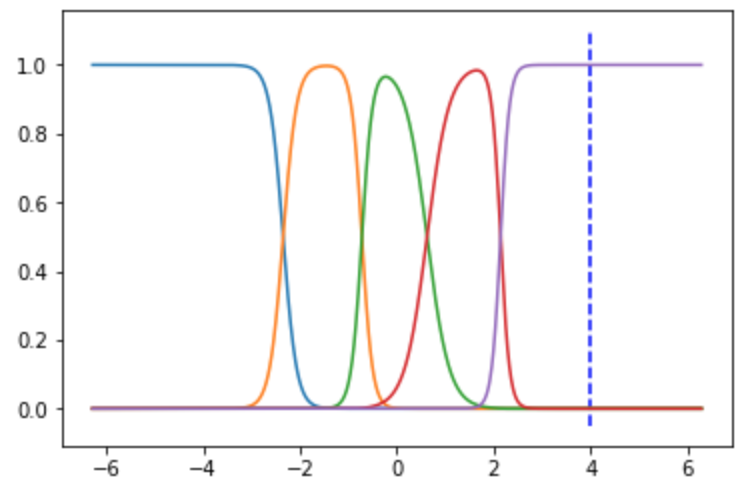
$f(\mathbf{x}) = \frac{K_\lambda(\mathbf{x},\mathbf{x}_i)}{\sum_{j=1}^N K_\lambda(\mathbf{x},\mathbf{x}_j)}$ :
任意の$x$において合計が1となるように正規化をします.
着目点(青点線 $x=4$)のときを見ていただければ, 総和が1になっていることがわかりやすいと思います.


#### 重み付きカーネル平均:
$f(\mathbf{x}) = \frac{\sum_{i=1}^N K_\lambda(\mathbf{x},\mathbf{x}_i)y_i}{\sum_{j=1}^N K_\lambda(\mathbf{x},\mathbf{x}_j)}$

先ほどのカーネル関数でそれぞれのラベルに重みをつけ, 総和をとったもの(総和が1なので重み付き平均)が推定した写像(オレンジ線)です.


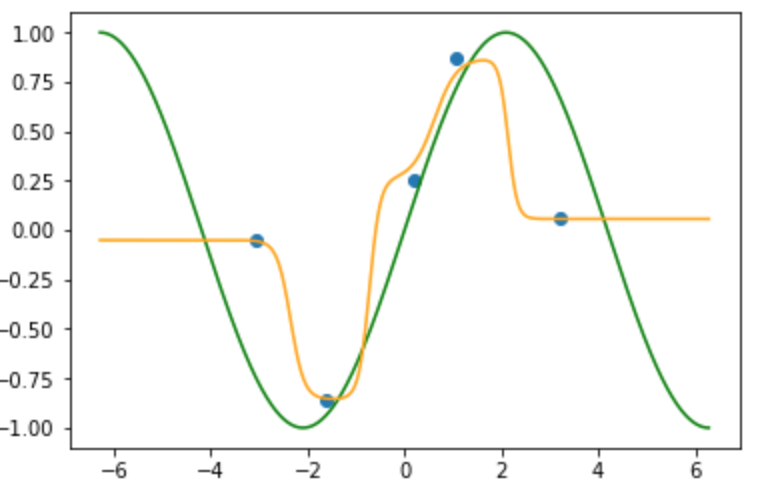
k近傍法と同様にデータの**内分点**を通り, 得られた写像は滑らかな写像になっていることが確認できます. またデータの端点以降($x > -3.0, 3.3 < x$)の写像は端点のラベルに収束しています.

### 近傍半径: 2.0のとき

近傍半径を大きくした場合, 任意の$x$ではより遠くのデータの影響を受けやすくなります.


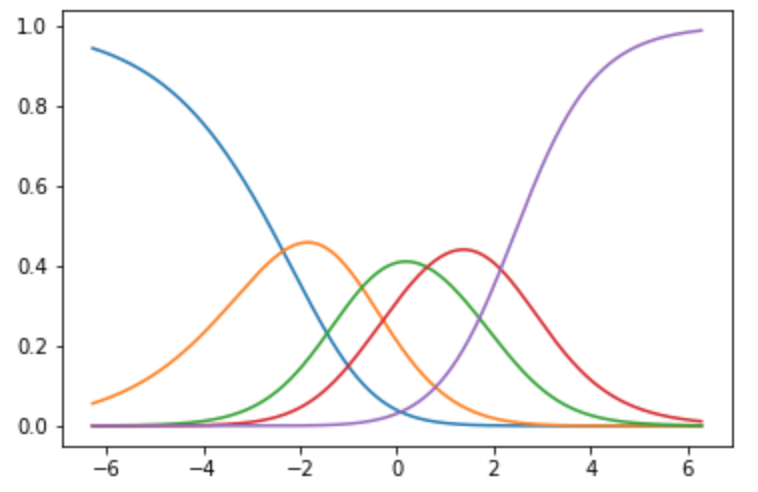
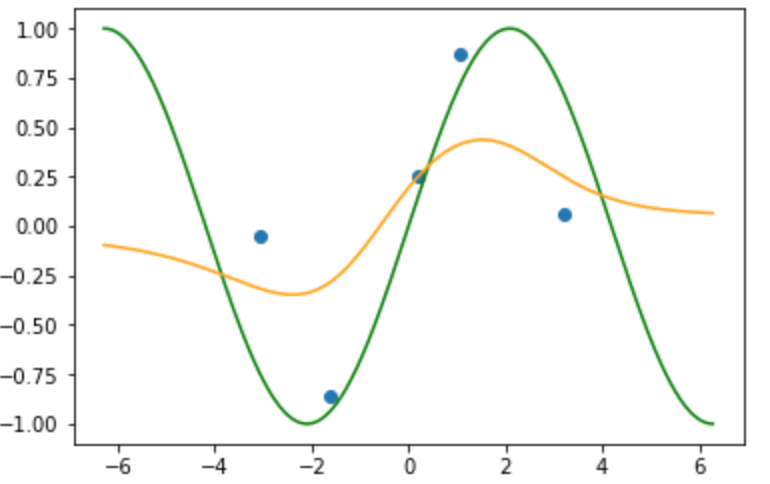
限りなく近傍半径を大きくした場合写像は単純にラベルの平均となります.

#### 近傍半径: 10000.0のとき

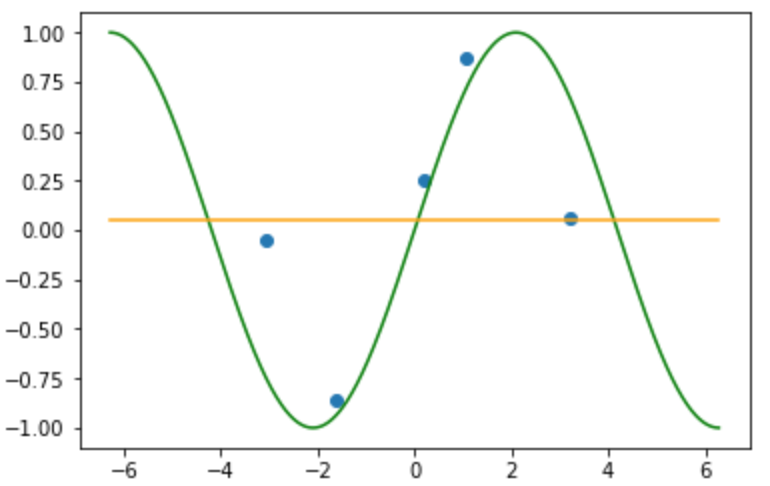
(そういえばk近傍法も$k=n$のときラベルの平均になったなあ....あれれ??)

### 近傍半径: 0.001のとき

近傍半径を小さくした場合, 任意の$x$で他のデータの影響を受けにくくなります.


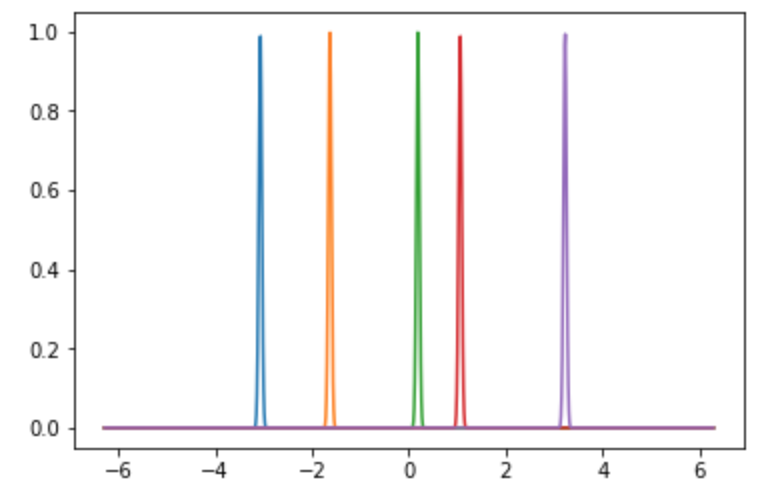
カーネル関数はデルタ関数のようになります.


任意の$x$では, ほぼ一つの点にしか重みがついてないことがわかります.

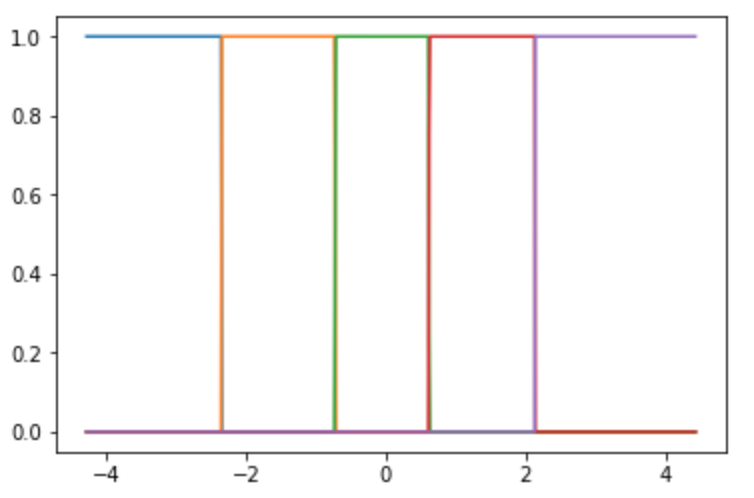
#### k近傍法(k=1)
ここで近傍法との関わりを見ていきましょう.
近傍の数が1の時の結果は以下のようになります.


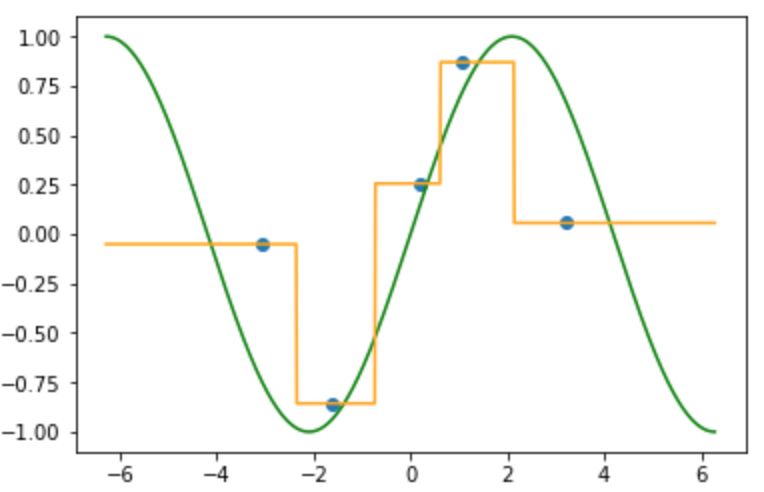
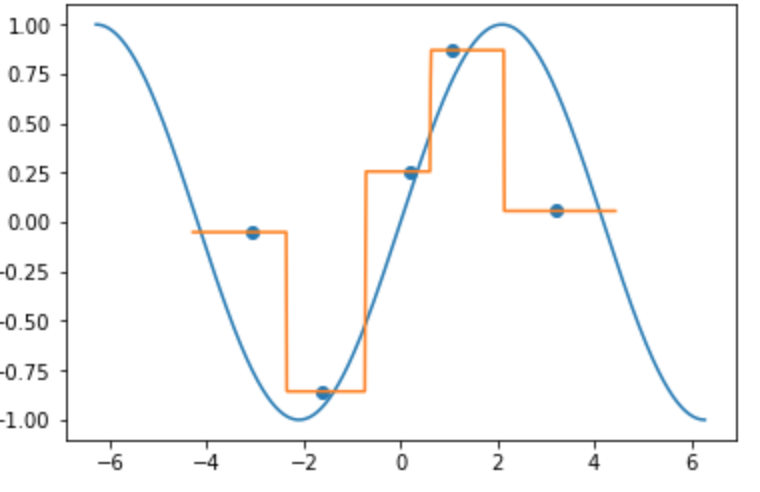
近傍半径の大きさを限りなく小さくした時と同じような結果になりました.

k近傍法をあえてカーネル回帰として捉えるならば, 近傍が変わるまでの長さが一律ではないことから, カーネル幅がカーネル関数(データ)ごとによって変わるデジタル波形のようなカーネル関数をもつカーネル回帰といえることがわかります.

## 参考文献

Trevor Hastie・Robert Tibshirani・Jerome Friedman著, 杉山 将・井出 剛 ら監訳 [「統計的学習の基礎」](https://www.amazon.co.jp/%E7%B5%B1%E8%A8%88%E7%9A%84%E5%AD%A6%E7%BF%92%E3%81%AE%E5%9F%BA%E7%A4%8E-%E2%80%95%E3%83%87%E3%83%BC%E3%82%BF%E3%83%9E%E3%82%A4%E3%83%8B%E3%83%B3%E3%82%B0%E3%83%BB%E6%8E%A8%E8%AB%96%E3%83%BB%E4%BA%88%E6%B8%AC%E2%80%95-Trevor-Hastie/dp/432012362X/ref=sr_1_1?__mk_ja_JP=%E3%82%AB%E3%82%BF%E3%82%AB%E3%83%8A&keywords=%E7%B5%B1%E8%A8%88%E7%9A%84%E5%AD%A6%E7%BF%92%E3%81%AE%E5%9F%BA%E7%A4%8E&qid=1563430788&s=gateway&sr=8-1) $\S 6$ p.220~