Changing gas cost of hash functions to match them with proving cost

Motivation

The goal of this post is to estimate the proposed coefficients in EIP-7667 for modifying the gas cost for opcodes and precompiles related to hashing in EVM.

The proposed increases in EIP-7667 for now are:

Parameter	Previous value	New value
KECCAK_BASE_COST	30	300
KECCAK_WORD_COST	6	60
SHA256_BASE_COST	60	300
SHA256_WORD_COST	12	60
RIPEMD_BASE_COST	600	600
RIPEMD_WORD_COST	120	120
BLAKE2_GFROUND	1	10

These proposed costs are based on declared proving cost, not particularly for actual usage in Ethereum. Here, we instead run zkVM prover on a set of Ethereum blocks to obtain the average proving runtime.

There is alternative workstream which measures the native execution speed for different execution clients. See the proposal.

Hash function usage in Ethereum

For the benchmarks, we looked at blocks from 21733089 to 21733759. These blocks include in total of 111373 transactions. For all these transactions, we perform execution tracing to obtain the actual hash function usage. The total gas used in the transactions is 10135367525.

Gas used for hash functions is correspondingly:

hash function	static gas	dynamic gas	total	relative %
keccak	41922120	18177390	60099510	0.5929
sha256	315900	201336	517236	0.0051
ripemd160	600	120	720	0.0000071
blake2f	0	0	0	0
total	42238620	18378846	60617466	0.5980

Top 10 hash function gas usage per target (all results):

receipent	hash gas used	total gas used
0x7a250d5630B4cF539739dF2C5dAcb4c659F2488D	1029936	155297860
0x0000000000000068F116a894984e2DB1123eB395	1077726	103484178
0x1231DEB6f5749EF6cE6943a275A1D3E7486F4EaE	1117464	201962777
0x1111111254EEB25477B68fb85Ed929f73A960582	1390110	191156989
0x881D40237659C251811CEC9c364ef91dC08D300C	1598202	201675106
0x7CFdeB2dEF0fa6810eDa0Ac17c2A4e2F9e12DB4F	2111046	430954386
0xA0b86991c6218b36c1d19D4a2e9Eb0cE3606eB48	2872530	392975602
0xdAC17F958D2ee523a2206206994597C13D831ec7	3148110	728581643
0x0000000000001fF3684f28c67538d4D072C22734	3563622	421146498
0x3fC91A3afd70395Cd496C647d5a6CC9D4B2b7FAD	5947818	672308283

Top 10 hash function gas used per sender (all results):

sender	hash gas used	total gas used
0xe93685f3bBA03016F02bD1828BaDD6195988D950	277272	25376196
0xb1b2d032AA2F52347fbcfd08E5C3Cc55216E8404	396468	65636984
0xD1Fa51f2dB23A9FA9d7bb8437b89FB2E70c60cB7	430266	55621178
0x93793Bd1f3e35a0Efd098c30e486A860A0ef7551	449118	89767278
0x654dF2b648b4E5ee2Bcc7f240Ef96B18E8DEc623	570276	55349947
0xfb7d0D001BC8D0bC998071C762BfF53EE31b725F	588696	26362806
0xC94eBB328aC25b95DB0E0AA968371885Fa516215	662508	89225747
0xae2Fc483527B8EF99EB5D9B44875F005ba1FaE13	670800	102420741
0x7830c87C02e56AFf27FA8Ab1241711331FA86F43	721230	121336249
0xf7Bd34Dd44B92fB2f9C3D2e31aAAd06570a853A6	826302	33772783

Top 10 transactions per absolute gas usage (all results):

transaction	hash gas abs	hash gas relative	total gas
0xcf37dcc1af302229b7d677137f90934ad4282406af319ccdfd2d23ede7bff610	106470	1.02988544350222	10338043
0x879920522d51d3d547f7177d1fdc703862470e3d4c302a2bccfea21e2f5388cf	107184	1.02990168255518	10407207
0x8a09f57e362cc0f0d87ac0b71b56c50bfd670de0336bb6876b3707d97c2b5549	107184	1.02644014194569	10442304
0x54c41b41f4e7fd1a7c6c163f82fc711b55d9a724e1b1c275735c79f4935719f4	118476	1.99964353564036	5924856
0x7b87d7cc4a68aa3a6f9a7cad65ac1fdf9db8e61b9cc7df46e3eb1071cdf418b6	124620	6.41851697337722	1941570
0xe9ab98d41a90660a9f8aa2a895ac6f5190169b78979893297e7b19b95bb52a6b	186072	1.76848501760387	10521548
0xf7021f65fa000a6e1fa4b78c23a2de5901de291358c9faa3bb8941eff499dedb	195678	4.75165731769505	4118100
0x4194063828fc16ea48c913eea0e2b82e44e7a5a990936131ef6aacb94ba0bb3b	211680	2.33523895215639	9064597
0x625048d6a13dbd24ed01f39e68f463bf19b7dbdddbe3a38ab5c13b427d546e7d	268764	3.45597116346426	7776801
0xa49fe3c75eec28cd1096423d2d4ec4006fe7ecc62c2b43432d9a13f215f41405	371466	2.40051429344686	15474434

Top 10 transactions per relative gas usage (all results):

transaction	hash gas abs	hash gas relative	total gas
0xf7021f65fa000a6e1fa4b78c23a2de5901de291358c9faa3bb8941eff499dedb	195678	4.75165731769505	4118100
0x2eb79011a89cb277ceb9b3fa2f134275ff2a6077e4945dee9e35bb499026548c	19332	4.88349534183457	395864
0xca9db98115f06b18f976be3b6270d9184811c51ed71d7b20803e895ec50dd30e	48120	5.04602981687694	953621
0x9d032c1a67f654eb8463d016ce17004ce07a20ae77f279aefb7f303840ed5c24	21606	5.05933703623915	427052
0xd26b0227f1d1bb8a0939e6d7860194ba04f3819736767c39d628daa740c76a8d	19206	5.06174986954253	379434
0x230702f59397640cc3b98208caac80933cb0a0a3ad56cc46e9cda5713fa76b37	33120	6.0175949242895	550386
0xf96dd26ea4d70d7fb63cf52bc62e1027d3635da94aeb53fa9270f70ffe5569aa	57540	6.30519373074829	912581
0xe3d7d9221172860bfb71cca378358e9e478ab5e03749d08d774a65a785549dc9	37806	6.39751720963604	590948
0x29df2b99ad005110174f0bebf832c429d27c620a694dac4d7c6e9534028fd2ed	37806	6.39777704070236	590924
0x7b87d7cc4a68aa3a6f9a7cad65ac1fdf9db8e61b9cc7df46e3eb1071cdf418b6	124620	6.41851697337722	1941570

Proving performance

For the same blocks, we used reth with SP1 zkVM to obtain the prover performance. We used AWS g6e.2xlarge machine with 1 GPU and 48GB GPU memory, 8CPU and 64GPU CPU memory. We used CUDA proving backend.

We currently have not benchmarked using other proof systems due to time required to set up the backends and run the provers, but are planning with the following projects:

• Risc0
• Nexus
• Valida
• Pico
• Zisk
• Jolt

Precompiles in zkVMs

In general, zkVMs compile the program into a target bytecode and then evaluate instructions one by one. This allows to prove arbitrary programs, but in case of fixed routines it is more efficient to prove the routine bytecode separately. This is implemented through zkVM precompiles, e.g. in Risc0 and SP1. In the programs, the zkVM precompiles are usually applied by patching the Rust crates which provide the primitives to be accelerated.

In the proof tests we used zkVM precompiles which were available in SP1, i.e. sha2-256, bigint, keccak, p256, bn254, bls12-381.

Proof benchmarking

For SP1, the prover reports the following time statistics:

• setup time
• proving time
• compress time

During benchmarking, we measured the full end-to-end running time. We normalize the running time against the total gas used in a block, as this allowed to compare the proving time over blocks with different gas usage.

The proving performance percentiles are (all results/all results for prove_core):

percentile	gas proven per ms
0.05	51
0.1	55
0.5	64
0.9	72
0.95	76

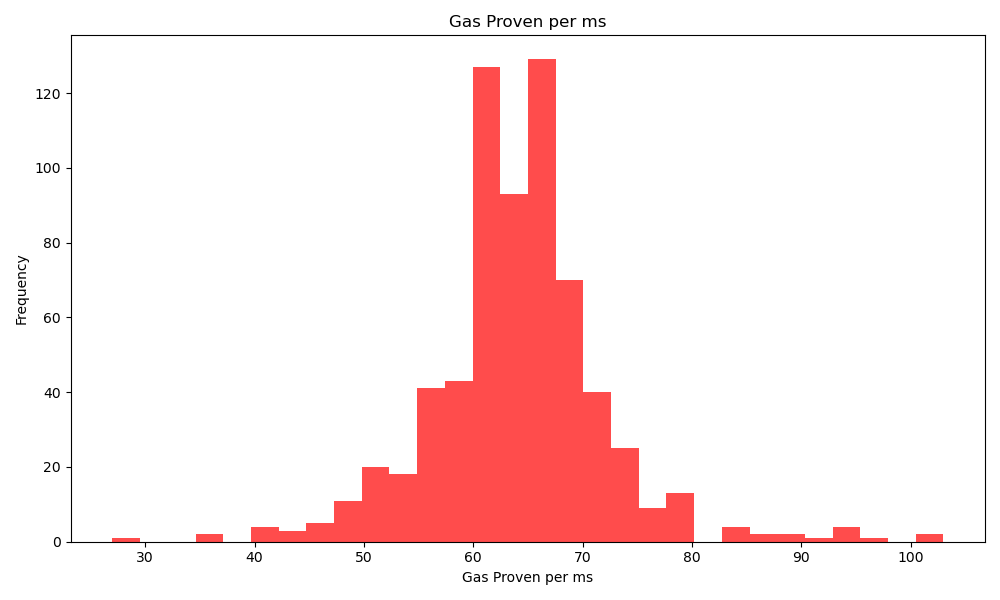
The outlier blocks with very slow proving speed seem to call KZG verification precompile at 0x0a or being small blocks. On the other hand, blocks which are very fast to prove seem to contain multiple contract creation transactions.

Hashing overhead during proving

Our first approach of estimating the hash function proving cost was to compare the block proving time with hashing opcodes being proven and not. For this, we implemented sha3-unconstrained crate which computes the Keccak permutation in SP1 unconstrained mode. The sha3-unconstrained crate is available at ivokub/RustCrypto-hashes/sha3/unconstrained. However, it is not possible to just patch the RustCrypto-hashes/sha3 crate as it would also disable proving the state accesses in EVM.

To overcome this, we also patched the revm-interpreter crate to only use sha3-unconstrained crate for the Keccak opcode. The patched crate is available at ivokub/rsp.

The overhead of Keccak proving in average blocks are (all results):

percentile	proving overhead
0.05	-0.683446
0.1	-0.338114
0.5	0.427384
0.9	1.206214
0.95	1.339756

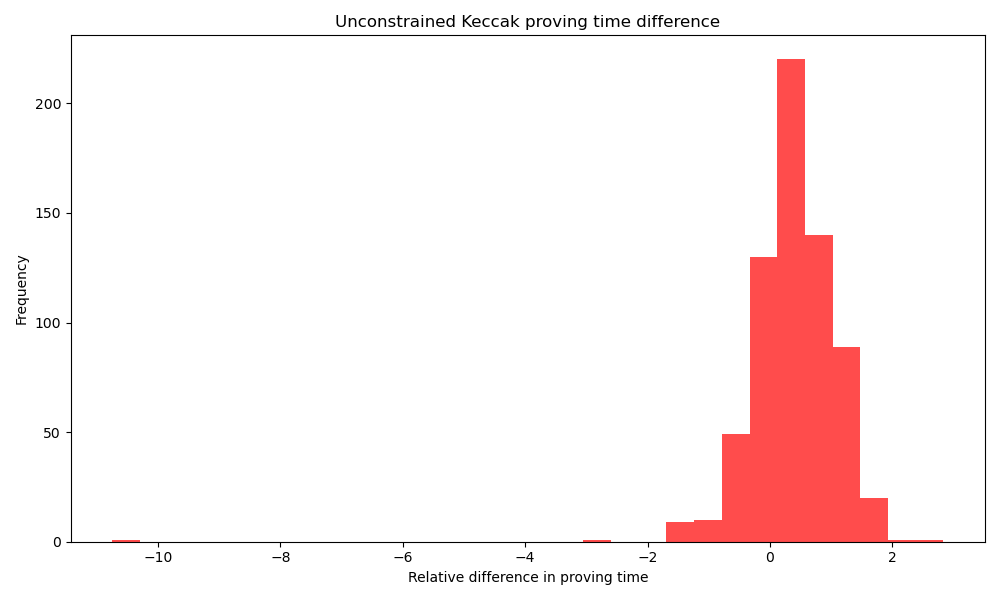
We see that the relative overhead for proving Keccak opcode for an average block is about 0.43%, but the result is not significant. There are also blocks when the proving speed seems to be faster when Keccak opcodes are proven. This seems to be due to small number of Keccak opcodes in average block and that the GPUs are not fully utilized (average utilization 75.8%) during proving. Further benchmarking could give more precise results, but it would still be very small to make any precise conclusions on the opcode mispricing, so we didn't proceed with this approach.

Worst case blocks

The second approach we took was to consider the worst-case blocks. Now, instead of looking at the proving overhead in an average blocks, we instead construct blocks with maximum number of hash calls and compare the time to prove such blocks against average block proving time.

With this approach, we want to construct blocks which spend maximum number of gas while calling the maximum number of hash function permutation. For such a block we compute the gas proven per millisecond as before when measuring the average block proving speed. From the data set the maximum gas used per block is 30141107, so we target 30M gas.

Internally, the hash function calls for Keccak, SHA2 and Ripemd-160 partition the input into blocks, which are then input into the round function together with the previous round function result. The size of the blocks is called rate. For Keccak-256 the rate is 136 bytes, and for SHA2-256 and RipeMD-160 the rates are 64 bytes. In EVM, the hash function gas cost consists of static part of calling the opcode/precompile and per-word dynamic cost. There is also misalignment in computing the dynamic cost as EVM specification counts the number of 32-byte words of inputs, which doesn't align with the actual number of rounds.

As the static cost is significantly bigger, then for creating edge-case-blocks it is better to have less opcode/precompile calls with bigger inputs. However, we also have to account for the memory expansion cost which is quadratic in the total memory usage. For benchmarking, we tested with different number of total hash calls with different input sizes to maximize the number of actual called round functions.

For Blake2f hash function the considerations are different - it doesn't provide the full hash function but only the parametrizable round function. Furthermore, there isn't a static cost but only a dynamic cost depending on the number of internal rounds.

Keccak

For Keccak opcode, we implemented the following function:

function callKeccak(uint32 nbTimes, uint32 nbBytes) public returns (bytes32) {
    assembly {
        let data := mload(0x40)
        mstore(0x40, add(data, nbBytes))
        let hash := 0
        for {let i := 0} lt(i, nbTimes) {i := add(i, 1)} {
            hash := keccak256(data, nbBytes)
        }
        mstore(0x00, hash)
        return(0x00, 32)
    }
}

We also tested with writing the implementation directly in bytecode, but the gas cost reduction was small compared to a full block and proceeded with Solidity implementation for ease of bechmarking.

With trial-and-error, the number of rounds for different inputs is:

nbBytes	nbTimes	nbRounds	gas
300000	528	1164852	29970510
100000	1589	1169579	29990437
50000	3164	1164437	29994554

For this block, the end-to-end proving time is 1254673ms, resulting in 23 gas proven per millisecond.

SHA2-256

For SHA2 precompile, we implemented the following function:

function callSha2(uint32 nbTimes, uint32 nbBytes) public returns (bytes32) {
    assembly {
        let data := mload(0x40)
        mstore(0x40, add(data, nbBytes))
        let hash := 0
        for { let i := 0 } lt(i, nbTimes) { i := add(i, 1) } {
            let success := staticcall(gas(), 0x02, data, nbBytes, 0x00, 32)
            if eq(success, 0) {
                revert(0, 0)
            }
            hash := mload(0x00)
        }
        mstore(0x00, hash)
        return(0x00, 32)
    }
}

The number of round function calls for different inputs:

nbBytes	nbTimes	nbRounds	gas
300000	264	1237633	29990838
200000	397	1241023	29995760
100000	793	1239460	29994972

The proving time for such a block is 1297880ms, leading to 23 gas per millisecond.

RipeMD-160

For RipeMD-160 precompile, we implemented the following function:

function callRipemd(uint32 nbTimes, uint32 nbBytes) public returns (bytes32) {
    assembly {
        let data := mload(0x40)
        mstore(0x40, add(data, nbBytes))
        let hash := 0
        for { let i := 0 } lt(i, nbTimes) { i := add(i, 1) } {
            let success := staticcall(gas(), 0x03, data, nbBytes, 0x00, 32)
            if eq(success, 0) {
                revert(0, 0)
            }
            hash := mload(0x00)
        }
        mstore(0x00, hash)
        return(0x00, 32)
    }
}

As there are no RipeMD-160 zkVM precompiles, then we measured the parameters which would maximize the total number of cycles to be proven inside zkVM:

nbBytes	nbTimes	nbRounds	gas
100000	79	367166790	29738766
50000	159	369876668	29980861
20000	395	370096560	29980861

With padding, this corresponds to in total of 123635 rounds.

The proving time for this block is 201890ms, leading to 148 gas per millisecond.

Blake2f

The Solidity functions for calling the Blake2f function are defined as:

function blake(uint32 rounds, bytes32[2] memory h, bytes32[4] memory m, bytes8[2] memory t, bool f) public returns (bytes32[2] memory) {
    bytes32[2] memory output;
    bytes memory args = abi.encodePacked(rounds, h[0], h[1], m[0], m[1], m[2], m[3], t[0], t[1], f);
    assembly {
        if iszero(staticcall(not(0), 0x09, add(args, 32), 0xd5, output, 0x40)) {
            revert(0, 0)
        }
    }

    return output;
}

function callBlake(uint32 rounds) public returns (bytes32[2] memory) {
    bytes32[2] memory h;
    h[0] = hex"48c9bdf267e6096a3ba7ca8485ae67bb2bf894fe72f36e3cf1361d5f3af54fa5";
    h[1] = hex"d182e6ad7f520e511f6c3e2b8c68059b6bbd41fbabd9831f79217e1319cde05b";
    bytes32[4] memory m;
    m[0] = hex"6162630000000000000000000000000000000000000000000000000000000000";
    m[1] = hex"0000000000000000000000000000000000000000000000000000000000000000";
    m[2] = hex"0000000000000000000000000000000000000000000000000000000000000000";
    m[3] = hex"0000000000000000000000000000000000000000000000000000000000000000";
    bytes8[2] memory t;
    t[0] = hex"0300000000000000";
    t[1] = hex"0000000000000000";
    bool f = true;
    return blake(rounds, h, m, t, f);
}

The case of Blake2f is most complicated as it doesn't expose the full hash function, but rather only the configurable round function. One of the parameters which can be provided to the precompile is the number of internal rounds on 4 bytes. For the Blake2b the number of rounds used is 12, but in the precompile we could potentially define it as high as 4294967295. To fit inside the 30M gas limit, we used the value 29000000 which results in using 29025975 gas. As SP1 doesn't have Blake2f as a zkVM precompile, then we measured the number of cycles and it is 17322114713.

We weren't able to run end-to-end prover for this block, the GPU prover ran out of memory during the compress step. However, when we look at only prove_core step, then it took 5564000ms, leading to 5 gas proven per ms. We can compare it to the average-block prove_core time which is 93gas per ms (5%, 10%, 90%, 95% percentiles 77, 83, 105, 111 correspondingly).

Conclusions

Considering the benchmarking results, we see that Keccak opcode and SHA2 precompile are somewhat underpriced. RipeMD160 precompile seems to be overpriced. Finally, the Blake2f precompile seems to be significantly underpriced.

For Keccak and SHA2, they are about 2.78x underpriced compared to the proving cost. A conservative recommendation is to increase the dynamic gas cost for both of them by 3 (ceil(64/23)) times and larger coefficient can be considered to account for less-efficient zkVMs. The static gas cost can be smaller, as for zero-length inputs it would be possible to hardcode the hashing result and avoid proving the hash. For non-zero-length inputs the dynamic cost would account for the price increase already.

For RipeMD-160, the already proposed keeping the gas price seems on line with the actual proving time.

For Blake2f, the minimal conservative recommendation is to increase the per-round dynamic gas cost by at least 19 times (ceil(93/5)). Additionally, the precompile should limit the maximum number of rounds allowed to avoid denial of service attacks when the Ethereum gas limits are increased. In practice, the hash functions using Blake2f use 12 internal rounds.

Parameter	Previous value	Updated proposal
KECCAK_BASE_COST	30	90
KECCAK_WORD_COST	6	18
SHA256_BASE_COST	60	180
SHA256_WORD_COST	12	36
RIPEMD_BASE_COST	600	600
RIPEMD_WORD_COST	120	120
BLAKE2_GFROUND	1	19

As already mentioned, Keccak opcode should compute the dynamic gas cost based on the number of actual permutation calls for hashing the full input. Currently the dynamic cost increases after every 32 bytes, even if the number of actual permutations is the same. Better aligning the cost with number of permutations would allow using Keccak opcode more efficiently, for example when it is used for set membership, where it would be possible to use wider trees.