# 3 Statistika (WIP)

###### tags: `řsss-základ`, `matika`, `mv013`

> Statistika. Popisná statistika (charakteristiky polohy a variability, pořádkové statistiky, statistiky asociace, související grafy). Diskrétní a spojité náhodné veličiny (NV). Náhodný výběr. Parametrické pravděpodobnostní modely (distribuce) NV. Centrální limitní věta. Princip věrohodnosti, bodové a intervalové odhady. Statistická inference - testování hypotéz, hladina významnosti, koeficient spolehlivosti. Testování hypotéz na jednom vzorku, dvou vzorcích, více než dvou vzorcích (včetně jednovýběrových, dvouvýběrových a párových t-testů, ANOVA a post-hoc testů), testů dobré shody. Lineární regresní model. (MV013)
---
:::success
**Vzorce** a **formálne definície**.
:::

> **Vzorce** a **definície**
> [color=green]

:::info
**Voľné definície** a **vysvetlenia**.
:::

> **Vysvetlenie**
> [color=#0047AB]

> **Príklad**
> [color=purple]

:::warning
:book: Zdroj, ďalšie čítanie
:::

<style>
blockquote span {color:#333;}
blockquote blockquote span {color:#333;}
span.color.fa-tag {display: none;}
</style>

Takto `*[MV013]` sú označené pojmy, ktoré nie sú v zadaní otázky, no preberali sa na MV013 a môžu sa zísť.

---

> Disclaimer: poznámky sú z veľkej miery prevzaté z [materiálov](https://hackmd.io/@uizd-suui/ryQrtIvzU) vypracovaných študentami umelej inteligencie a spracovania dát na podzim 2020.

---

:::info
**Statistika** je vědní obor, který se zabývá sběrem, organizací, analýzou, interpretací a prezentací empirických dat za účelem prohloubení znalostí určité oblasti, obvykle hromadného jevu.
:::

## Popisná štatistika

:::info
**Popisná štatistika** (ako počitateľné podstatné meno) je **štatistika**, ktorá kvantitatívne popisuje alebo sumarizuje vlastnosti nejakej sady dát, zatiaľ čo popisná štatistika (ako nepočitateľný pojem) predstavuje **proces** používania a analýzy týchto popisných štatistík.
:::

:::info
:bulb: Popisná štatistika sa od **inferečnej štatistiky** líši cieľom **zhrnúť, resp. popísať** vzorku dát **namiesto odvodzovania poznatkov** o populácii, ktorú reprezentuje daná vzorka.
:::

**Typy premenných**
- číselné
- kategorické
- nominálne (neexistuje usporiadanie), napr. farba očí, pohlavie, ...
- ordinálne (existuje usporiadanie), napr. známka v škole, bodovanie

> _Má zmysel daná charakteristika pre daný typ premennej?_
>
> | charakteristika | číselná | nominálna | ordinálna |
> | --------------- | ------- | --------- | --------- |
> | priemer | :heavy_check_mark: | :x: | :x: |
> | medián | :heavy_check_mark: | :x: | |
> | modus | :heavy_check_mark: | :heavy_check_mark: | :heavy_check_mark: |
> | kvantil | :heavy_check_mark: | :x: | |
> | rozptyl | :heavy_check_mark: | :x: | :x: |
> | smerodajná odchýlka | :heavy_check_mark: | :x: | :x: |
> | Giniho koeficient| | :heavy_check_mark: | :heavy_check_mark: |
> | entropia | | :heavy_check_mark: | :heavy_check_mark: |

### Charakteristiky polohy

> Typická hodnota, ktorá vystihuje danú sadu hodnôt. Niektoré môžu byť vhodnejšie (viac výstižné) než iné.
> [color=#0047AB]

#### Aritmetický priemer (_mean_) $\bar{x}$

> Súčet hodnôt delený počtom hodnôt.
> [color=#0047AB]

:::success
$\bar{x} = \frac{1}{n} \sum^{n}_{i=1}{x_i}$
:::

- Ľahko ovplyvniteľný extrémnymi hodnotami, možné riešenia: `*[MV013]`
- _trimmed mean_ = priemer po odstránení určitého počtu extrémnych hodnôt (používa sa napr. pri športoch, ktoré sú hodnotené porotou -- najnižšie a najvyššie skóre sa zruší, výsledok je priemer zostávajúcich hodnôt),
> **Príklad:** hodnoty 7, 11, 2, 6, 14 $\rightarrow$ usporiadané 2, 6, 7, 11, 14
> $0.2$-trimmed mean = TODO
> [color=purple]
- _winsorized mean_ = priemer po nahradení určitého počtu extrémnych hodnôt menej extrémnymi (najbližšou hodnotou zo sady).
> **Príklad:** TODO
> [color=purple]

#### Medián (_median_) $\widetilde{x}$

> Hodnota nachádzajúca sa presne v polovici **zoradeného** zoznamu hodnôt.
> [color=#0047AB]

:::success
$\widetilde{x} = x_{(\frac{n+1}{2})}$ pre nepárne (liché) $n$, $\widetilde{x} = \frac{x_{(\frac{n}{2})} + x_{(\frac{n}{2}+1)}}{2}$ pre párne (sudé) $n$.
:::

- Ak je počet hodnôt párny (sudý), neexistuje jedna hodnota, ktorá by bola presne v polovici $\rightarrow$ počíta sa priemer z dvoch hodnôt.
- Vhodnejšia charakteristika polohy ako priemer v prípade _skewed_ dát.
- :bulb: $0.5$-kvantil

#### Modus (_mode_)

> Hodnota, ktorá sa v sade hodnôt vyskytuje najčastejšie, nemusí byť určená jednoznačne.
> [color=#0047AB]

- :bulb: Vhodná charakteristika aj pre kategorické premenné.

#### Kvantil (_quantile_)

> Hodnota, ktorá je väčšia alebo rovná ako $\alpha \cdot 100$ % hodnôt zo sady.
> [color=#0047AB]

:::success
$q_\alpha = x_{(\lceil n\alpha \rceil)}$
:::

- $q_{0.5}$ = medián
- $q_{0.25}$ = 1. kvartil ($Q_1$)
- $q_{0.75}$ = 3. kvartil ($Q_3$)
- $q_{0.75} - q_{0.25}$ = kvartilová odchýlka ($IQR$ = _interquartile range_)

### Charakteristiky variability

#### Rozptyl (_variance_)

> Priemer zo súčtu štvorcov (_sum of squares_).
> [color=#0047AB]

:::success
$s^2 = \frac{1}{n-1}\sum^{n}_{i=1}{(x_i-\bar{x})^2}$
:::

#### Smerodajná odchýlka (_standard deviation_)

> Odmocnina z rozptylu.
> [color=#0047AB]

:::success
$s = \sqrt{\frac{1}{n-1}\sum^{n}_{i=1}{(x_i-\bar{x})^2}}$
:::

### Charakteristiky tvaru `*[MV013]`

#### Koeficient šikmosti (_skewness_) `*[MV013]`


> - **Šikmosť $= 0$** značí, že hodnoty náhodnej veličiny sú rovnomerne rozdelené vľavo a vpravo od strednej hodnoty.
> - **Šikmosť $> 0$** značí, že vpravo od priemeru sa vyskytujú odľahlejšie hodnoty než vľavo (rozdelenie má tzv. pravý chvost) a väčšina hodnôt sa nachádza blízko vľavo od priemeru.
> - Pre **šikmosť $<0$** platí opak.
> - **Symetrické** rozdelenia (vrátane normálneho) majú **šikmosť $= 0.$**
> - Pre rozdelenia s kladnou šikmosťou obvykle platí, že modus je menší ako medián a ten je menší ako stredná hodnota (pre zápornú šikmosť naopak).
> [name=Wikipedia][color=#0047AB]

#### Koeficient špicatosti (_kurtosis_) `*[MV013]`


> - **Špicatosť $> 0$** značí, že **väčšina hodnôt** náhodnej veličiny leží **blízko** jej **strednej hodnoty** a hlavný vplyv na rozptyl majú málo pravdepodobné odľahlhé hodnoty. Krivka hustoty je špicatejšia než pri nomrálnom rozdelení.
> - **Špicatosť $< 0$** značí, že rozdelenie je **rovnomernejšie** a krivka jeho hustoty je viac plochá než pri normálnom rozdelení.
> - Normálne rozdelenie má špicatosť $= 0$.
> - Špicatosť rozdelenia nezávisí od lineárnej transformácie náhodnej veličiny, je teda napr. rovnaká pre všetky normálne rozdelenia.
> [name=Wikipedie][color=#0047AB]

### Poriadkové štatistiky (výberové charakteristiky dané poradím)

:::warning
:book: http://kfe.fjfi.cvut.cz/~limpouch/sigdat/statodn/node5.html
:book: http://user.mendelu.cz/drapela/Statisticke_metody/teorie%20text%20II.pdf
:::

:::info
**Pořádková statistika** = vzestupně uspořádané prvky souboru $x_{(1)}, x_{(2)}, \ldots, x_{(n)}$.
:::

:::danger
:warning: Úprimne netuším, čo sem patrí. Mohli by to byť štatistiky, ktoré sú založené na poradí, tj. napr. medián a kvantil, alebo by to mohli byť nejaké zložitejšie štatistiky (_rank statistics_?).
:::

### Štatistiky asociácie

:::info
Štatistiky asociácie sú faktory alebo koeficienty, ktoré **kvantifikujú vzťah** medzi dvoma alebo viacerými veličinami.
:::

#### Kovariancia

:::success
Nech $x = (x_1, \ldots, x_n)^T$ a $y = (y_1, \ldots, y_n)^T$.

**Kovariancia** $c$ je definovaná nasledovne:

$$
c = \frac{1}{n-1}\sum^{n}_{i=1}{(x_i-\bar{x})(y_i-\bar{y})}
$$
:::
> Od každého prvku výberu $x$ odčítame výberový priemer $\bar{x}$, od každého prvku výberu $y$ odčítame výberový priemer $\bar{y}$, rozdiely medzi sebou podľa indexov vynásobíme ($(x_1-\bar{x})\cdot(y_1-\bar{y})$, $(x_2-\bar{x})\cdot(y_2-\bar{y})$ atď.), výsledné súčiny sčítame a vydelíme $n-1$.
> [color=#0047AB]
> Vzorec predpokladá, že výbery $x$ a $y$ majú rovnakú veľkosť $n$.

> Ak je $c>0$, obe premenné sa menia rovnakým smerom (ak rastie jedna, rastie aj druhá a naopak).
> Ak je $c<0$, premenné sú nepriamo úmerné.
> Ak je $c=0$, premenné sa neovplyvňujú.
> [color=#0047AB]

#### Korelácia

> :bulb: **Normalizovaná** kovariancia.
> [color=#0047AB]

:::success
Nech $x = (x_1, \ldots, x_n)^T$ a $y = (y_1, \ldots, y_n)^T$.

**Korelácia** $r$ je definovaná nasledovne:

$$
r = \frac{\sum^{n}_{i=1}{(x_i-\bar{x})(y_i-\bar{y})}}{\sqrt{\sum^{n}_{i=1}{(x_i-\bar{x})^2} \sum^{n}_{i=1}{(y_i-\bar{y})^2}}}
$$
:::
> Korelácia sa počíta podobne ako kovariancia, ale čitateľ sa delí odmocninou zo súčinu **súčtu štvorcov** (_sum of squares_) pre $x$ a pre $y$.
> [color=#0047AB]

> Hodnota $r > 0.8$ znamená silný pozitívny lineárny vzťah, $r < -0.8$ silný negatívny lineárny vzťah a $r = 0$ značí, že medzi veličinami neexistuje lineárny vzťah.
> [color=green]

> Interpretácie korelácie v prírodných vedách:
> $|\rho| \in \langle0;0,4)$ - malá alebo žiadna korelácia
> $|\rho| \in \langle0,4;0,6)$ - slabá korelácia
> $|\rho| \in \langle0,6;0,8)$ - stredná korelácia
> $|\rho| \in \langle0,8;1)$ - silná korelácia
> [color=#0047AB]

>Korelácia predstavuje kovarianciu na škále $\langle- 1;1\rangle$.
> [color=#0047AB]

#### Matica korelácie (kovariancie)

:::danger
:construction_worker: TODO
:::

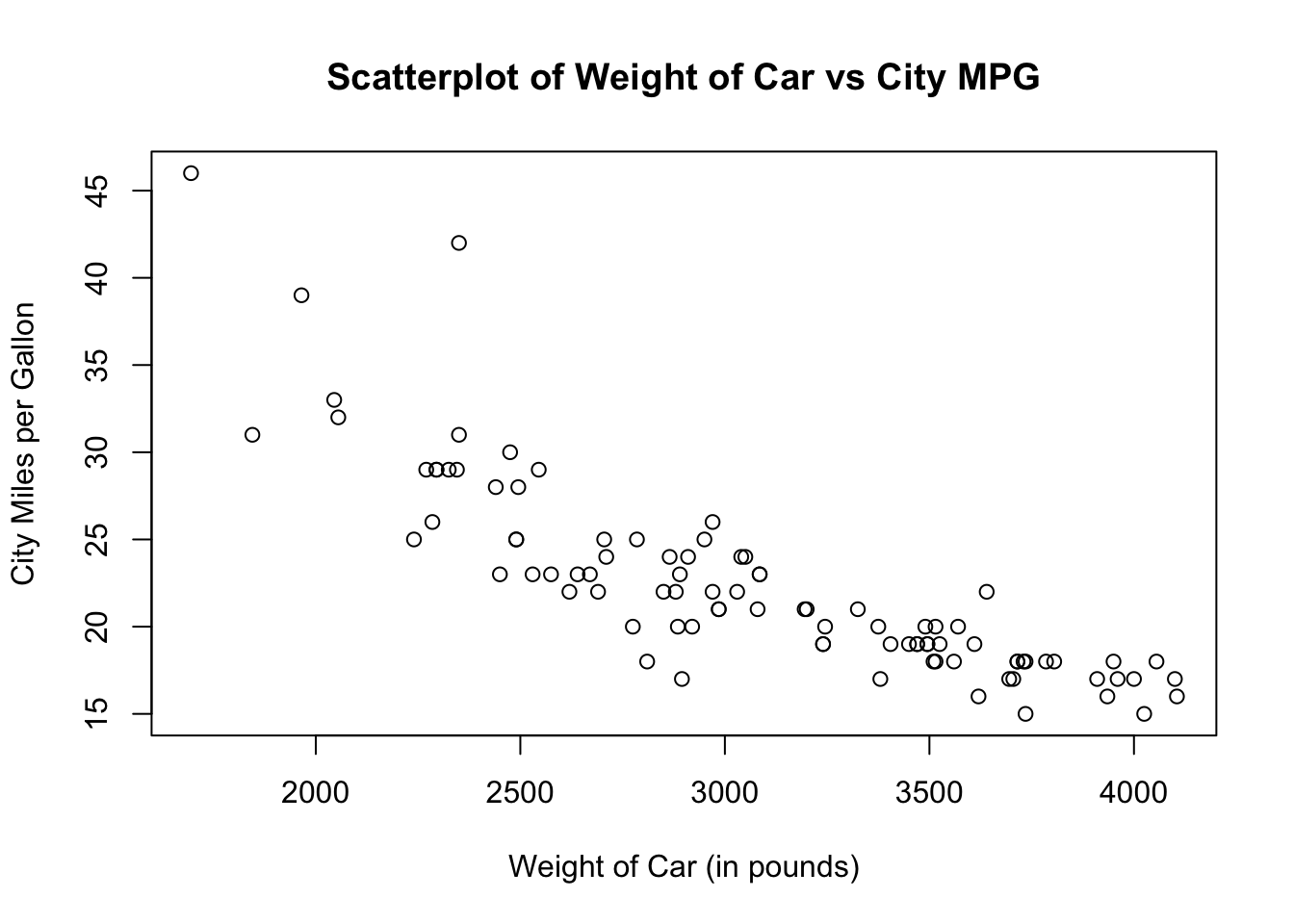
#### Scatterplot

> Vizualizuje hodnoty dvoch premenných v 2D priestore. Využíva sa na sledovanie vzťahov medzi premennými.
> V prípade, že sa scatterplot používa na zobrazenie korelácie medzi premennými, zvykne sa do grafu priložiť krivka, ktorá reprezentuje tento vzťah.
> [color=#0047AB]


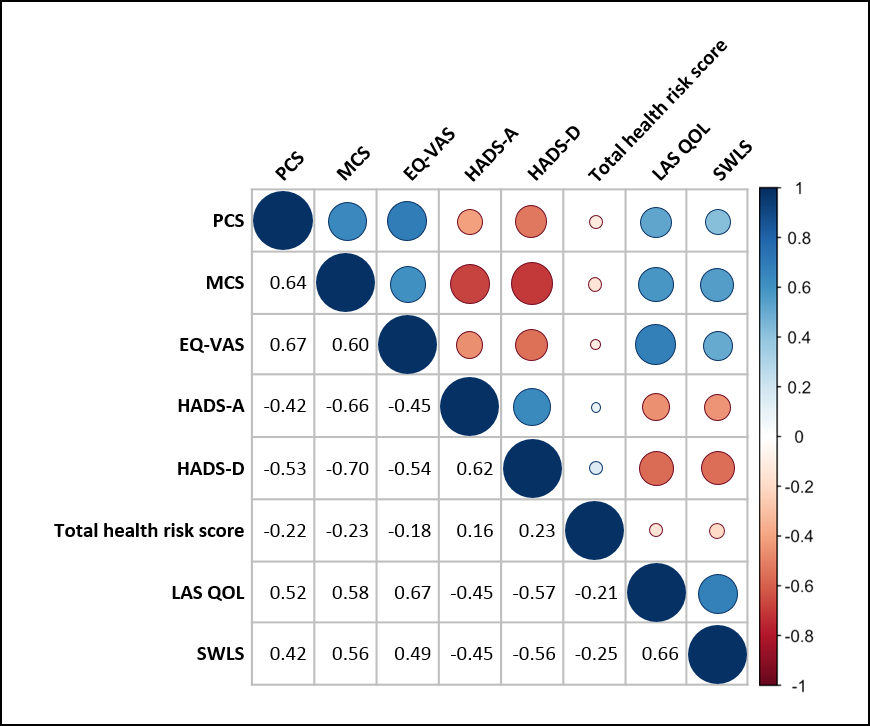
#### Korelogram
> Vizualizuje maticu korelácie. Užitočné pri veľkom počte premenných.
> [color=#0047AB]

Jedna z variánt korelogramu:

### Používané grafy
#### Boxplot

> Boxplot delí dáta na sekcie obsahujúce približne 25 % dát v dátovom súbore. Poskytujú vizuálnu sumarizáciu, vďaka ktorej je jednoduché rýchle určiť priemer, šikmosť dát, kvantily a extrémne hodnoty (outliers).
> [color=#0047AB]


## Náhodná veličina (_random variable_)

:::info
> **Náhodná veličina** je ľubovolná veličina, ktorú je možné opakovane merať a jej hodnoty spracovať metódami pravdepodobnosti alebo štatistiky. Tieto hodnoty sú pred vykonaním experimentu, resp. pozorovania neznáme.
> [name=Wikipédia][color=lightblue]

>**Náhodná veličina** je funkcia, ktorá priraďuje každému elementárnemu náhodnému javu nejakú (spravidla číselnú) hodnotu.
> [name=Wikipédia][color=lightblue]
:::

:::success
> Nech $(\Omega, \mathcal{A}, P)$ je pravdepodobnostný priestor. **Náhodná veličina** je merateľné priradenie $X: \Omega \rightarrow \mathbb{R}$.
> [name=MV013, 3. prednáška][color=green]

- $\Omega$ = neprázdna množina
- $\mathcal{A}$ = $\sigma$-algebra nad $\Omega$
- $P$ = pravdepodobnostné ohodnotenie nad $\mathcal{A}$
:::

> **Príklady:**
> [color=purple]
> - počet hláv pri 10-krát opakovanom hode mincou,
> - počet dopravných nehôd za deň,
> - doba čakania na autobus,
> - výška náhodne vybraného študenta.

Náhodná veličina môže byť **diskrétna** alebo **spojitá**.

:::warning
:book: [Wikipedie: Náhodná veličina](https://cs.wikipedia.org/wiki/N%C3%A1hodn%C3%A1_veli%C4%8Dina)
:book: https://www.statlect.com/fundamentals-of-probability/random-variables
:::

### Diskrétna náhodná veličina

:::success
Náhodná veličina je **diskrétna**, ak sa prvky výberového priestoru $\Omega$ zobrazia na os reálnych čísel ako izolované body, označené $x_1, x_2, ..., x_k$, pričom každý z týchto bodov má nenulovú pravdepodobnosť.

Pravdepodobnosť, že diskrétna náhodná veličina $X$ bude mať po vykonaní náhodného pokusu hodnotu $x$, značíme $P(X=x)$ alebo $P(x)$.

Výsledkom jedného náhodného pokusu bude, že náhodná veličina bude mať práve jednu hodnotu. **Súčet pravdepodobností všetkých možných hodnôt $x$ diskrétnej náhodnej veličiny $X$ je rovný 1**.

$$
\sum_x{P(x)} = 1
$$
:::

:::info
**Diskrétnou náhodnou veličinou** je teda všetko, čo môže nadobudnúť len jednotlivé hodnoty z konečného alebo nekonečného intervalu, tzn. **môže sa zmeniť len po skokoch**.
:::

> **Príklad**: pravdepodobnosť hodu kockou -- kocka vie nadobudnúť len hodnoty od 1 po 6.
> [color=purple]

:::success
Rozdelenie pravdepodobnosti diskrétnej náhodnej veličina sa vyjadrí tak, že sa určí pravdepodobnosť $P(x)$ pre všetky $x$ z definičného oboru veličiny $X$. Pravdepodobnosti týchto hodnôt sú vyjadrené funkciou $P(x)$, ktorá sa nazýva **pravdepodobnostnou funkciou**

Platí, že vo výberovom priestore **majú prvky súčet svojich pravdepodobností rovný 1**.
:::

> Hodnoty pravdepodobnostnej funckie sa často vyjadrujú tabuľkou. **Príklad**:
> [color=purple]
>| $x$ | $P(x)$ |
>|-----|------|
>| $x_1$ | 0,2|
>| $x_2$ | 0,3|
>| $x_3$ | 0,5|

> Pravdepodobnostnú funkciu vieme **využiť k výpočtu pravdepodobnosti**. Napríklad pravdepodobnosť, že náhodná veličina $X$ leží medzi hodnotami $x_1$ a $x_2$ môže byť vyjadrená ako $P(x_1 \leq X \leq x_2) = \sum_{x=x_1}^{x_2}{P(x)}$, čo znamená, že **sčítame pravdepodobnosti nadobudnutia hodnôt v danom rozsahu**.
> [color=#0047AB]

>**Rozdelenie početnosti diskrétnej náhodnej veličiny:**
>

:::success
Pomocou pravdepodobnostnej funkcie je možné zaviesť **distribučnú funkciu** vzťahom

$$
F(x) = P(X < x)
$$

Distribučná funkcia je **neklesajúca** a **spojitá sprava**. Hodnoty distribučnej funkcie ležia v rozsahu $0 \leq F(X) \leq 1$. Pre diskrétnu náhodnú veličinu $X$ je možné pre ľubovoľné reálne číslo $x$ vyjadriť distribučnú funkciou vzťahom

$$
F(x) = \sum_{t\leq x}{P(t)}
$$
:::

:::success
Pre popis diskrétnych náhodných veličín sa používajú rôzne charakteristiky. Jednou z najdôležitejších je **stredná hodnota** označená ako $E(X)$, ktorá je definovaná nasledujúcim vzorcom

$$
E(X) = \sum_{x_k}{x_k}P(X = x_k)
$$

**Rozptyl** náhodnej veličiny sa znači $D(X)$ a **vyjadruje veľkosť odchyliek hodnôt náhodnej veličiny od jej strednej hodnoty**. Vyjadruje sa ako

$$
D(X) = \sum_{x_k}{x_k^2}P(X = x_k) - [E(X)]^2
$$

**Smerodajná odchýlka**, označená ako $\sigma(X)$, je definovaná ako odmocnina z rozptylu

$$
\sigma(X) = \sqrt{D(X)}
$$
:::

> Stredná hodnota predstavuje číslo, **okolo ktorého kolísajú výberové priemery** vypočítané zo série pozorovaných hodnôt náhodnej veličiny. Vypočíta sa ako súčet vynásobenia hodnoty náhodnej veličiny s jej pravdepodobnosťou.
> [color=#0047AB]

### Spojitá náhodná veličina

:::success
Náhodná veličina je **spojitá**, ak jej hodnoty priradené prvom výberového priestoru $\Omega$ tvorí interval na osi reálnych čísel, pričom každý bod tohto intervalu má nenulovú pravdepodobnosť.
:::

>**Spojitou náhodnou veličinou** je teda všetko, čo nadobúda spojité hodnoty. Nadobúda hodnoty z konečného alebo nekonečného intervalu, tzn. môže sa meniť spojite **bez skokov**.
> [color=#0047AB]

> **Príklad**: doba čakania na šalinu, analógový signál
> [color=purple]

:::info
Hustota pravdepodobnosti popisuje správanie náhodnej veličiny. Hustota predstavuje ekvivalent pravdepodobnostnej funkcie diskrétnej náhodnej veličiny, a teda platí

$$
\int_{-\infty}^{\infty} f(x)dx = 1
$$

Pravdepodobnosť, že spojitá náhodná veličina nadobudne hodnoty z intervalu $\langle x_1;x_2 \rangle$ môže byť vypočítaná ako

$$
P(x_1 \leq X \leq x_2) = \int_{x_1}^{x_2} f(t)dt
$$
:::

>Plocha pod krivkou rozdelenia sa rovná jednej, pretože pokrýva všetky hodnoty, ktoré môže náhodná veličina nadobudnúť.
> [color=#0047AB]

:::success
**Distribučná funkcia** spojitej náhodnej veličiny $X$ je nezáporná funkcia

$$
F(x) = \int_{-\infty}^{x} f(t) dt
$$

Distribučnú funkciu $F(x)$ je možné vyjadriť ako **plochu pod krivkou pravdepodobnostného rozdelenia**.

Pravdepodobnosť, že spojitá náhodná veličina nadobudne hodnoty z intervalu $\langle x_1;x_2 \rangle$ môže byť zároveň vyjadrená aj pomocou distribučnej funkcie, a to nasledujúcim spôsobom

$$
P(x_1 \leq X \leq x_2) = F(x_2) - F(x_1)
$$

:::

>Od pravdepodobnosti, že náhodná veličina $X$ nadobudne hodnoty $x_2$ a menšie odčítame pravdepodobnosť, že nadobude hodnoty $x_1$ a menšie. Ostane nám teda plocha medzi bodmi $x_2$ a $x_1$, ktorá značí pravdepodobnosť, že $X$ nadobudne hodnoty v tomto intervale.
> [color=#0047AB]

>**Vyznačenie hodnoty distribučnej funkcie $F(x_i)$:**
>

:::success
K popisu spojitej náhodnej veličiny sa používajú číselné charakteristiky. Najdôležitejšou z nich je **stredná hodnota** (očakávaná hodnota), označovaná ako $E(X)$, ekvivalentne aj $EX$, definovaná ako

$$
E(X) = \int_{-\infty}^{\infty} xf(x)dx
$$

Ďalšou charakteristikou je **rozptyl**, označovaný ako $D(X)$ alebo aj $var(X)$, ktorý je možné vyjadriť ako

$$
D(X) = \int_{-\infty}^{\infty} x^2f(x)dx - [E(X)]^2
$$

K popisu hodnôt rozptýlenia spojitej náhodnej veličiny sa pouźíva častejšie **smerodajná odchýlka**, označená ako $\sigma(X)$. Je definovaná ako

$$
\sigma(X) = \sqrt{D(X)}
$$
:::

>Stredná hodnota u spojitej náhodnej veličiny má rovnaký význam ako pri diskrétnej.
> [color=#0047AB]

## Náhodný výber

:::success
**Náhodný výber** je usporiadaná n-tica náhodných veličín $X_1, \ldots, X_n$, ktoré sú stochasticky **nezávislé** a majú **rovnaké rozdelenie** (ale nemusíme ho konkrétne poznať).

Realizáciou náhodného výberu sú konkrétne hodnoty $x_1, \ldots, x_n$.
:::

:::info
**Štatistika** je ľubovoľná funkcia náhodného výberu.
:::

:::warning
:book: https://mathstat.econ.muni.cz/media/12421/nahodny_vyber_statistika.pdf
:book: https://web.vscht.cz/~zikmundm/astat/poznamky_k_AS_7.pdf
:::

## Parametrické pravdepodobnostné modely NV (rozdelenia)

:::warning
:bar_chart: Pre fajnšmekrov: [Databáza rozdelení pravdepodobnosti](https://sites.google.com/site/probonto/)
:book: Pre menších fajnšmekrov: [Tabuľka vzťahov medzi rozdeleniami](https://www.statlect.com/probability-distributions/)
:::

### Diskrétne rozdelenia

#### Bernoulliho rozdelenie (alternatívne)

:::info
Popisuje udalosti s **dvoma možnými výsledkami** (úspech, neúspech), pričom úspech má pravdepodobnosť $p$, neúspech $1-p$.
:::

> :bulb: $\text{Bernoulli}(p)$ = $\text{Binomial}(1, p)$
> [color=#0047AB]

> **Príklad:** úspešné ukončenie predmetu.
> [color=purple]

:::success
Náhodná veličina $X$ má **Bernoulliho rozdelenie** s parametrom $p \in (0, 1)$ ak je jej pravdepodobnostná funkcia definovaná nasledovne:

$$
p(x) = P(X = x) =
\begin{cases}
1 - p & x = 0 \\
p & x = 1 \\
0 & \text{inak.}
\end{cases}
$$

- $X \sim \text{Bernoulli}(p)$
- $EX = p$
- $\text{var}X = p(1-p)$
:::

> **Pravdepodobnostná funkcia** pre $p=0.65$
>
> 
>
> **Distribučná funkcia** pre $p=0.65$
>
> 

#### Binomické rozdelenie

:::info
Popisuje **počet úspechov** v $n$ opakovaných (medzi sebou nezávislých) Bernoulliho pokusoch, pričom $p$ je pravdepodobnosť úspechu v jednom pokuse.
:::

> **Príklad:** počet študentov, ktorí úspešne ukončia predmet.
> [color=purple]

:::success
Náhodná veličina $X$ má **binomické rozdelenie** s parametrami $n \in \mathbb{N}$ a $p \in (0,1)$ ak je jej pravdepodobnostná funkcia definovaná nasledovne:

$$
p(x) = P(X = x) =
\begin{cases}
{n \choose x} p^x(1-p)^{n-x} \\
0 & \text{inak.}
\end{cases}
$$

- $X \sim \text{Binomial}(n,p)$
- $EX = np$
_(čím vyššia pravdepodobnosť úspechu, tým väčší počet úspešných pokusov)_
- $\text{var}X = np(1-p)$
:::

> **Pravdepodobnostná funkcia:**
>
> 
>
> _Pozn.: graf pripomína pravdepodobnostnú funkciu normálneho rozdelenia, viď napr. aproximácia normálnym rozdelením pomocou centrálnej limitnej vety._
>
> **Distribučná funkcia:**
>
> 

#### Poissonovo rozdelenie

:::info
Popisuje **počet výskytov nezávislej udalosti za fixný** (časový/priestorový/...) **interval**.
:::

> **Príklad:** počet prichádzajúcich hovorov do call centra za hodinu, počet narodených detí v Česku za deň
> [color=purple]

:::success
Náhodná veličina $X$ má **Poissonovo rozdelenie** s parametrom $\lambda > 0$ ak je jej pravdepodobnostná funkcia definovaná nasledovne:

$$
p(x) = P(X = x) =
\begin{cases}
e^{-\lambda\frac{\lambda^x}{x!}} & x = 0, 1, ..., \\
0 & \text{inak.}
\end{cases}
$$

- $X \sim \text{Pois}(\lambda)$
- $EX = \lambda$
- $\text{var}X = \lambda$
- $\lambda$ = očakávaný počet výskytov udalosti za daný interval
:::

> **Pravdepodobnostná funkcia:**
>
> 
>
> **Distribučná funkcia:**
>
> 

#### Geometrické rozdelenie

:::info
Popisuje **počet zlyhaní** v opakovanom Bernoulliho experimente **pred prvým úspechom**.
:::

> **Príklad:** počet zlyhaní než na kocke hodíme šestku, počet prenesených bitov než sa stane prvá chyba (ak prenášame len do prvej chyby)
> [color=purple]

:::success
Náhodná veličina $X$ má **geometrické rozdelenie** s parametrom $p \in (0, 1)$ ak je jej pravdepodobnostná funkcia definovaná nasledovne:

$$
p(x) = P(X = x) =
\begin{cases}
p(1-p)^x & x = 0, 1, \ldots, \\
0 & \text{inak.}
\end{cases}
$$

- $X \sim \text{Geom}(p)$
- $EX = \frac{1-p}{p}$
- $\text{var}X = \frac{1-p}{p^2}$
:::

> Niekedy sa definuje aj ako $p(x) = p(1-p)^{x-1}$ pre $x = 1, 2, \ldots$, podľa toho, či nás zaujíma počet zlyhaní pred úspechom (vyššie) alebo počet pokusov potrebných na dosiahnutie prvého úspechu (tj. s úspechom vrátane).
> [color=green]

> **Pravdepodobnostná funkcia:**
> (vľavo definícia "vrátane", vpravo definícia "počet zlyhaní")
> 
>
> **Distribučná funkcia:**
> (vľavo definícia "vrátane", vpravo definícia "počet zlyhaní")
> 

#### (Diskrétne) rovnomerné rozdelenie

:::info
Rovnaká pravdepodobnosť pre každý jav z množiny $A$.
:::

> **Príklad**: posledná cifra náhodne vybraného telefónneho čísla, počet bodiek na kocke pri jednom hode
> [color=purple]

:::success
Náhodná veličina $X$ má **diskrétne rovnomerné rozdelenie** na konečnej množine $A$ ak je jej pravdepodobnostná funkcia definovaná nasledovne:

$$
p(x) = P(X = x) =
\begin{cases}
\frac{1}{A} & x \in A, \\
0 & \text{inak.}
\end{cases}
$$

- $X \sim \text{Uniform}(A)$
- neexistuje všeobecný vzorec pre $EX$ a ani $\text{var}X$
:::

> **Pravdepodobnostná funkcia:**
>
> 
>
> **Distribučná funkcia:**
>
> 

### Spojité rozdelenia

#### Rovnomerné rozdelenie

> [color=#0047AB]

:::info
Priraďuje všetkým hodnotám náhodnej veličiny **rovnakú pravdepodobnosť**. Používa sa pri generovaní pseudonáhodných čísel.
:::

:::success
Spojitá náhodná veličina X má **rovnomerné rozdelenie** na intervale $(a,b)$, kde parametre $a,b$ sú ľubovoľné reálne čísla, pre ktoré platí, že $a<b$ práve vtedy, ak jej hustota pravdepodobnosti má nasledujúci tvar

$$
f(x) =
\begin{cases}
\frac{1}{b-a}; x \in (a,b), \\
0 ; x \notin (a,b)
\end{cases}
$$

Distribučná funkcia má tvar:

$$
F(x) =
\begin{cases}
0; x < 0, \\
\frac{x-a}{b-a}; a < x < b, \\
1; x \geq b
\end{cases}
$$

- $X \sim \text{R}(a,b)$
- $E(X) = \frac{a+b}{2}$
- $\text{var}(X) = \frac{(b-a)^2}{12}$
:::

>**Funkcia hustoty rozdelenia**:
>
>

> [color=purple]

#### Exponenciálne rozdelenie

:::info
Vyjadruje **čas medzi náhodne sa vyskytujúcimi udalosťami**. Využíva sa napríklad v poistnej matematike pri určení času medzi poistnými udalosťami. Pravdepodobnosť nastania udalosti nezávisí na prečkanej dobe.
:::

:::success
Spojitá náhodná veličina X má **exponenciálne rozdelenie** s parametrom $\lambda > 0$ práve vtedy, ak jej hustota pravdepodobnosti má nasledujúci tvar:

$$
f_x(x) =
\begin{cases}
\lambda e^{-\lambda x}; x > 0, \\
0 ; x \leq 0
\end{cases}
$$

Distribučná funkcia má tvar:

$$
F(x) =
\begin{cases}
1 - e^{-\lambda x}; x > 0, \\
0 ; x \leq 0
\end{cases}
$$

- $X \sim \text{Exp}(\lambda)$
- $E(X) = \frac{1}{\lambda}$
- $\text{var}(X) = \frac{1}{\lambda^2}$
:::

>**Hustota exponenciálneho rozdelenia:**
>

> [color=#0047AB]

> [color=purple]

#### Normálne rozdelenie

:::info
Normálne rozdelenie, niekedy nazývané aj **Gaussovo rozdelenie**, je najčastejšie používané rozdelenie. Má mnoho významných teoretických vlastností a z hľadiska aplikácie býva vhodné na vyjadrenie náhodných veličín, ktoré je možné interpretovať ako aditívny výsledok veľa nezávislých vplyvov (chyba merania, odchýlka rozmeru výrobku od požadovanej hodnoty, atď).
:::

:::success
**Normálne rozdelenie** pravdepodobnosti s parametrami $\mu$ a $\sigma^2$, kde $\sigma%2 > 0$, má hustotu:

$$
f(x) = \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}
$$

- $X \sim \text{N}(\mu, \sigma^2)$
- $E(X) = \mu$
- $\text{var}(X) = \sigma^2$

\
Rozdelenie $\text{N}(0, 1)$ sa označuje ako **normované alebo štandardizované normálne rozdelenie**. Toto rozdelenie má teda hustotu:

$$
f(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}
$$
:::

>**Grafy hustôt normálneho rozdelenia:**
>
>
>
>**Grafy odpovedajúcich distribučných funkcií:**
>
>

:::success
**Transformáciou** náhodnej veličiny $X$ s rozdelením $N(\mu, \sigma^2)$ na náhodnú veličinu

$$
U = \frac{X - \mu}{\sigma}
$$

dostaneme náahodnú veličinu s **normovaným (štandardizovaným) normálnym rozdelením** $\text{N}(0, 1)$ a distribučnou funkciou $F(u)$.

:::

> Zmenšovanie parametru $\mu$ posúva rozdelenie po osi $x$ vľavo, zväčšovanie ho posúva vpravo. Čím väčší je parameter $\sigma^2$, tým viac plochá je krivka (hodnoty sa viac líšia od priemeru). Štandardizáciúou sa od náhodnej veličiny odčíta jej stredná hodnota $\mu$, čím sa krivka posunie na x-ovej osi na bod 0.
> [color=#0047AB]

:::success
Pre hodnoty $F(u)$ distribučnej funkcie normovaného normálneho rozdelenia platí

$$
F(-u) = 1 - F(u)
$$

dostaneme náahodnú veličinu s **normovaným (štandardizovaným) normálnym rozdelením** $\text{N}(0, 1)$.

Pre kvantily normovaného normálneho rozdelenia platí

$$
u_{1-P} = -u_P
$$

kde $0 < P < 1$.

:::

> Tieto vlastnosti plynú zo stredovej symetrie rozloženia. Pre ilustráciu si môžeme za $u$ pri výpočte hodnoty distribučnej funkcie dosadiť číslo 0,5. Po odčítaní hodnoty $F(0,5)$ od 1 dostaneme pravdepodobnosť, ktorá je vďaka stredovej symetrii rovnaká ako $F(-0,5)$
> [color=#0047AB]
>
:::success
Ak má náhodná veličina $X$ normálne rozloženie $N(\mu, \sigma^2)$, jej distribučnú funkciu je možné vyjadriť ako

$$
F(X) = F(\frac{x-\mu}{\sigma})
$$
:::

> [color=#0047AB]

> [color=purple]

#### Chi-kvadrát rozdelenie

:::info
Rozdelenie zvykne byť používané pri určovaní intervalových odhadov neznámych parametrov a pri testovaní hypotéz.
:::

:::success
Rozdelenie **chi kvadrát**, taktiež nazývané aj **Pearsonovo rozdelenie**, s $n$ stupňami voľnosti je spojité rozdelenie pravdepodobnosti. Hustota pravdepodobnosti rozdelenia má tvar

$$
f(x) =
\begin{cases}
0; x \leq 0, \\
\frac{1}{\Gamma(\frac{n}{2})2^{\frac{n}{2}}}e^{-\frac{x}{2}}x^{\frac{n}{2}-1} ; x > 0
\end{cases}
$$

- $X \sim \chi^2(n)$
- $E(X) = n$
- $\text{var}(X) = 2n$

:::

>**Grafy hustôt chi kvadrát rozdelenia:**
>$k$ značí počet stupňov voľnosti
>

> [color=#0047AB]

> [color=purple]

#### Log-normálne rozdelenie

:::info
Logaritmicko-normálne rozdelenie s parametrami $\mu$ a $\sigma$ je spojité rozdele pravdepodobnosti jednorozmernej reálnej náhodnej veličiny $X$ také, že náhodná veličina $ln(X)$ má normálne rozdelenie so strednou hodnotou $\mu$ a smerodajnou odchýlkou $\sigma$.
:::

:::success

Hustota **logaritmicko-normálneho rozdelenia** má tvar

$$
fx(x) = \frac{1}{x\sigma\sqrt{2\pi}} e^{-\frac{(ln x-\mu)^2}{2\sigma^2}}, x > 0
$$

- $X \sim LN(\mu, \sigma)$
- $EX = e^{\mu + \sigma^2/2}$
- $\text{var}X = (e^{\sigma^2} - 1)e^{2\mu + \sigma^2}$

:::

>**Hustoty logaritmicko-normálneho rozdelnia:**
>

> [color=#0047AB]

> [color=purple]

#### Studentovo t-rozdelenie

:::info
Studentovo rozloženie je spojité rozdelenie pravdepodobnosti, ktoré sa najčastejšie používa pri **určovaní intervalových odhadov a pri testovaní štatistických hypotéz**.
:::

:::success
Nech $X$ je náhodná veličina a $n$ je prirodzené číslo. Potom táto náhodná veličina $X$ má **Studentovo rozloženie** (taktiež nazývané aj **t-rozloženie**) s $n$ stupňami voľnosti, pokiaľ jej hustota pravdepodobnosti má nasledovný tvar

$$
f_n(x) = \frac{\Gamma(\frac{n+1}{2})}{\Gamma \frac{n}{2} \sqrt{n\pi}} (1+\frac{x^2}{n})^{-\frac{n+1}{2}}
$$

- $X \sim \text{t}(n)$
- $EX = \mu$
- $\text{var}X = \sigma^2$
:::

> Stupne voľnosti reprezentujú počet nezávislých údajov, na ktorých je založený parametrický odhad.
> [color=#0047AB]

> **Funkcia hustoty Studentovho rozdelenia:**
> ($v$ značí počet stupňov voľnosti)
> 

> [color=#0047AB]

> [color=purple]

## Centrálna limitná veta (CLV, _Central Limit Theorem_)

:::warning
:book: [CLV na portálu matematické biologie](https://portal.matematickabiologie.cz/index.php?pg=aplikovana-analyza-klinickych-a-biologickych-dat--biostatistika-pro-matematickou-biologii--bodove-a-intervalove-odhady--teoreticke-pozadi-intervalovych-odhadu--centralni-limitni-veta)
:movie_camera: [StatQuest: The Central Limit Theorem [YouTube]](https://www.youtube.com/watch?v=YAlJCEDH2uY)

:::

> **Centrální limitní věta** je klíčové matematické tvrzení, které popisuje pravděpodobnostní chování **výběrového průměru pro velké vzorky** a umožňuje tak sestrojení intervalových odhadů, a to nejen pro normálně rozdělené náhodné veličiny.
> [color=#0047AB]

:::success
**_Lindeberg-Lévy CLV_**

Mějme posloupnost $X_1, \ldots, X_n$ nezávislých, stejně rozdělených náhodných veličin (a.k.a. **náhodný výběr**), které mají konečnou střední hodnotu $\mu$ a rozptyl $\sigma^2 > 0$. Pak asymptoticky pro $n \rightarrow \infty$ platí:

$$
(1)\quad\overline{X} = \frac{1}{n}\sum^{n}_{i=1}{X_i} \approx \mathcal{N}(\mu, \frac{\sigma^2}{n}) \\
(2)\quad\sqrt{n}\frac{\overline{X}-\mu}{\sqrt{\sigma^2}} \approx \mathcal{N}(0,1) \\
(3)\quad\frac{\sum^{n}_{i=1}{X_i - n\mu}}{\sqrt{n\sigma^2}} \approx \mathcal{N}(0,1)
$$
:::

> Komentár: bez ohľadu na to, z akého rozdelenia máme náhodné výbery, výberový priemer bude mať (pre dostatočne veľké $n$) asymptoticky normálne rozdelenie s určitými parametrami (viď $(1)$ vyššie). Po vhodnej normalizácii výberového priemeru dostaneme asymptoticky štandardné normálne rozdelenie $\mathcal{N}(0,1)$ (viď $(2)$ a $(3)$ vyššie).
> [color=#0047AB]

> :bulb: Centrální limitní věta funguje dokonce i tehdy, když rozdělení původní náhodné veličiny není spojité, ale **diskrétní**.
> [color=#0047AB]

:::info
**Zjednodušená interpretace CLV**: pokud je rozdělení pravděpodobnosti náhodné veličiny $X$ **normální**, pak je i **rozdělení průměru** pozorovaných hodnot **normální** (a to i pro $n = 1$). Pokud však rozdělení pravděpodobnosti náhodné veličiny $X$ normální není, pak je rozdělení průměru pozorovaných hodnot **přibližně normální**, když **$n$ je dostatečně velké** (matematicky řečeno, pro n jdoucí do nekonečna).
:::
> **Minimální velikost souboru** pro výpočet průměru (Lindeberg-Lévy):
> [color=#0047AB]
> - $n \ge 30$ v případě rozdělení pravděpodobnosti podobných normálnímu;
> - $n \ge 100$ pro rozdělení, která nejsou podobná normálnímu
>
> *(názory na minimálni hodnoty $n$ se liší)*

> Teória a zároveň **princíp použitia CLV** pre výpočet pravdepodobnosti:
> 
> [name=MV013, lecture 4][color=green]

> 
> 
> [name=MV013, lecture 4][color=green]

> **Príklad** výpočtu s použitím CLV
> 
> [name=MV013, lecture 4][color=purple]
> :::info
> :bulb: _Continuity correction_ (oprava na spojitosť) sa používa pri aproximácii diskrétneho rozdelenia spojitým.
>
> Pre diskrétne rozdelenia $P(X \le x) = P(X \lt x + 1)$. Ak platia podmienky Moivre-Laplaceovej CLV, dá sa vyššie uvedené aproximovať pomocou $P(Y \lt x + 0.5)$
> :::
>

## Bodové a intervalové odhady, princíp vieryhodnosti

> Cieľom odhadu je určenie neznámeho parametru náhodnej veličiny $X$ na základe informácie obsiahnutej vo výberovom súbore (realizácií náhodnej veličiny, datasete). Zaujíma nás predovšetkým **hodnota a presnosť odhadu**.
> [color=#0047AB]

:::info
**Nestranný odhad** _(unbiased estimator)_ parametru $\theta$ je odhad, jehož střední hodnota je rovna θ a to pro každou hodnotu, které může tento parametr ze své definice nabývat. Nestrannost odhadu je celkem logickým omezením, které nám říká, že tento odhad má vzhledem ke střední hodnotě nulové vychýlení.

**Nejlepší nestranný odhad** má ze všech nestranných odhadů nejmenší rozptyl (variabilitu).
:::
> **Příklad nestranného odhadu:** výběrový průměr jako odhad střední hodnoty (parametru $\mu$) normálního rozdělení.
> [color=purple]

:::info
**Konzistentný odhad**
:::

### Bodový odhad (_point estimate_)

> Parameter odhadujeme pomocou **jednej hodnoty**, ktorá sa snaží hodnotu parametru **aproximovať**.
> [color=#0047AB]

> 
> [color=green]
> 
> [name=MV011]

### Intervalový odhad (_range estimate_)

> Parameter odhadujeme pomocou **intervalu**, ktorý daný parameter s veľkou pravdepodobnosťou obsahuje. Dĺžka intervalu vypovedá o presnosti odhadu.
> [color=#0047AB]

:::success
**Interval spolehlivosti** (**konfidenční interval**) pro parametr $\theta$ se spolehlivostí $1 - \alpha$, kde $\alpha \in [0,1]$, je dvojice statistik $(T_d(\mathbf{X}), T_h(\mathbf{X}))$ taková, že

$$P(T_d(\mathbf{X}) \leq \theta \leq T_h(\mathbf{X})) = 1 - \alpha$$
:::

> * **Intervalový odhad** je konkrétní realizace intervalu spolehlivosti.
> * Koeficient $\alpha$ nazýváme **hladinou významnosti**.
> * Pro **oboustranný** intervalový odhad platí $P(\theta \leq T_d(\mathbf{X})) = P(\theta \geq T_h(\mathbf{X})) = \frac{\alpha}{2}$
> * Pro **levostranný** (dolní) intervalový odhad platí $P(T_d(\mathbf{X}) \leq \theta) = 1 - \alpha$
> * Pro **pravostranný** (horní) intervalový odhad platí $P(\theta \leq T_h(\mathbf{X})) = 1 - \alpha$
> [color=green]
> 

> #### Tvorba intervalového odhadu
> 1. Zvolíme vhodnou výběrovou charakteristiku $T(\mathbf{X})$ jejíž rozdělení závislé na $\theta$ známe.
> 2. Určíme $\alpha$ a kvantily $t_{\frac{\alpha}{2}}$ a $t_{1-\frac{\alpha}{2}}$ z $T(\mathbf{X})$
> 3. Stanovíme meze pro $\theta$ z podmínky $t_{\frac{\alpha}{2}} \leq T(\mathbf{X}) \leq t_{1 - \frac{\alpha}{2}}$
> 4. Profit!
> [color=#0047AB]

> **Příklad:** intervalový odhad střední hodnoty $\mu$ **normálního rozdělení** s neznámým rozptylem se spolehlivostí $0.95$. Máme vzorek velikosti $n$ s výběrovým průměrem $\bar{X}$ a výběrovým rozptylem $S^2$.
> 1. Zvolíme statistiku $T(\mathbf{X}) = \frac{\overline{X} - \mu}{S}\sqrt{n}$
> 2. Z vlastností Studentova rozdělení víme: $T(\mathbf{X}) \sim t(n-1)$
> 3. Dosadíme:
> $$P(t_{\frac{\alpha}{2}}(n-1) \leq \frac{\bar{X} - \mu}{S} \sqrt{n} \leq t_{1 - \frac{\alpha}{2}}(n-1)) = 0.95$$
> 4. Využijeme $t_{\frac{\alpha}{2}}(n-1) = -t_{1-\frac{\alpha}{2}}(n-1)$, tedy:
> $$P(-t_{1-\frac{\alpha}{2}}(n-1) \leq \frac{\bar{X} - \mu}{S} \sqrt{n} \leq t_{1 - \frac{\alpha}{2}}(n-1)) = 0.95$$
> 5. Vytáhneme vše z prostředku:
> $$P(\bar{X}-\frac{S}{\sqrt{n}}t_{1-\frac{\alpha}{2}}(n-1) \leq \mu \leq \bar{X}+\frac{S}{\sqrt{n}}t_{1-\frac{\alpha}{2}}(n-1)) = 0.95$$
> 6. Vyčíslíme.
> [color=purple]

### Princíp vieryhodnosti (_likelihood principle_)

#### Maximum likelihood estimate

> Log-likelihood funkcia a likelihood funkcia majú maximum v rovnakom bode, s log-likelihoodom sa lepšie pracuje.
> [color=#0047AB]

Alternatívne metódy odhadovania parametrov:
- _method of moments_
- _ordinary least-squares method_

Obe metódy sú neparametrické -> MLE využíva informáciu o rozdelení pravdepodobnosti a je _most efficient estimator_.
Nevýhody: zložitejší výpočet, treba riešiť predpoklady o rozdelení (v prípade potreby sa dá použiť CLV).

## Štatistická inferencia -- testovanie hypotéz

:::warning
:book: [Príklady voľby štatistík pri rôznych testoch](https://k101.unob.cz/~neubauer/pdf/testy_hypotez2.pdf)
:::

> Cieľom testovania hypotéz je overiť, či dáta **nepopierajú predpoklad** (hypotézu).
> [color=#0047AB]

Nulová hypotéza $H_0$
Alternatívna hypotéza $H_1$
> Alternatívna hypotéza je to, čo nás v skutočnosti zaujíma.
> [color=#0047AB]

$p$-value je

#### Chyby v testovaní hypotéz

:::info
Chyba 1. typu nastane, keď **zamietneme** $H_0$ aj napriek tomu, že v skutočnosti **platí**.

Chyba 2. typu nastane, keď **nezamietneme** $H_0$ aj napriek tomu, že v skutočnosti **neplatí**.
:::

| | $H_0$ platí | $H_1$ platí |
| ------------------ | --------------------- | --------------------- |
| zamietame $H_0$ | :x: chyba 1. typu | :heavy_check_mark: OK |
| nezamietame $H_0$ | :heavy_check_mark: OK | :x: chyba 2. typu |

> 
[color=green]

### Parametrické testy
#### ANOVA

> **ANOVA** (**AN**alysis **O**f **VA**riance) je **parametrickým** testem testujícím zda na hodnotu náhodné veličiny má statisticky významný vliv hodnota některého znaku, který se u náhodné veličiny dá pozorovat.
> [color=#0047AB]

### Neparametrické testy

> Motivací pro neparametrické testy je fakt, že pro parametrické testy je třeba splnit podmínky (normalita, homogenita, …). Nevýhodou neparametrických je však slabší test (tedy zamítnutí $H_0$ je méně pravděpodobné).
> [color=#0047AB]

## Lineárny regresný model