# Binary adders
contributed by < [Eric Lin](https://github.com/ericlinsechs) >

## Half adder

### Overview
A half adder is a fundamental digital circuit that computes the sum `S` and carry `C` outputs based on two input bits.

The carry signal represents an overflow into the next digit of a multi-digit addition.

The formula for the sum and carry is as follows:
$S = A \oplus B$
$C = A \cdot B$

### True Table

| A | B | C | S |
| --- | --- | --- | --- |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |

### digital logic circuits


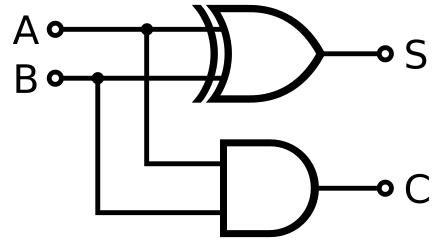
### Limitation
It is not designed to handle the complexities of multi-bit addition, lacking the ability to accommodate the expansion required for more significant binary numbers.

### Code implementation

#include <stdio.h>

int half_adder(int x, int y) 
{
    return x ^ y + (( x & y ) << 1);
}

int main() 
{
    int x, y, ans;

    printf("Enter x (0 or 1): ");
    scanf("%d", &x);

    printf("Enter y (0 or 1): ");
    scanf("%d", &y);

    ans = half_adder(x, y);

    printf("ans: %d\n", ans);

    return 0;
}

## Full adder

### Overview
A full adder is designed to perform the addition of three binary digits: two inputs ($A$ and $B$) and a carry input from the previous stage $C~in~$. It produces two outputs: a sum $S$ and a carry $C~out~$.

The sum $S$ is the result of adding the three inputs and is given by the XOR (exclusive OR) operation:

$S = A \oplus B \oplus C~in~$

The carry $C~out~$:

$C~out~ = A \cdot B + C~in~ (A \oplus B)$

### True Table

| A | B | C~in~ | S | C~out~ |
| --- | --- | ----- | --- | ------ |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |

### digital logic circuits


### Cascading Full Adders
Full adders can be connected in series to create a **ripple-carry adder**, allowing the addition of multi-bit binary numbers. The carry output $C~out~$ from one full adder becomes the carry input $C~in~$ for the next, enabling the propagation of carry through multiple stages.

### Code implementation

#include <stdio.h>

typedef char bit;

void full_adder(bit a, bit b, bit cin, bit *sum, bit *cout) 
{
    *sum = a ^ b ^ cin;
    *cout = a & b | cin & (a ^ b);
}

int main() 
{
    int x, y;

    // Input integer numbers x and y
    printf("Enter integer x: ");
    scanf("%d", &x);

    printf("Enter integer y: ");
    scanf("%d", &y);

    int sum = 0, multiplier = 1; // Used to process each bit position
    bit carry = 0;
    
    while (x > 0 || y > 0 || carry > 0) {
        bit bit_x = x & 0x1;
        bit bit_y = y & 0x1;
        bit bit_sum = 0;

        // Perform addition using full adder
        full_adder(bit_x, bit_y, carry, &bit_sum, &carry);

        // Update the sum using the current bit position
        sum += (bit_sum * multiplier);

        // Move to the next bit position
        x >>= 1;
        y >>= 1;
        multiplier <<= 1;
    }

    // Output the result
    printf("Sum: %d\n", sum);

    return 0;
}

> Reading: [How to simulate a 4-bit binary adder in C](https://stackoverflow.com/questions/14695051/how-to-simulate-a-4-bit-binary-adder-in-c)