# 記事1本目 固有値、固有ベクトルの応用例(三部作)
## はじめに
この記事は[古川研究室 Workout_calendar](https://qiita.com/flab5420/private/aee38a24be700d146817) 13日目の記事です。
本記事は古川研究室の学生が学習の一環として書いたものです。内容が曖昧であったり表現が多少異なったりする場合があります。
機械学習をやりたい！というエネルギッシュな初心者(私)が必ずつまずく壁が固有値だと思うんです。
固有値は高校数学で意味わからない成りに計算させられるので、「あ、なんか行列に備わってる大事な値なんだなー」くらいの認識はあると思います。
しかし具体的にどう使うの？とか何が便利なの？とか数学で抱えがちな疑問を残したまま、記憶の彼方に置き去りにされてしまう人も多いのではないでしょうか(私)。
そして機械学習やるぞ！となったときに固有値を理解する必要に迫られ、あの時ちゃんとやってりゃ良かった...と後悔するのです(私)。
本記事の全体としての目的は、固有値がどういうものかを理解しつつ、二次形式(2本目の記事)と主成分分析(3本目の記事)という比較的簡単な応用例を実装することで、固有値がどう便利なのか、固有値は機械学習でどう使われているのかを知ろうというものです。
## 固有値ってなんだ！？！？！？！？
三部作の最初となるこの記事では、固有値とは何かについて説明していきます。固有値に対するイメージをつかむなら[この記事](https://qiita.com/kenmatsu4/items/2a8573e3c878fc2da306)が素晴らしくピッタリだと思います。
記事を貼り付けるだけなのも情けないのでこちらでも概要だけ説明すると

- 固有値は線形変換後の各座標の倍率
- 固有ベクトルは線形変換後も向きが変わらないベクトル

です。どういうことか直感的に理解するために次の線形変換を行ってみましょう。

\begin{equation}
\begin{pmatrix}
x^{t=2} \\
y^{t=2}
\end{pmatrix}=
\begin{pmatrix}
4 & -2 \\
1 & 1
\end{pmatrix}
\begin{pmatrix}
x^{t=1} \\
y^{t=1}
\end{pmatrix}
\end{equation}

今回は初期値($x^{t=1}$,$y^{t=1}$)=(2,3)とします。また、今後の文章の簡単化のため、右辺の2行2列の正方行列を行列$A$とします。

import numpy as np
import matplotlib.pyplot as plt
plt.figure()
A =np.array([[4,-2],[1,1]])
print(A)
x=np.array([2,3])
x=np.reshape(x,(2,1))
y = np.dot(A,x)
X = 0,0
Y = 0,0
U=[y[0],x[0]]
V=[y[1],x[1]]
colors = [2,1]
plt.quiver(X,Y,U,V,colors,angles='xy',scale_units='xy',scale=1)

plt.xlim([0,5])
plt.ylim([0,5])
plt.grid()
plt.draw()
plt.show()

実行結果

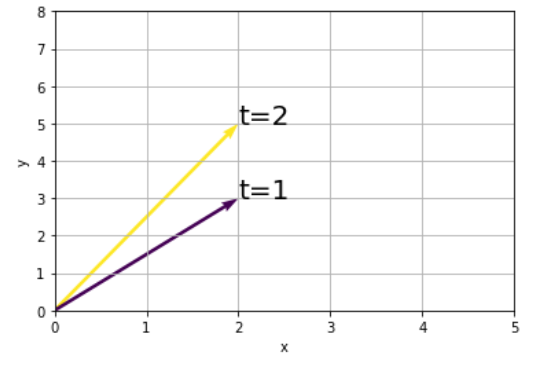
実行結果を見ると、ベクトル(2,3)が、行列$A$によって変形され、ベクトル(2,5)となっていることがわかりますね。
このような「ベクトルを行列によって変換する作業」を線形変換といいます。では同じ行列$A$を用いて別のベクトルを線形変換してみます。

\begin{equation}
\begin{pmatrix}
x^{t=2} \\
y^{t=2}
\end{pmatrix}=
\begin{pmatrix}
4 & -2 \\
1 & 1
\end{pmatrix}
\begin{pmatrix}
1 \\
1
\end{pmatrix}
\end{equation}

import numpy as np
import matplotlib.pyplot as plt
plt.figure()
#plt1.figure
A =np.array([[4,-2],[1,1]])
print(A)
x=np.array([1,1])
x=np.reshape(x,(2,1))
y = np.dot(A,x)
print(y)
X = 0,0
Y = 0,0

colors = [2,1]
plt.quiver(X,Y,x[0],x[1],colors[0],angles='xy',scale_units='xy',scale=1)
plt.quiver(X,Y,y[0],y[1],colors[1],angles='xy',scale_units='xy',scale=1)

plt.xlim([0,5])
plt.ylim([0,5])
plt.grid()
plt.draw()
plt.show()


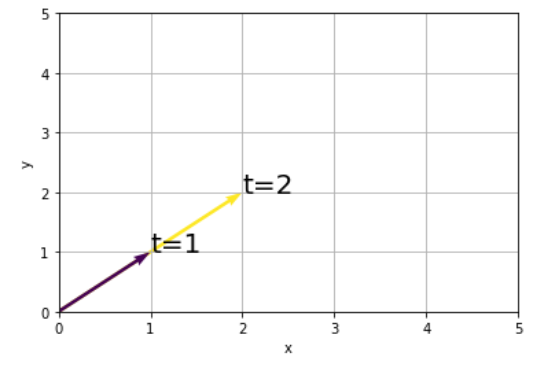
実行結果がこちらです。先ほどとは違って線形変換後もベクトルは同じ方向を向いていますね。
このような、「線形変換後も向きが変わらずに、スカラー倍されるだけのベクトル」を固有ベクトルと呼びます。固有ベクトル以外のベクトルを線形変換すると向きも大きさも変わってしまいますが、固有ベクトルだけは大きさが変化するのみなんですね。
順序が入れ替わっている気がしなくもなくもないですが、今回用いた行列$A$について固有値、固有ベクトルを導出してみます。

まずは固有値を固有方程式から算出します。

\begin{equation}
|A-\lambda I| =
\begin{vmatrix}
4-\lambda & -2 \\
1 & 1-\lambda
\end{vmatrix}
=(4-\lambda)(1-\lambda)+2
=\lambda ^2-5\lambda+6
=(\lambda-3)(\lambda-2)
\end{equation}

\begin{equation}
\lambda _1=3,\lambda _2=2
\end{equation}

続いて各固有値に対応した固有ベクトル$\mathbf{p}_1$,$\mathbf{p}_2$を求めます。
まずは$\lambda_1=3$に対応した固有ベクトル$\mathbf{p}_1$を求めます。

\begin{equation}
\begin{pmatrix}
4 & -2 \\
1 & 1
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
=3
\begin{pmatrix}
x \\
y
\end{pmatrix}
\end{equation}

\begin{equation}
4x-2y=3x\\
x=2y\\
\mathbf{p}_1=
\begin{pmatrix}
2 \\
1
\end{pmatrix}
\end{equation}

同様に$\lambda_2=2$に対応した固有ベクトル$\mathbf{p}_2$を求めます。

\begin{equation}
\begin{pmatrix}
4 & -2 \\
1 & 1
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
=2
\begin{pmatrix}
x \\
y
\end{pmatrix}
\end{equation}

\begin{equation}
4x-2y=2x\\
2x=2y\\
\mathbf{p}_2=
\begin{pmatrix}
1 \\
1
\end{pmatrix}
\end{equation}
この計算から、固有値が2,3であること、固有値2に対応する固有ベクトルは(1,1),固有値3に対応する固有ベクトルは(2,1)であることがわかりました。

先ほど線形変換したベクトルは(1,1)で返還後は(2,2)でした。つまり、**固有ベクトルを線形変換すると固有値倍される**のです。
それを改めて確かめるために今度は初期値を(2,1)として試してみましょう。

import numpy as np
import matplotlib.pyplot as plt
plt.figure()
#plt1.figure
A =np.array([[4,-2],[1,1]])
print(A)
x=np.array([2,1])
x=np.reshape(x,(2,1))
y = np.dot(A,x)
print(y)
X = 0,0
Y = 0,0

colors = [2,1]
plt.quiver(X,Y,x[0],x[1],colors[0],angles='xy',scale_units='xy',scale=1)
plt.quiver(X,Y,y[0],y[1],colors[1],angles='xy',scale_units='xy',scale=1)

plt.xlim([0,8])
plt.ylim([0,8])
plt.grid()
plt.draw()
plt.show()


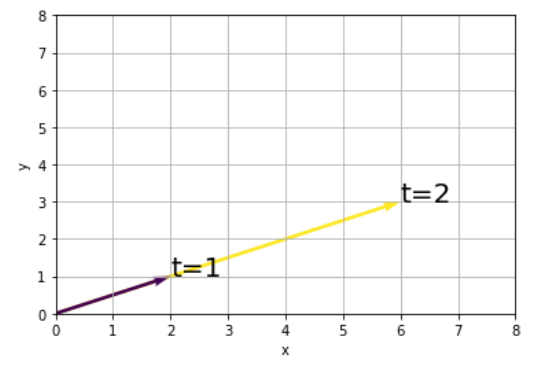
実行結果から、固有ベクトル(2,1)が固有値倍（3倍）されて現れていることがわかりました。
この結果を式で表現すると以下のようになります。
\begin{equation}
\begin{pmatrix}
4 & -2 \\
1 & 1
\end{pmatrix}
\begin{pmatrix}
2 \\
1
\end{pmatrix}
=\begin{pmatrix}
6 \\
3
\end{pmatrix}
\end{equation}
\begin{equation}
A\mathbf{p}_2=\lambda \mathbf{p}_2
\end{equation}

このような$A\mathbf{x}=\lambda \mathbf{x}$となるような固有値$\lambda$,固有ベクトル$\mathbf{x}$を求める問題を**固有値問題**と呼びます。固有値問題という単語は機械学習でもしばしば用いられるので覚えておいて損はありません。
また、固有値に対する固有ベクトルは1つではありません。先ほどの例で示すとベクトル$(2,1)$をスカラー倍して得られるベクトル全てが固有ベクトルとなります。例えば$-1$倍した$(-2,-1)$とか、$2.5$倍した$(5,2.5)$とかも固有ベクトルとなります。
## まとめ
本記事では固有値、固有ベクトルの性質について記述しました。
しかしこの記事を読んだ皆さんの中に
「んなるほど、確かに固有ベクトルは線形変換しても変わらない向きを表していて、固有値はその倍率だね。でも具体的にどこで使うんだいマイケル」
とお考えの方もいらっしゃると思います。
そんなあなたと私のために二本目の記事から固有値の応用例を示していきたいと思います。
# 記事二本目：二次形式への応用
## はじめに
この記事は[古川研究室 Workout_calendar](https://qiita.com/flab5420/private/aee38a24be700d146817) XX日目の記事です。
本記事は古川研究室の学生が学習の一環として書いたものです。内容が曖昧であったり表現が多少異なったりする場合があります。

前回の記事(リンクを貼る予定)では固有値、固有ベクトルとは一体どんなものなのかについて簡単な線形変換から以下の性質を持つものであると理解しました。
- 固有値は線形変換後の各座標の倍率
- 固有ベクトルは線形変換後も向きが変わらないベクトル

しかし固有値、固有ベクトルが具体的にどう使われているか、どう便利なのかについては前回の記事で言及していませんでした。
そこで今回は固有値、固有ベクトルの数学的な応用例の一つである二次形式を紹介します。
## 二次形式への応用
固有値、固有ベクトルの大事さを体感するために、二次形式という数学的な応用例を試してみましょう。

次のような多項式があるとします(a,b,cは定数)。

\begin{equation}
ax^2 + 2bxy + cy^2 = 0 \tag{1}
\end{equation}

このような式を2変数の2次形式と呼びます。$x^2$も$xy$も$y^2$も全部次数は2ですから、2次形式なんですね。
二次形式は大きく二つに分類されます。「ずっと0以上またはずっと0以下を取るもの」と「正と負両方の値をとるもの」です。また、常に0以上の値を取るものを正値定符号、常に0以下の値を取るものを負定値符号といいます。
問題なのは与えられた二次形式をパッと見たところで、それが正定値符号なのか、負定値符号なのか、はたまたそのどちらでもなく正と負を両方取るのかが分からないんですね。これは悔しい。何とかして求めたいところです。
まあごり押しで調べることもできるっちゃできます。以下にその方法を示します。
例として、以下のような二次形式が与えられたとします。

\begin{equation}
3x^2 + 4xy + 3y^2 = 0
\end{equation}

この二次形式が正値定符号、負定値符号であるかは式変形をすることで分かります。

\begin{equation}
\frac{1}{2}(x-y)^2 +\frac{5}{2}(x+y)^2 = 0
\end{equation}

上式から、この関数が取りうる値は全て正の値であることがわかるので、この二次形式は正値定符号であることがわかりました。

しかしこのように式変形が毎回うまいこと行くとは限りません。ですが行列を使うことで、与えられた二次形式が正値定符号か、負定値符号であるか、そのどちらでもないかが容易に判別できます。
ここから先は数式で追っていきましょう。まず、(1)で示した二次形式の式を行列で以下のように書き換えます。

\begin{equation}
ax^2+2bxy+cy^2 =
\begin{pmatrix}
x \\
y
\end{pmatrix}
\cdot
\begin{pmatrix}
a & b \\
b & c
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
\tag{2}
\end{equation}

この式にある(x,y)を固有ベクトル$\mathbf{e}_1$,$\mathbf{e}_2$を用いて線形変換します。

\begin{equation}
\begin{pmatrix}
x \\
y
\end{pmatrix} =
\begin{pmatrix}
\mathbf{e}_1 &\mathbf{e}_2
\end{pmatrix}
\begin{pmatrix}
x' \\
y'
\end{pmatrix}
\end{equation}
これを(2)に代入すると次のようになります。

\begin{equation}
ax^2+2bxy+cy^2 =
\begin{pmatrix}
\mathbf{e}_1 &\mathbf{e}_2
\end{pmatrix}
\begin{pmatrix}
x' \\
y'
\end{pmatrix}
\cdot
\begin{pmatrix}
a & b \\
b & c
\end{pmatrix}
\begin{pmatrix}
\mathbf{e}_1 &\mathbf{e}_2
\end{pmatrix}
\begin{pmatrix}
x' \\
y'
\end{pmatrix}
\tag{3}
\end{equation}
行列$A$=$\begin{pmatrix}
a & b \\
b & c
\end{pmatrix}$の固有ベクトル$\mathbf{e}_1$,$\mathbf{e}_2$は行列$A$によって線形変換されても固有値倍されるだけなので以下のように変形できます。

\begin{equation}
\begin{pmatrix}
a & b \\
b & c
\end{pmatrix}
\begin{pmatrix}
\mathbf{e}_1 &\mathbf{e}_2
\end{pmatrix}=
\begin{pmatrix}
\lambda_1 \mathbf{e}_1 &\lambda_2 \mathbf{e}_2
\end{pmatrix}=
\begin{pmatrix}
\mathbf{e}_1 &\mathbf{e}_2
\end{pmatrix}
\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2
\end{pmatrix}
\tag{4}
\end{equation}

変形した式(4)を(3)に代入します。

\begin{equation}
ax^2+2bxy+cy^2 =
\begin{pmatrix}
\mathbf{e}_1 &\mathbf{e}_2
\end{pmatrix}
\begin{pmatrix}
x' \\
y'
\end{pmatrix}
\cdot
\begin{pmatrix}
\mathbf{e}_1 &\mathbf{e}_2
\end{pmatrix}
\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2
\end{pmatrix}
\begin{pmatrix}
x' \\
y'
\end{pmatrix}
\end{equation}
さらに転置と内積の公式$A\mathbf{x}\cdot \mathbf{y}=\mathbf{x}\cdot A^T \mathbf{y}$を用います。
またここで公式の変数である行列$A$,ベクトル$\mathbf{x,y}$はそれぞれ
$A=\begin{pmatrix}
\mathbf{e}_1 &\mathbf{e}_2
\end{pmatrix}$
$\mathbf{x}=\begin{pmatrix}
x' \\
y'
\end{pmatrix}$
$\mathbf{y}=\begin{pmatrix}
\mathbf{e}_1 &\mathbf{e}_2
\end{pmatrix}
\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2
\end{pmatrix}
\begin{pmatrix}
x' \\
y'
\end{pmatrix}$
です。この公式を用いることで式は以下のように変形できます。

\begin{equation}
ax^2+2bxy+cy^2 =
\begin{pmatrix}
x' \\
y'
\end{pmatrix}
\cdot
\begin{pmatrix}
\mathbf{e}_1 \\
\mathbf{e}_2
\end{pmatrix}
\begin{pmatrix}
\mathbf{e}_1 &\mathbf{e}_2
\end{pmatrix}
\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2
\end{pmatrix}
\begin{pmatrix}
x' \\
y'
\end{pmatrix}
\end{equation}
固有ベクトル$\mathbf{e}_1$,$\mathbf{e}_2$はそれぞれ直交ベクトルなので

\begin{equation}
ax^2+2bxy+cy^2 =
\begin{pmatrix}
x' \\
y'
\end{pmatrix}
\cdot
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}
\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2
\end{pmatrix}
\begin{pmatrix}
x' \\
y'
\end{pmatrix}
=\lambda_1 x'^2 + \lambda_2 y'^2
\end{equation}
と変形できます。これにより、二次形式をその表現行列の固有値で表現することができました。
この式は固有値が全て正だと正値定符号、全て負だと負定値符号、正と負が混ざったときはそのどちらでもないことを示しています。
つまり、二次形式の表現行列の固有値がわかれば、どのような極値を取るのかがわかるということです。
実際の例を見てみましょう
与えられた二次形式の式が、先ほどと同じ$3x^2-4xy+3y^2$だとします。この式を(2)の形に書き換えると、

\begin{equation}
3x^2-4xy+3y^2 =
\begin{pmatrix}
x \\
y
\end{pmatrix}
\cdot
\begin{pmatrix}
3 & -2 \\
-2 & 3
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
\end{equation}

となります。
表現行列Aの固有方程式から固有値を求めると

\begin{equation}
|A-\lambda I| =
\begin{vmatrix}
3-\lambda & -2 \\
-2 & 3-\lambda
\end{vmatrix}
=(3-\lambda)^2-4
=\lambda ^2-6\lambda+5
=(\lambda-1)(\lambda-5)
\end{equation}
となり固有値は1,5となり両方正なので正値定符号であることがわかりました。
実際にそうなのかグラフにしてみてみましょう。

%matplotlib nbagg
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
a=3
b=-2
c=3
x = np.arange(-3, 3, 0.01)
y = np.arange(-3, 3, 0.01)
X, Y = np.meshgrid(x, y)
A=[[a,b],
   [b,c]]
w,v=np.linalg.eig(A)
print('固有値1:%f' % w[0])
print('固有値2:%f' % w[1])
if(w[0]>0 and w[1]>0):
    print('正値定符号')
if(w[0]<0 and w[1]<0):
    print('負値定符号')
if((w[0]>0 and w[1]<0) or (w[0]<0 and w[1]>0)):
    print('どちらでもない')
Z =a*X**2+2*b*X*Y+c*Y**2

fig = plt.figure()
ax = Axes3D(fig)
ax.plot_wireframe(X,Y,Z)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()


実行結果から、この関数は正の値しか取っていないことがわかりました。

おまけとして負定値符号となるパターンと、正と負どちらの値もとるパターンも示したいと思います。
二次形式$-3x^2+4xy-3y^2$の場合
二次形式$3x^2-3y^2$の場合

## まとめ
今回の記事では数学的な応用例である二次形式について記述しました。
パッと見どんな値を取るかわからない二次形式という関数が、固有値、固有ベクトルのおかげでざっくりと、正定値符号であるか負定値符号であるか、そのどちらでもないかが判別できました。
次回はいよいよ最終章となる3本目ですが、1本目の記事で軽く触れた固有値問題の簡単な例である主成分分析について書きたいと思います。

参考文献:ゼロから学ぶ線形代数、機械学習のエッセンス
# 記事3本目：固有値、固有ベクトルの応用例　主成分分析
## はじめに
この記事は[古川研究室 Workout_calendar](https://qiita.com/flab5420/private/aee38a24be700d146817) XX日目の記事です。
本記事は古川研究室の学生が学習の一環として書いたものです。内容が曖昧であったり表現が多少異なったりする場合があります。

ついに「固有値、固有ベクトルってなんだシリーズ」の3本目です。
1本目の記事では｢固有値、固有ベクトルの性質」について
2本目の記事では数学的な応用例として「二次形式」について記述しました

この記事では1本目の記事で軽く触れた固有値問題の例として、機械学習で用いられる次元削減法の1つである主成分分析について記していこうと思います。
## 主成分分析

主成分分析は、次元削減の手法の一つで多次元データを可視化する際などに使われます。
主成分分析で鍵となるのは以下に示す共分散行列です。

\begin{equation}
S = \frac{1}{N}\sum_{n=1}^N(\mathbf{x}_n-\mathbf{\bar x})(\mathbf{x}_n-\mathbf{\bar x})^T
\end{equation}

式中の$\mathbf{x}_n$はD次元の各データ、$\mathbf{\bar x}$は全データの平均を示しています。
D次元データ$\mathbf{x}_n$を1次元空間に射影することを考えます。
また、主成分分析では、射影後のデータの分散がなるべく大きくなるように次元を削減します。
その方がデータの情報が多く残っていると判断しているわけですね。
データを射影するためにD次元のベクトルである$\mathbf{u}$を導入し、$\mathbf{u}$と$\mathbf{x}_n$の行列積を取ります。また、$\mathbf{u}$を単位ベクトルと仮定します。つまり$\mathbf{u}^T\mathbf{u}=1$です。
射影後のデータの分散は
$$
\frac{1}{N}\sum_{n=1}^N\{\mathbf{u}^T\mathbf{x}_n-\mathbf{u}\mathbf{\bar x}\}^2
$$

となります。さらに式を展開していくと
$$
\frac{1}{N}\sum_{n=1}^N(\mathbf{\mathbf{u}^T\mathbf{x}_n-u\mathbf{\bar x})(\mathbf{u}^T\mathbf{x}_n-\mathbf{u}\mathbf{\bar x})}^T
$$

$$
\frac{1}{N}\sum_{n=1}^N\{(\mathbf{u}^T\mathbf{x}_n)(\mathbf{u}^T\mathbf{x}_n)^T-(\mathbf{u}^T\mathbf{x}_n)(\mathbf{u}^T\mathbf{\bar x})^T-(\mathbf{u}^T\mathbf{\bar x})(\mathbf{u}^T\mathbf{x}_n)^T+(\mathbf{u}^T\mathbf{\bar x})(\mathbf{u}^T\mathbf{\bar x})^T\}
$$

$\mathbf{(A^TB)^T=B^TA}$を各項に当てはめて整理すると

$$
\frac{1}{N}\sum_{n=1}^N(\mathbf{u}^T\mathbf{x}_n^2\mathbf{u}-2\mathbf{u}^T\mathbf{\bar x} \mathbf{x}_n\mathbf{u}+\mathbf{u}^T\mathbf{\bar x}^2\mathbf{u})
$$

$\mathbf{u^T,u}$を括りだして

$$
\frac{1}{N}\sum_{n=1}^N\mathbf{u}^T(\mathbf{x}_n^2-2\mathbf{\bar x}_n \mathbf{x}_n+ \mathbf{\bar x}_n^2)\mathbf{u}\\
=\mathbf{u^T}\left \{\frac{1}{N}\sum_{n=1}^N{(\mathbf{x}_n-\mathbf{\bar x})(\mathbf{x}_n-\mathbf{\bar x})}^T\right \}\mathbf{u}
=\mathbf{u}^T\mathbf{Su}
$$

となります。こうして得られた分散$\mathbf{u}^T\mathbf{Su}$を最大化します。$\mathbf{S}$はデータによって定まる共分散行列なので$\mathbf{u}$に対して最大化します。

$\mathbf{u}$を最大化しようとすると「∞にすれば最大じゃんアハハ」と抜かす不届き者が後を絶たないので、制約項を追加します。

$$
\mathbf{u}^TS\mathbf{u}+\lambda (1-\mathbf{u}^T\mathbf{u})
$$

$\lambda$は係数(ラグランジュ乗数）です。この式を$\mathbf{u}$について偏微分して、0となる場所を探します。

$$
S\mathbf{u}-\lambda \mathbf{u}=0\\
S\mathbf{u}=\lambda \mathbf{u}
$$

なんとこの形はこの記事のいっちばん上で記した固有値問題の式$A\mathbf{x}=\lambda \mathbf{x}$と一致しています。つまり$\lambda$は固有値となるわけです。おおんすごいん

$S\mathbf{u}=\lambda \mathbf{u}$ に左から$\mathbf{u}^T$をかけると

$$
\mathbf{u}^TS\mathbf{u}=\lambda \mathbf{u}^T\mathbf{u}
$$

$\mathbf{u}^T\mathbf{u}=1$なので

$$
\mathbf{u}^TS\mathbf{u}=\lambda
$$

となり、分散が最大となるには、共分散行列の固有値から一番大きいものを選び、それに対応する固有ベクトルで射影すればよいということがわかりました。また、2次元、3次元へと射影するためには共分散行列の固有値の大きいものから順にそれに対応する固有ベクトルを選んでいけば良いです。固有値問題すげえ。

例えばデータが4次元の場合だと固有値は4つ出てきます。2次元に可視化するためには固有値が大きい順から二つを主成分とし、その固有値に対応した固有ベクトルによってデータを射影するのです。

実際に体感するために、具体的な実装例を以下に載せます。

print(__doc__)

#PCA：主成分分析
# Code source: Gaël Varoquaux
# License: BSD 3 clause

import numpy as np#numpyをインストール
import matplotlib.pyplot as plt#グラフを書くやつ
from mpl_toolkits.mplot3d import Axes3D#3次元plotを行うためのツール
from sklearn.preprocessing import Normalizer
from sklearn.preprocessing import StandardScaler
from sklearn import decomposition#PCAのライブラリ
from sklearn import datasets#datasetsを取ってくる

n_component=2
np.set_printoptions(suppress=True)
#centers = [[1, 1], [-1, -1], [1, -1]]#3次元配列を作ってる
#print(centers)
fig = plt.figure(2, figsize=(14, 6))
iris = datasets.load_iris()
X = iris.data
y = iris.target
for i in range(4):#各データの平均を元のデータから引いている
    mean = np.mean(X[:,i])
    X[:,i]=(X[:,i]-mean)
X_cov=np.dot(X.T,X)#共分散行列を生成
w,v=np.linalg.eig(X_cov)#共分散行列の固有値、固有ベクトルを算出(固有値は既に大きさ順に並べられている)
for i in range(n_component):#固有値の大きい順に固有ベクトルを取り出す
    Xpc[i]=v[:,i]
Xpc=np.array(Xpc)
Xafter=np.dot(X,Xpc.T)#取り出した固有ベクトルでデータを線形写像する


pca = decomposition.PCA(n_components=2)
pca.fit(X)
Xlib = pca.transform(X)    


ax1 = fig.add_subplot(121)
for label in np.unique(y):
    ax1.scatter(Xlib[y == label, 0],
                Xlib[y == label, 1])
ax1.set_title('library pca')
ax1.set_xlabel("X_axis")
ax1.set_ylabel("Y_axis")
ax2 = fig.add_subplot(122)
for label in np.unique(y):
    ax2.scatter(Xafter[y == label, 0],
                Xafter[y == label, 1])
ax2.set_title('original pca')
ax2.set_xlabel("X_axis")
ax2.set_ylabel("Y_axis")
plt.show()

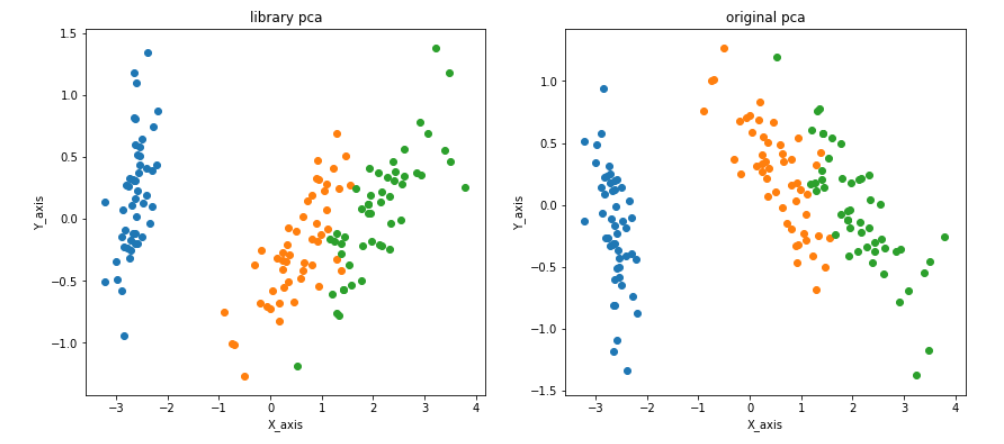
今回はScikit-learnに公開されている[Irisデータセット](https://scikit-learn.org/stable/auto_examples/datasets/plot_iris_dataset.html)という4次元のデータを2次元まで次元削減して可視化しています。
左はscikit-learnで公開されている主成分分析用のライブラリを使った結果、右は数式を実際に再現して主成分分析をした結果を示しています。
右と左で結果が違ってしまっているのは、scikit-learnのライブラリの仕様によるものです。普通固有ベクトルは一意に定まらない（向きが変わる）のですが、scikit-learnでは第1主成分とした固有ベクトルの第1要素が正となるように固有ベクトルを定めているため、結果が反転したりします。
Irisデータセットはアヤメの品種のデータセットです。セトナ、バーシクル、 バージニカという3種類のアヤメのがく片長,がく片幅,花びら長,花びら幅から構成されています。
Irisデータセットをそのまま図示しようとしても各アヤメのデータは4つあるため、2次元や3次元には図示できません。
そこで次元削減を行うのですが、出来るだけ情報を残して次元を落としたいものです。
主成分分析をした結果を見てみると、セトナ、バーシクル、 バージニカの3種類のデータが綺麗に分けられているように見えます。
これが分散の大きい軸を選ぶ利点です。分散の大きい軸を選ぶことで、データの情報を残したまま次元削減しているのです。
そしてそれを可能にしているのが固有値、固有ベクトルという要素なのです。

## まとめ
本記事では固有値問題の一例として主成分分析を実装しました。
それにより、固有値、固有ベクトルが機械学習においても大事な要素であることがわかりました。

3本の記事に渡って固有値、固有ベクトルについて記述しましたが、3本通して読むことで固有値、固有ベクトルとは何か、どのように使われているのかを理解していただければ幸いです。

参考文献:ゼロから学ぶ線形代数、機械学習のエッセンス、パターン認識と機械学習(下巻)