CKB Fee Bumping Mechanism Proposal

As transaction volume continues to increase, so does the demand for block space, which is limited by both transaction serialized size and consumed cycles in CKB.

The user pays a fee as the bidding to the block space. Setting the fee too low may cause the transaction delayed or never confirmed.

Which makes the matters worse, it seems unlikely that the user will always set a proper fee. There are mainly two reasons. First, The fee estimate algorithm could not predict the future fee surge caused by sudden congestion. The second, in applications such as lighting network, the transaction was created long before it is revealed.

The user has to fix the fee issue via fee bumping. This article is a proposal for the fee bumping mechanism for CKB.

How Miners Prioritize Transactions

The miners select transactions to fill the limited block space which gives the highest fee. Because there are two different limits, serialized size and consumed cycles, the selection algorithm is a multi-dimensional knapsack problem.

Virtual Bytes

Introducing the transaction virtual bytes converts the multi-dimensional knapsack to a typical knapsack problem, which has a simple greedy algorithm.

Using the following notations

• $L_s$ is the block serialized size limit.
• $L_c$ is the block consumed cycles limit.
• $s_t$ is the serialized size of a transaction
  $t$ in the block^[1], and
• $c_t$ is its consumed cycles.

The virtual bytes

$b_t$ is

$$b_t=max(\frac{c_t{L}_s}{L_c},s_t).$$

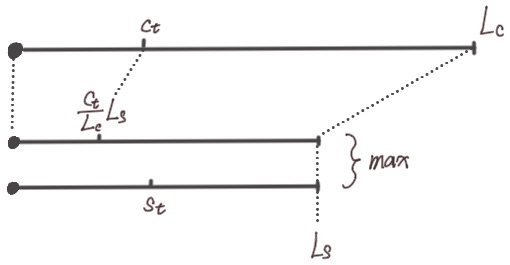
The greedy algorithm sorts the transactions in decreasing order of fee rate,

$R_t=F_t/b_t$ in which

$F_t$ is the fee paid by the transaction

$t$. It then proceeds to insert them into the block as long as there is remaining space of both serialized size and consumed cycles.

Ancestor Weight and Selection Algorithm

A transaction A is a parent of another transaction B if at least one of B's input cells is A's output cell. B is called a child transaction of A.

An ancestor of a transaction is either its parent transaction or an ancestor of any its parent.

Miners are not allowed to add a transaction to the next block unless all its ancestors are already in the chain or will be added to the next block together.

Instead of sorting the transactions by fee rate and try them one by one, miners have to process transactions in packages.

The ancestor package

$A[t]$ of a transaction

$t$ is a set that includes itself and all its ancestors remaining in the pool. The weight of the ancestor package

$W_{A[t]}$ is the lesser of the transaction fee rate and the package fee rate as defined in the following formula, where

• $b_t$ is the virtual bytes of a transaction
  $t$.
• $F_t$ is the fee it pays.

$$W_{A[t]}=min(\frac{F_t}{b_t},\frac{\sum _{i\in A[t]}{F}_i}{\sum _{i\in A[t]}{b}_i})$$

A modified algorithm sorts the transactions by ancestor weight and inserts the package as a whole.

• Create a block. Initialize the remaining size and cycles by subtracting space occupied by the cellbase.
• Make a clone of the pool so the loop below will not modify the pool.
• Repeat until the cloned pool is empty:
  • Find the transaction with the largest ancestor weight in the cloned pool.
  • Remove these transactions from the cloned pool.
  • Test whether the block has enough size and cycles space for all the transactions.
  • If space is enough, add the transactions to the block and update block remaining size and cycles, and update the ancestor weight of the descendants of those just added transactions.

The algorithm has to scan all the transactions unless there is a perfect fit for the max size or cycles. If the block is nearly full, and there are consecutive failed tests, the algorithm can exit early.

Descendant Weight and Trim Algorithm

⚠️⚠️️️️️⚠️️️ This section is still a proposal, which may be not available in the current version of CKB.

A transaction B is a child of another transaction A if at least one of B's input cells is A's output cell.

A descendant of a transaction is either its child transaction or a descendant of any its child.

The descendant package

$D[t]$ of a transaction

$t$ is a set which includes itself and all its descendants also in the pool. The weight of the descendant package

$W_{D[t]}$ is the greater of the transaction fee rate and the package fee rate as defined in the following formula, where

• $b_t$ is the virtual bytes of a transaction
  $t$.
• $F_t$ is the fee it pays.

$$W_{D[t]}=max(\frac{F_t}{b_t},\frac{\sum _{i\in D[t]}{F}_i}{\sum _{i\in D[t]}{b}_i})$$

Because of the physical limit, the node cannot save all unconfirmed transactions in the pool. In CKB, the pool has both the size and cycle limit. When the pool reaches the limit, it must trim the transactions using the descendant weight.

• Repeat until the pool size and cycles do not exceed the limits.
  • Find the transaction with the lowest descendant weight in the pool.
  • Remove the whole descendant package of the transaction from the pool and update the descendant weight of the ancestors of the just removed transactions.

Fee Bumping

Because transaction weight depends on its fee rate and its package fee rate, there are two corresponding methods to bump the fee.

• CPFP, Child Pay For Parent, bumps fee by increase the package fee rate.
• RBF, Replace By Fee, bumps fee by replacing the low fee rate transaction with a high fee rate one.

CPFP

A CPFP transaction is a child transaction of an existing transaction in the pool. To prioritize its parent, it must have a higher ancestor weight than its parent. Assume that the new transaction is

$q$, and its only parent transaction in the pool is

$t$, the CPFP transaction must have enough fee

$F_q$ such that

$$min(\frac{F_q}{b_q},\frac{F_q+\sum _{i\in A[t]}{F}_i}{b_q+\sum _{i\in A[t]}{b}_i})>min(\frac{F_t}{b_t},\frac{\sum _{i\in A[t]}{F}_i}{\sum _{i\in A[t]}{b}_i})$$

The CPFP transaction usually has a high fee rate, so it also bumps the descendant weight of its parent transaction thus they are less unlikely to be trimmed when the pool is full.

However, when a package is too large, the chance that it fails to fit into the remaining block space increases. The pool must limit the package transaction count, total serialized size, and the total consumed cycles.

• $L_{an}$ The max number of transactions in the ancestor package.
• $L_{ab}$ The max virtual bytes of all the transactions in the ancestor package.
• $L_{dn}$ The max number of transactions in the descendant package.
• $L_{db}$ The max virtual bytes of all the transactions in the descendant package.

If a transaction has outputs for different parties, one party can add new descendant transactions to pin the transaction with a very low descendant weight. Because of the descendant package limits, other parties cannot bump the fee rate via CPFP.^[2] It's a serious problem for protocols like lighting network.^[3]

CPFP carve-out^[4] is a solution to this problem. It allows exceeding the descendant package limits when the last transaction added to the package meets the following criteria.

⚠️⚠️️️️️⚠️️️ CPFP carve-out is still a proposal, which may be not available in the current version of CKB.

• The transaction has one ancestor in the pool.
• The transaction virtual bytes is at most
  $L_{cb}$.

CPFP carve-out allows at most one extra transaction. If the descendant package of a transaction has

$L_{dn}+1$ transactions, the pool should reject new descendants.

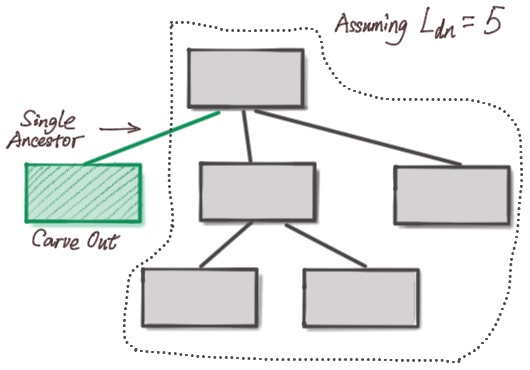
If all the parents of a transaction have been confirmed and the transaction has two outputs for each party, neither party can trigger the carve-out because only the direct child satisfies the condition "The transaction has one ancestor in the pool", but a single child is far from reaching the package limits. If a party adds more descendants, another party is always able to add an extra carve-out child to bump the fee.

RBF

⚠️⚠️️️️️⚠️️️ RBF is still a proposal, which may be not available in the current version of CKB.

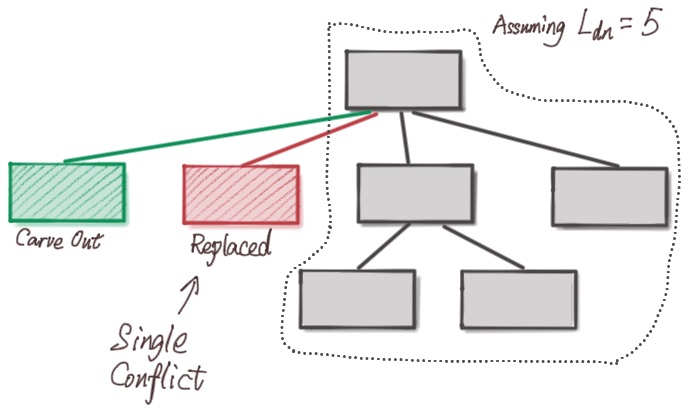
An RBF transaction has conflict inputs with existing transactions in the pool. Miners must remove all the conflict transactions and their descendants before accepting the RBF transaction, so the transaction creators must pay enough fees as incentives.

Using C to denote the set of conflict transactions and their descendants, the RBF transaction

$t$ must pay the fee

$F_t$ that

• Its fee rate
  $F_t/b_t$ is greater than or equal to any transaction in C.
• Its fee is greater than the total fee of all the transactions in C plus
  $b_t\ast R_b$, where
  $R_b$ is the minimal bumping fee rate.

The RBF transaction should not break the package limits. But some packages may have an extra transaction because of CPFP carve out, RBF carve-out reserves their limits if the new transaction has a single conflict transaction which has no descendants. When RBF carve out takes effect, any ancestor of the new transaction is allowed to have a descendant package that

• It has at most
  $L_{dn}+1$ transactions.
• The total virtual bytes is at most
  $L_{db}+L_{cb}$.

Recall that

$L_{dn}$,

$L_{db}$ are descendant package transactions count, total virtual bytes limits.

$L_{cb}$ is carve out transaction virtual bytes limits.

---

1. In CKB, it is the transaction molecule serialized size plus 4 bytes overhead. ↩︎

2. Bitcoin Optech. Transaction pinning. https://bitcoinops.org/en/topics/transaction-pinning/ ↩︎

3. Bitcoin Optech, New attack against LN payment atomicity. Bitcoin Optech Newsletter #95. https://bitcoinops.org/en/newsletters/2020/04/29/#new-attack-against-ln-payment-atomicity ↩︎

4. Bitcoin Optech. CPFP carve out. https://bitcoinops.org/en/topics/cpfp-carve-out/ ↩︎