# 拯救機概
## 大家應該知道怎麼用吧 不懂的人看這裡 [Hackmd語法大全](https://hackmd.io/@eMP9zQQ0Qt6I8Uqp2Vqy6w/SyiOheL5N/%2FBVqowKshRH246Q7UDyodFA?type=book)
[數學的打法](https://math.meta.stackexchange.com/questions/5020/mathjax-basic-tutorial-and-quick-reference)

目錄
===

# Ch8 基礎演算法
:::success
概念: 提出有效率解決問題的一種方式
定義: 有其先後順序、明確步驟、產生結果、有限時間內結束
演算法的三種結構：循序、選擇、重複
:::

UML 統一塑模語言，以圖畫方式表示 ex:案例圖、狀態圖
persudocode 虛擬程式碼，一種代碼的表示方式，但只有大略簡寫而已

----------
### (一) 排序

1. 選擇排序 Seletion sort

[圖示化影片](https://youtu.be/g-PGLbMth_g?si=YTmV4qJdF0njJdlf)

程式碼範例:

def selection_sort(deta):
    for i in range(len(deta)- 1):
        for j in range(i,len(deta)):
            m = max(deta)+1#表示很大的值
            if deta[j] < m:
                m = deta[j]
                index = j
        deta[i],deta[index] = deta[index],deta[i]
    return deta

nums = [2,1,3,5,4]
selection_sort(nums)

2. 泡沫排序 Bubble sort

[圖示化影片](https://youtu.be/xli_FI7CuzA?si=_Qtosz-MGNGdKhcs)

程式碼範例:

def bubble_sort(nums):
    n = len(nums)
    for i in range (n-1):
        for j in range (n-i-1):
            if nums[j] > nums[j+1]:
                temp = nums[j]
                nums[j] = nums[j+1]
                nums[j+1] = temp

nums = [2,1,3,5,4]
bubble_sort(nums)

3. 插入排序 Insertion sort

[圖示化影片](https://www.youtube.com/watch?v=JU767SDMDvA)

程式碼範例:

def insertion_sort(nums):
    n = len(nums)
    for i in range(1,n):
        for j in range (i,0,-1):
            if nums[j] < numd[j-1]:
                nums[i],nums[i-1] = nums[i-1],num[i]
            else:
                break
    return nums

nums = [2,1,3,5,4]
insertion_sort(nums)
#以上排序後都為[1,2,3,4,5]

### (二) 搜尋
:::info
Problem：
$$
如何在五個數中找到最大or最小整數，那有10^9個數呢?
$$
#hint 資料結構 Array(在python中稱為list)
:::
1. 循序搜尋(暴力法) Sequential search
* 最大的數

n = [1,2,3,4,5]
ans = -1 #答案
for i in n:
    if i>ans:
        ans = i

* 最小的數

n = [1,2,3,4,5]
ans = 10**10 #答案
for i in n:
    if i>ans:
        ans = i

* 懶人法

n = [1,2,3,4,5]
min_ans = min(n)
max_ans = max(n)

:::info
練習
請在2秒內建立一個1000000以內的質數表，並計算出有幾個質數
hint [埃拉托斯特尼篩法](https://zh.wikipedia.org/zh-tw/%E5%9F%83%E6%8B%89%E6%89%98%E6%96%AF%E7%89%B9%E5%B0%BC%E7%AD%9B%E6%B3%95)
:::

2. 二分搜尋法 Binary search
:::warning
當你的資料量很大怎麼辦? 這時候需要二分搜尋法幫你找問題了
注意! 只有在資料經過排序之後才能夠使用
:::

n=[1,2,3,4,5] #需先排序
left=0 #最左項
right=len(n)-1 #最右項
while left<=right:
    mid=(left+right)//2
    #切一半後判斷
    if n[mid]>target:
        right=mid-1 #超過取左邊串
    elif n[mid]<target:
        left=mid+1 #未達取右邊串
    elif n[mid]==target:#找到目標
        return mid 

$$
二分搜速度是非常快的，當你有n=10^{10}個資料的時候，大概只需要跑\log_2 n次迴圈就可以找到答案。
$$

### (三) 遞迴 Recursion
定義: 演算法中出現演算法本身（反之，為反覆式）白話文:重複呼叫自己
優點: 程式精簡
缺點: 速度慢，不容易實作，需要透過大量練習才能掌握

:::warning
使用python實作時只能遞迴3000次，超過記憶體會爆
解決方法:
import 標準函式庫sys 中的setrecursionlimit

import sys
sys.setrecursionlimit(100000)#可自由增加遞迴次數，太大扔會造成memory error

:::

以自訂義函式實作
ex: 1+2+3+....+n-1

def g(n):
    if n<0:
        return 0
    return g(n-1)+n
#g(10) = 55

**Tower of Hanoi（河內塔)**
* Problem: move n disks from A to C
* Rules
* Move one disk at a time
* Cannot place a larger disk onto a smaller disk

簡易規則：小盤子一定要在大盤子上面，一次只能移動一個
:::info
* How to move n disks?

* How many moves in total?
$$2^{n-1}+1次$$
:::

* To move n disks from A to C (for n > 1):

1. 移動 Disk 1~n-1 form A to B
2. 移動 Disk n from A to C
3. 移動 Disk 1~n-1 from B to C

#sudo code
Hanoi(n, src, dest, spare)
	if n == 1 # base case
		Move disk from src to dest
        else # recursive case
		Hanoi(n-1, src, spare, dest)
		Move disk from src to dest
		Hanoi(n-1, spare, dest, src)

實作

def Hoi(n,a,b,c):
    if n ==0:
        print(f"desk {n} from {a} to {c}")
    else:
        Hoi(n-1,a,c,b)
        print(f"desk {n} from {a} to {c}")
        Hoi(n-1,b,a,c)
    Hoi(10,"a","b","c")
    

**GCD(輾轉相除法)**

#a>b
def GCD(a,b):
    if a%b==0 :
        return(b)
    else:
        return(GCD(b,a%b))

**費氏數列(Fibonacci)**

def Fib(n):
    if n==1 or n==2:
        return(1)
    else:
        return(Fib(n-1)+Fib(n-2))


### 外傳 stack

#### ps.很佔記憶體

--------------------------------------------------------------

# Ch9 程式語言
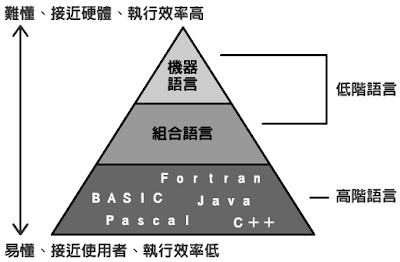
### 演化
1. 機器語言(0與1位元樣式所構成)
2. 組合語言Assembly(符號語言symbolic)
:::info
* 二進位碼->指令，記憶體位址->符號or助憶碼
* 組譯器(assemlber)程式：符號碼轉機器碼
:::
3. 高階語言
依解決問題的方法分為4種：程序式、物件導向式、函數式、宣告式
- 程序式 : C, Fortran, COBL, BASIC, Pascal, Ada
- 物件導向式 : c++, c#, JAVA, python, Visual Basic, Smalltalk
- 函數式 : LISP, Scheme
- 宣告式 : prolog


~~外傳 [x86 compiler](https://onecompiler.com/assembly/3w22x43ev)~~

### 高階程式語言
1. 為了解決難以讀懂程式碼的問題
2. 通常為直譯或編譯方式轉譯成機器語言

### 轉譯
1. 編譯 Compilation：整個轉譯
2. 直譯 Interpretation：逐行轉譯，有兩種
:::info
第一種：Java前的，逐行轉譯為對應電腦的機器語言，並立即執行
第二種：Java開始，先編譯成位元組碼，並於有 JVM 的電腦執行
:::

### 原始程式的轉譯處理
1. 語彙分析器（lexical analyzer）：讀入符號，並產生符記（tokens）
2. 語法分析器（syntax analyzer）：將符記剖析為指令
3. 語意分析器（semantic analyzer）：檢查產生的指令，確保語意不會產生混淆
5. 程式碼產生器（code generator）：將其轉換為一組機器語言所構成的指令，以供電腦執行

### 物件導向(使用python實作)
#### 範例 建立使用者跟使用者id

class User:
    # Attribute
    def __init__(self,user_id,username): 
        self.id = user_id
        self.name = username
        self.follower = 0 #Attribute 可以預設，也可以內建
        self.following = 0
    #Method
    #Method always need to have self parameter 
    def follow(self,user):
        user.follower += 1
        self.following += 1

user_1 = User("11211109","daidai0000")
#print(user_1.id,user_1.name)
#print(user_1.follwer)
user_2 = User("777","taro")

user_1.follow(user_2)
print(user_1.follower)
print(user_1.following)

print(user_2.follower)
print(user_2.following)
# 可以拿去執行看看

:::danger
##### CH10老師跳過
:::
# CH11 資料結構Data Structure
## 函式中資料的傳遞 - 傳值，傳址，傳參考
:::info
* 引數（argument）~~又稱實際參數(實參，actual parameter)~~
是主程式用於「呼叫函式」，也就是「執行函式」時的「輸入值」
* 函式內的參數（parameter）~~又稱形式參數（形參，formal parameter）~~
是用於「函式的宣告」，也就是定義函式
:::
1. 傳值(pass by value):把值「複製」到函式中
2. 傳址(pass by address):傳遞記憶體位址
* ##### 事實上pass by address也是在傳值，只不過這個值剛好是記憶體位址(指標)
3. 傳參考(pass by reference):類似傳址，但不會分配記憶體給參數x、y，所需記憶體較少
4. 二維陣列到多維陣列

5. struct
* 特性
* first in first out
* 像疊積木一樣一層一層
* 經典範例 (請看CH8 合內塔演算法)
*

7. link-list(鏈結串列)
:::info
鏈結串列(Linked List)常用來處理相同類型資料，在不連續的記憶體位置，以隨機的方式儲存，由於不用事先宣告一塊連續記憶體空間，所以較不會造成記憶體的浪費。
由許多節點組成，每個節點包含**資料欄**與**指標欄**，指標欄會指向下一個資料所在的記憶體位置。因此再追加或刪除資料相當方便，因為只需要更動指標的指向，但在讀取資料就會較費時，因為必須從串列的頭開始尋找。
:::
* 實作
:::danger
以上由chat-gpt生成，可能果會跟預期結果不太一樣
(基本上還是看得懂，好像也沒差)
:::

class Node:
    def __init__(self, data):
        self.data = data
        self.next_node = None


class LinkedList:
    def __init__(self):
        self.head = None

    def is_empty(self):
        return self.head is None

    def append(self, data):
        new_node = Node(data)
        if self.is_empty():
            self.head = new_node
        else:
            current_node = self.head
            while current_node.next_node:
                current_node = current_node.next_node
            current_node.next_node = new_node
    def delete(LinkedList, current_node, pre):
        if pre == None:
        # 如果 pre 為 None，表示要刪除的是鏈結串列的第一個節點
        # 將 LinkedList 更新為 cur 節點的下一個節點，即將頭指針指向下一個節點
            LinkedList = current_node.next_node
        else:
        # 如果 pre 不為 None，表示要刪除的是中間或尾部的節點
        # 將 pre 節點的 next 指向 cur 節點的下一個節點，即跳過 cur 節點
            pre.next_node = cur.next_node
        return LinkedList
    
    def display(self):
        current_node = self.head
        while current_node:
            print(current_node.data, end=" -> ")
            current_node = current_node.next_node
        print("None")
        
    # Create a linked list
    my_linked_list = LinkedList()

    # Append elements to the linked list
    my_linked_list.append(1)
    my_linked_list.append(2)
    my_linked_list.append(3)

    # Display the linked list
    my_linked_list.display()

:::info
執行結果 1 -> 2 -> 3 -> None
:::
-----------------------------------------------
# Ch12 抽象資料型態ADT
:::warning
複雜抽象資料型態:
* 串列：list
* 堆疊：stack，後進先出(Last In First Out LIFO)
* 佇列：quene，先進先出(First In First Out FIFO)
:::
## Stack 堆疊
1. 限制性的線性串列
2. 增加和移出都在頂端(先進後出)
3. 資料的存取必須符合LIFO
### 運算格式
* stack(stackName)：建立空堆疊
* push(stackName,deta_whichin)：在頂端推入元素
* pop(stackName,deta_whichdelete)：刪除頂端元素，可被使用或被丟棄
* empty(stackName)：檢查堆疊是否為空的
### 應用
* 反轉資料：完整建立堆疊後再pop輸出
* 配對資料：
#### stack 經典應用例子一
以作業十的「1,2,3」數字序列為例，要輸出以下數字的步驟為:
* 123: push 1, pop, push 2, pop, push 3, pop
* 132: push 1, pop, push 2, push 3, pop ,pop
* 213: push 1, push 2, pop, pop, push 3, pop
* 231: push 1, push 2, pop, push 3, pop, pop
* 312: 無法產生
* 321: push 1, push 2, push 3,pop, pop, pop

括號匹配問題 現在有一堆左括號跟右括號，現在你要判斷他能不能符合數學上的表示方式
simpal input

(((())))))
((((()))))
((((((((())))))))

simpal ouput

no
yes
no

## Queue 佇列
1. 先進先出 FIFO：
輸入順序:123 輸出順序:123


## 樹上演算法
:::warning
nodes(節點)：根、樹葉、內部節點
root(根)：最上面沒有進入弧線的節點
leaves(樹葉)：最下方的節點
internal nodes(內部節點)：如其名，是在中間的節點
arcs(弧線)：連結節點的線
path(路徑)：一連串弧線
child(子)：從一個已知節點可以直接存取的節點
parent(父)：可以直接存取子的節點
siblings(兄弟)：有共同的父的節點
descendents(後代)：全部可被同個節點到達的節點
ancestor(祖先)：全部可到達同個節點的節點
subtree(子樹)：一個節點的所有子和每個子的後代，一個子和他的後代算一個子樹
:::
### BST(二元樹)
##### DFS(深度優先)
前序 (preorder), 中序 (inorder) 和後序 (postorder) 是指遍歷二元樹 (binary tree) 時，父節點相對於左右節點的順序。
假設二元樹如下：

4 #4為根
/ \
2 6 #2、6為內部節點
/ \ / \ #123為左子樹，246為右子樹
1 3 5 7 #1、3、5、7為樹葉
則三種遍歷的順序依序為：

* 前序 (preorder): 中 -> 左 -> 右，4213657
* 中序 (inorder): 左 -> 中 -> 右，1234567
* 後序 (postorder): 左 -> 右 -> 中，1325764
:::danger
對二元搜尋樹 (binary search tree, BST) 做 inorder traversal 就是由小到大依序遍歷。
:::
例子

stack=[reference link]
rpn=['1','2','3','*','+']
for i in range (len(rpn)):
    if rpn[i] not in {'+','-','*','/'}:
        node=Node(rpn[i])
        stack.append(node)
    else:
        node=Node(rpn[i])
        node.right=stack.pop()
        node.left=stack.pop()
        stack.append(node)
bet=stack,pop()

##### BFS(Breadth-First 廣度優先)
4 #4為根
/ \
2 6 #2、6為內部節點
/ \ / \ #123為左子樹，246為右子樹
1 3 5 7 #1、3、5、7為樹葉
順序：4->2->6->1->3->5->7
#### GRAPH(圖)
#### 四則運算(應用)
利用二元樹概念處理運算問題
ex: 1+2*3 => 1 2 3 * + (輸入數字，遇符號先計算後兩者數字

---------------------------------------------------
# CH8 資訊安全(全華那本
## 基本原則 CIA
資料機密性(Confidenriality)：防治未經授權第三者
資料完整性(Integrity)：避免遭到竄改
系統可用性(Availability)：確保資料、系統可即時提取
不可否認性(Non-Reputation)：提供訊息傳送方與接受方的交易證明
## 其他需求
信賴性(authenticity)：資料本身或來源可被驗證
究責性(accounability)：確保資料的不可否認性，提供可靠的紀錄

## 資料機密性：對稱式加密 vs. 非對稱式加密
:::warning
密碼法(crypotography)
加密法(ciphers)
加密(encryption)
解密(decryption)
明文(plaintext)
密文(ciphertext)
:::
### 對稱式金鑰密碼加密法(Symmteric-key ciphers，密鑰加密法):
:::info
加解密時使用相同密鑰
:::
#### 方法
##### 傳統對稱式：
1. 替換式加密：用一個符號替換另一個符號
* 移位密碼(加密時將每個符號往前後移N格) ex:凱薩加密法
* 替換密碼(製作一個轉換表) ex:[跳舞小人密碼](https://codepen.io/anie116/full/jdzvJK)
2. 區塊式加密：多個等長的模組（block），各區塊各自加解密
* 事先約定一個短字串當作秘密ex:ENIGMA
* XOR運算(先轉換二進位利用XOR進行加密，再轉ACSII code)

IV加密
IV初始向量

運作方式
搭配區塊式
會在內容中添入文本(增加複雜度)
#### 優點
簡單好用，是一個有效率又省錢的方案
#### 缺點
易破解(被攔截到金鑰)

### 非對稱式金鑰密碼加密法(Asymmetric-key ciphers，公鑰密碼加密法):
:::info
兩組密碼:一組加密，一組解密
公鑰(Public key):公開(大家都知道)
私鑰(Private key):隱藏(個人)
:::
常見應用
1. 加密
2. 數位簽章Digital Signature(私鑰簽章，公鑰驗證)
3. 密碼交換
:::danger
加解密的鑰匙要是完整一對(pair)的，所以可以是公鑰加密私鑰解密，也可以是私鑰加密公鑰解密，沒有一定。
:::
ex:RSA, Diffie-Hellman
#### 基本原理
[圖片來源](https://medium.com/@RiverChan/%E5%9F%BA%E7%A4%8E%E5%AF%86%E7%A2%BC%E5%AD%B8-%E5%B0%8D%E7%A8%B1%E5%BC%8F%E8%88%87%E9%9D%9E%E5%B0%8D%E7%A8%B1%E5%BC%8F%E5%8A%A0%E5%AF%86%E6%8A%80%E8%A1%93-de25fd5fa537)
使用數學上的難解問題(以下為例子)
離散:給定二數$x$和$y$
例子:給$x^y$，求$x$、$y$
因數分解：給定二個質數$p$和$q$
例子:給定$pq$，求$p$、$q$
### RSA加密演算法
#### 優點
1. 可配合對稱式加密運算
#### 缺點
1. 大量運算
2. 耗時特長

假設甲乙加換密碼
兩者有著共同密碼
第三者難以計算出(目前)
例子:
甲密碼為$x^a$除以$q$的餘數，乙密碼為$x^b$除以$q$的餘數
共同密碼:$x^{a+b}$除以$q$的餘數

## 資料完整性
驗證密碼是否被修改
例子:雜湊函數

### 雜湊函數(HashTable Function)
任意長度字串運算後，得到固定長度的雜湊函數

#### 應用
1. 驗證資料傳輸是否無誤
2. 訊息驗證碼(MAC)
#### 優點
1. 高敏感度(微小改動，結果不同)
2. 單向函數(無法回推)
3. 不易發生碰撞(不同輸入，不易得到相同結果)

### HMAC基本概念
傳送端和接受端共享一組密碼(驗證來源，目的地正確性)
實際配合其他參數，避免被不同類型的網路攻擊

### 數位簽章

確認資料是來自特定使用者
特定使用者，使用其私要進行簽章

### PGP加密(雙層加密)
利用會議金鑰進行加密
會議金鑰使用公開金鑰加密

### PGD解密
先用公鑰解密，在使用會議金鑰解密出密文

### 公開金鑰管理
集中式管理
PKI
CA(憑證授權中心)認證公鑰

分散式管理:Web of Trust

故障偵測機制:常用<心跳機制>

## 8-5網路攻擊
目的
未經許可的存取
中斷服務氣正常運作
<駭客>
hacker:專精某領域的專家