# Week 4:CTC
###### tags: `技術研討`
## 論文部分
### ㄧ、介紹(Introduction) - 信賢
- **論文前言**
現實中的序列學習任務輸入資料大多是雜訊(noisy)、未分段資料(unsegmented input data)而對標籤序列(label sequences)進行預測。 例如在語音識別中聲音訊號被轉錄為單詞。 遞歸神經網絡(RNN)是強大的序列學習器,非常適合此類任務。 但受限於以下兩點,本文提出了一種新的訓練方式讓RNN來直接標記未分段序列的方法,從而解決了這兩個問題。
- 需要提供給它預先分段的訓練資料
- 輸出轉換為標籤序列的後處理步驟
- **為什麼要使用CTC(Connectionist temporal classification)**
在傳統的語音識別的聲學模型訓練中,對於每一幀的資料,我們需要知道對應的標籤(label)才能進行有效的訓練,在訓練資料之前需要做語音對齊的預處理。對齊的預處理要花費大量的人力和時間,而且對齊之後,模型預測出的標籤(label)又只是區域性分類的結果,而無法給出整個序列的輸出結果,往往要對預測出的label做一些後處理才可以得到我們最終想要的結果。

上圖是「你好」這句話的聲音的波形示意圖, 每個紅色的框代表一幀資料,傳統的方法需要知道每一幀的資料是對應哪個發音音素。比如第1,2,3,4幀對應「n」的發音,第5,6,7幀對應「i」的音素,第8,9幀對應「h」的音素,第10,11幀對應「a」的音素,第12幀對應「o」的音素。(這裡暫且將每個字母作為一個發音音素)
再比如,在OCR中使用RNN時,RNN的每一個輸出要對應到字符圖像中的每一個位置,要手工做這樣的標記工作量太大,而且圖像中字符數量不同,字體樣式不同,大小不同,導致輸出不一定能和每個字符一一對應。
- **讓我們的神經網路自己去學習對齊方式**
CTC(Connectionist temporal classification,連結時序分類)就是為了剛剛上述所遇到的問題。與傳統的聲學模型訓練相比,採用CTC作為損失函式的聲學模型訓練,是一種完全端到端(end to end)的聲學模型訓練,不需要預先對資料做對齊,只需要一個輸入序列和一個輸出序列即可以訓練。這樣就不需要對資料對齊和一一標註,並且CTC直接輸出序列預測的概率,不需要額外的後處理。
CTC的方法是關心一個輸入序列到一個輸出序列的結果,那麼它只關心預測輸出的序列是否和真實的序列是否接近(相同),而不會關心預測輸出序列中每個結果在時間點上是否和輸入的序列正好對齊。
- **舉例來說**
例如輸入一個200幀的音頻數據,真實的輸出是長度為5的結果。經過神經網絡處理之後,出來的還是序列長度是200的數據。真實輸出結果都是nihao這5個有序的音素,但是因為每個人的最佳特點不一樣,例如,有的人說的快有的人說的慢,原始的音頻數據在經過神經網絡計算之後,第一個人得到的結果可能是:nnnniiiiii ... hhhhhaaaaaooo(長度是200),第二個人說的話得到的結果可能是:niiiiii ... hhhhhaaaaaooo(長度是200)。這兩種結果都是正確的計算結果,可以想像,長度為200的數據,最後可以對應上nihao這個最佳順序的結果是非常多的方法。
### 二、在 CTC 發表前,主要的 label sequence 框架 - 立晟
#### Hidden Markov Models (HMMs)

- 摘要
- 由內部「狀態」(states)之間的轉換以及各狀態呈現的「觀察值」(observations)來描述整個資料的模型
- 觀察值:現象、事件這種可以直接觀測到的資訊
- 隱狀態:無法觀察到的部份
- 舉例
- 假設杰恩很好奇雅筑今天是走路還是騎車來上班,但他又懶得問,這時候他就假設走路或騎車是內在狀態 (看不到的),然後藉由觀察雅筑來上班時會不會喘,進而推論今天雅筑是走路還是騎車來上班
<!-- - 假設小明很好奇在不同天氣的時候外面的人吃冰淇淋的狀況是如何,但是小明又很懶得出門看天氣,這時候他就假設天氣(晴天、陰天、雨天)是內在狀態(看不到),然後藉由持續觀察路人有沒有吃冰淇淋,進而推論外面天氣的變化狀況 -->
- 限制
- 如果特徵資料是連續性的數值 (e.g., 位置、角度),則必須在進行訓練或辨識前,先將資料做分群或分類,轉換為離散的符號序列
- RNN 可以處理連續性的數值
- 需要特定領域的專業知識 (e.g., 語音有聲學模型、發音模型、語言模型等)
- 無法處理連續重複出現的字元 (e.g., apple 將被識別為 aple)
- CTC 用 blank 解決
<!-- - 可能會預測出訓練集中沒有出現過的結果 (適合應用在資料量少的情形) -->
#### End-to-end Models
- 修正了哪些問題
- 將多個模組用一個網絡聯合訓練,使用同一個評價指標更容易找到全局最優解
- 不要求特徵序列與標籤序列一一對齊
<!-- |項目別\框架|HMMs|RNN|
|-|-|-|
|狀態|離散,以隨機變數表示|連續,可向量表示|
|時間|離散|離散|
|內在狀態|不可被觀察|不可被觀察|
|外在狀態|可被觀察|可被觀察|
|補充||允許在每個時間點給輸入<br>引入非線性| -->
<!-- - 參考來源
- https://medium.com/ai-academy-taiwan/hidden-markov-model-part-2-ac46dcdd42d1
- https://yuehhua.github.io/2018/07/21/why-rnn/
- https://ir.nctu.edu.tw/bitstream/11536/73101/1/751001.pdf -->
### 三、數學符號區 - 立晟
|符號|說明|
|-|-|
|L|所有要預測的字元<br>e.g., {A,B,C,...,1,2,3,...}|
|L'|L 加上空字元<br>e.g., {A,B,C,...,1,2,3,...,-}|
|X|所有 input sequence 集合|
|Z|所有 output sequence 集合|
|x|X 當中的一個例子|
|z, $l$|Z 當中的一個例子 (x 的 output,z,$l$ 的長度不得大於 x 的長度)<br>e.g., cat|
|$l'$|Z 當中的一個例子,並在每個字元前後加上空字元 ($\epsilon$)<br>e.g., $\epsilon$ c $\epsilon$ a $\epsilon$ t $\epsilon$|
|S|符合 input 是 X 、 output 是 Z 的訓練集|
|ED(p, q)|將 p 轉為 q 所需的最小次數|
#### 補充-編輯距離 (edit distance)
- 編輯距離越小,兩個字串的相似度越大
- 什麼情況下,編輯距離會+1?
– 將一個字元替換成另一個字元
– 插入一個字元
– 刪除一個字元
參考連結:https://www.itread01.com/content/1542024732.html
|符號|說明|
|-|-|
|LER|加總每個 x 經縮放後的編輯距離,再除以 x 總數|
|$π$|各種可能的 CTC 路徑|
|$B$|將路徑中連續的相同字元刪減為 1 個並刪去空白字元|
### 四、CTC 基本概述 - 立晟
- 首先將空字元加入分類所有可能的字元,讓空字元也可能是 frame 預測的結果
- $L′$ = {a,b,c,...,x,y,z} ∪ {−} = $L$ ∪ {−} = {a,b,c,...,x,y,z,−}
- 預測完每條路徑 ($\pi$) 各個 frame 的結果後,會將路徑中連續的相同字元刪減為 1 個並刪去空白字元 (−)
- $B(\pi1)=B(−−stta−t−−−e)=state$
- $B(\pi2)=B(sst−aaa−tee−)=state$
- $B(\pi3)=B(−−sttaa−tee−)=state$
- $B(\pi4)=B(sst−aa−t−−−e)=state$
- 最後將預測結果一樣的機率累加起來 (不管走哪條路徑,只要最後預測結果是 $l$ 就好)
- $p(l|x) = \sum_\limits{B(\pi)=l} p(\pi|x)$
- 假設每個字元的條件機率是彼此獨立的 (儘管事實並非如此),一條路徑的機率就是每個字元機率的乘積
- $p(\pi|x) = \prod\limits_{t=1}^T y^t_{\pi_t}$
- $\pi_t$:output sequence 在 t 時間對應的字元
- 在語音識別中,有時同一種發音會有多種拼寫,/greɪt/ 可能拼成great 也可能拼成grate。這兩種拼法中的各個字元就不是條件獨立的。如果第三個字元選擇了 e,那麼第四、五個字母就必須選擇 at。而 CTC 就無法建模這種依賴關係,常常給出 grete 這樣雜糅的拼寫
- 若有 T 個位置,每個位置有 n 種選擇(L'的大小),那麼就有 $n^T$ 種可能,這樣時間複雜度太可怕了,所以 CTC 借用了 HMM 中的前向後向算法(forward-backward algorithm)來計算
### 五、CTC 中的前向後向算法 (計算推導) (昱睿、昊中)
#### 前向後向算法
* 從CTC基本概述可知,若要窮舉出所有可能路徑需要花費大量的時間。透過前向後向算法進行計算可以將問題透過動態規劃(Dynamic Programming, DP)進行分解。
* 前向算法
* 首先定義 $\alpha$
* $\alpha_t(s)\equiv\sum_\limits{\pi\in N^T:B(\pi_{1:t})=\textbf{l}_{1:s}}\prod\limits_{t'=1}^{t} y^{t'}_{\pi_t'}$
* $\alpha_t(s)$ 表示從可能的起始點累積到 $t$ 時刻且 $ℓ′=s$ 的總機率。式子的右邊簡單描述的話,為加總所有能將 $\pi_{1:t}$ 映射到 $\textbf{l}_{1:s}$ 各種的路徑 $\pi$,而這些 $\pi$ 是由路徑上各點的機率相乘所求得的。也就是 **$\pi$ 的前 $t$ 項針對 $\mathcal{B}$ 對應過去會和 $\textbf{l}$ 的前 $s$ 項會一樣**
* 分解 $\alpha_t(s)$
* 因為會一項一項地計算,所以我們可以將 $\alpha_t(s)$ 分解成從 $t-1$ 時刻往下一個時刻而來的
* 故 $\alpha_t(s)$ 可以寫成 $\alpha_{t-1}(s)$ 與 $\alpha_{t-1}(s-1)$ 的組合
* 其中 $\alpha_{t-1}(s)$ 就是 $t-1$ 時刻映射後 label 的前 $s$ 個和 $\textbf{l}$ 相同的機率;$\alpha_{t-1}(s-1)$ 就是 $t-1$ 時刻映射後 label 的前 $s-1$ 個和 $\textbf{l}$ 相同的機率。
* 設定初始值
* $\alpha_1(1)=y^1_b$
* $\alpha_1(2)=y^1_{\textbf{l}_1}$
* $\alpha_1(s)=0,\forall s>2$
* 表示沒有足夠的時刻去完成sequence $s$
* 得到 $\alpha$ 的遞迴式
* $\alpha_t(s)= \begin{cases}\alpha_{t-1}(s)+\alpha_{t-1}(s-1)y_{l'_s}^t\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{if}\ \ l'_s=b\text{ or }l'_{s-2}=l'_s\\ \left [ \alpha_{t-1}(s)+\alpha_{t-1}(s-1)+\alpha_{t-1}(s-2) \right ] y_{l'_s}^t \ \ \ \ \ \ \ \text{otherwise}\end{cases}$
* 有了初始值以及遞迴式,我們透過DP將想求的得$\alpha_t(s)$逐步分解至初始值的地方,進而求得$\alpha_t(s)$的總機率。
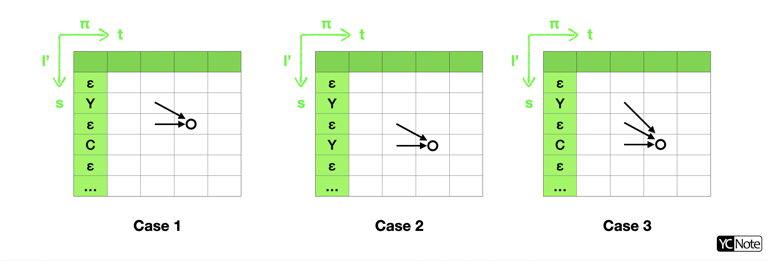
* 後向算法
* 後向算法與前向算法非常類似,後向算法是希望求出從 $t$ 時刻開始累積到 $T$ 時刻,所有能將 $\pi_{t:T}$ 映射到 $\textbf{l}_{s:|\textbf{l}|}$ 各種的路徑 $\pi$ 的機率,故也可分解並求得與前向算法概念向相同的初始值與遞迴式。
* 初始值
* $\beta_T(|\textbf{l}'|)=y^T_b$
* $\beta_T(|\textbf{l}'|-1)=y^T_{\textbf{l}_{|\textbf{l}|}}$
* $\beta_T(s)=0,\forall s<|\textbf{l}|-1$
* 遞迴式
* $\beta_t(s)= \begin{cases}\beta_{t+1}(s)+\beta_{t+1}(s+1)y_{l'_s}^t\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{if}\ \ l'_s=b\text{ or }l'_{s+2}=l'_s\\ \left [ \beta_{t+1}(s)+\beta_{t+1}(s+1)+\beta_{t+1}(s+2) \right ]y_{l'_s}^t \ \ \ \ \ \ \ \ \text{otherwise}\end{cases}$
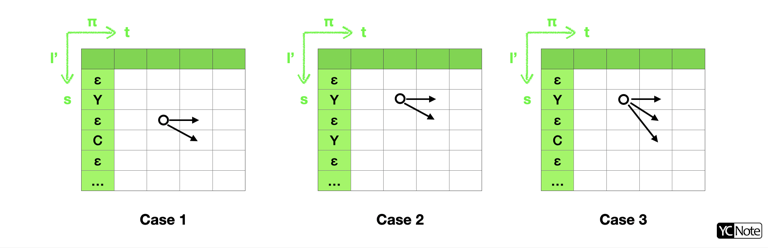
- 為了避免前向後向算法因機率乘積越來越小導致 underflows,我們可以將 $\alpha_t(s),\ \beta_t(s)$ 進行 rescale:
- $C_t$ 的意思是所有路徑 $\pi$ 經過 $\mathcal{B}$ 後的前 $s$ 個字會跟 $\textbf{l}$ 的前 $s$ 個一樣的機率
$$\hat{\alpha}_t(s)\equiv\frac{\alpha_t(s)}{C_t},\ C_t\equiv\sum_\limits{s}\alpha_t(s)\ \ \ and\ \ \ \hat{\beta}_t(s)\equiv\frac{\beta_t(s)}{D_t},\ D_t\equiv\sum_\limits{s}\beta_t(s)$$
#### 訓練 CTC
現在已知有一個 RNN ($\mathcal{N}_w$),我們想要求出他在 $S$ 這個訓練集的梯度向量是多少。其中 objective function 是
$$\mathcal{O}^{ML}(S, \mathcal{N}_w)\, =\, -\sum_\limits{(\textbf{x}, \textbf{z})\in S}ln(p(\textbf{z}|\textbf{x}))$$
所以我們想要算這個東西
$$\frac{\partial\mathcal{O}^{ML}(S,\, \mathcal{N}_w)}{\partial y^t_k}$$
因為微分跟加法可以交換,所以我們只要先算出這個就好
$$\frac{\partial ln(p(\textbf{z}|\textbf{x}))}{\partial y^t_k}$$
其中 $\textbf{x}$ 為某個 RNN 預測出來的值,$\textbf{z}$ 就是這個 $\textbf{x}$ 的正確 label。
先思考一個點:在要預測成 $\textbf{l}$ 的路徑 $\pi$ 中,會在前 $t$ 個時間會被預測成 $\textbf{l}_{1:s}$ ($\textbf{l}$ 的第 $s$ 個位置)的機率是起始點到 $t$ 的乘積,再乘上從時間 $t$ 開始到時間 $T$ 結束的乘積就是整個路徑。就是 $\pi$ 被預測成
$\textbf{l}$ 的機率 (每個字元的機率彼此條件獨立 (conditionally independent)),所以算是會這樣呈現
$$\alpha_t(s)\beta_t(s)\, =\, \sum_\limits{\pi\in A_{t, s}}y^t_{\textbf{l}'_s} \prod\limits_{t=1}^T y^t_{\pi_t} \;,\; A_{t,s}\, =\, \left\{\pi \in \mathcal{B}^{-1}(\pi):\pi_t\, =\, \textbf{l}'_s \right\}$$
因為 $p(\pi|x) = \prod\limits_{t=1}^T y^t_{\pi_t}$,所以上式代換並移項可以改寫成
$$\frac{\alpha_t(s)\beta_t(s)}{y^t_{\textbf{l}'_s}}\, =\, \sum_\limits{\pi\in A_{t, s}}p(\pi|x)$$
我們要求得 $\frac{\partial ln(p(\textbf{z}|\textbf{x}))}{\partial y^t_k}$ 中的 $p(\textbf{z}|\textbf{x})$,可以透過加總所有的 $s$ 而求得,所以
$$p(\textbf{z}|\textbf{x}) = \sum_\limits{s=1}^{|\textbf{l}'|} \frac{\alpha_t(s)\beta_t(s)}{y^t_{\textbf{l}'_s}}$$
而我們考量時刻 $t$ 經過 label $k$ 的路徑可以定義為 $lab(\textbf{l}, k)=\{s:\textbf{l}'_s=k\}$(表示所有 $s$ 位置出現labe $k$ 的集合),所以
$$p(\textbf{z}|\textbf{x}) = \sum_\limits{s\in lab(\textbf{l}, k)} \frac{\alpha_t(s)\beta_t(s)}{y^t_k} + \sum_\limits{s\notin lab(\textbf{l}, k)} \frac{\alpha_t(s)\beta_t(s)}{y^t_k}$$
現在我們只需要針對 $y^t_k$ 去偏微分即可在訓練時進行backpropagation 了
$$\frac{\partial ln(p(\textbf{z}|\textbf{x}))}{\partial y^t_k}\, =\, \frac{1}{p(\textbf{z}|\textbf{x})}\frac{\partial p(\textbf{z}|\textbf{x})}{\partial y^t_k}$$
從上述算式我們可以右邊 $p(\textbf{z}|\textbf{x})$ 這個東西的微分會長這樣
$$\frac{\partial p(\textbf{z}|\textbf{x})}{\partial y^t_k}\, =\, \frac{\partial}{\partial y^t_k} \sum_\limits{s\in lab(\textbf{l}, k)} \frac{\alpha_t(s)\beta_t(s)}{y^t_k} = -\frac{1}{(y^t_k)^2}\sum_\limits{s\in lab(\textbf{l}, k)}\alpha_t(s)\beta_t(s)$$
$$= -\frac{C_t D_t}{(y^t_k)^2}\sum_\limits{s\in lab(\textbf{l}, k)} \hat{\alpha}_t(s)\hat{\beta}_t(s)$$
另一方面,
$$\frac{1}{p(\textbf{z}|\textbf{x})} = \frac{1}{\sum_\limits{s=1}^{|\textbf{l}'|} \frac{\alpha_t(s)\beta_t(s)}{y^t_{\textbf{l}'_s}}} = \frac{1}{C_t D_t \sum_\limits{s=1}^{|\textbf{l}'|} \frac{\hat{\alpha}_t(s)\hat{\beta}_t(s)}{y^t_{\textbf{l}'_s}}} = \frac{1}{C_t D_t Z_t}$$
其中
$$Z_t = \sum_\limits{s=1}^{|\textbf{l}'|} \frac{\hat{\alpha}_t(s)\hat{\beta}_t(s)}{y^t_{\textbf{l}'_s}}$$
所以整個乘起來會變成
$$\frac{\partial ln(p(\textbf{z}|\textbf{x}))}{\partial y^t_k}\, =\, 1 - \frac{1}{Z_t (y^t_k)^2}\sum_\limits{s\in lab(\textbf{l}, k)}\hat{\alpha}_t(s)\hat{\beta}_t(s)$$
(其實我自己在推倒的時候前面的 1 不見了QQ)
如果把變 normalized 的話就會變成這樣
$$\frac{\partial ln(p(\textbf{z}|\textbf{x}))}{\partial u^t_k}\, =\, y^t_k - \frac{1}{Z_t y^t_k}\sum_\limits{s\in lab(\textbf{l}, k)}\hat{\alpha}_t(s)\hat{\beta}_t(s)$$
* 小問題:為什麼在這篇論文只算到對 $y^t_k$ 偏微分就好;而不是算到對 $w_k$ (RNN 的權重) 去微分?
#### Time Complexity
* CTC loss 的 time complexity 是 <font color='blue'>**$O(T)$**</font>
$T$: 最大字元數,在 code 裡面就是 **max_char_width**
* 參考出處: [Connectionist Temporal Classification with Maximum Entropy Regularization
](https://papers.nips.cc/paper/2018/file/e44fea3bec53bcea3b7513ccef5857ac-Paper.pdf)
### 六、CTC 的預測 - 沛筠
Classifier 的 output:機率最高的 labelling。
$$h\left(x\right)=\underset{l\in L^{\leq T}}{arg\: max}\: p(l|x)$$
#### 各種 Inference 的優缺點
- Greedy Decoder (Best Path Decoding):假設時間點 t 相互獨立,機率最高的路徑對應於機率最高的 labelling。
$$h(x)\approx B(\pi^*),\:\:\: \pi^*:\underset{\pi\in N^t}{arg\: max}\: p(\pi|x)$$
- 沒有考慮到 input-output 是多對一的關係,因此不保證找到的 labelling 無誤。
- 比如,aa- 和 aaa 個別的機率低於 bbb,但兩者相加後的機率卻高於 bbb。
- 時間複雜度:$O(t)$
- Beam Search Decoder:每個時間點 t 下,計算連續的 labelling prefix 機率,並選取前 W 高的節點繼續擴展。
W:beamSize
<br>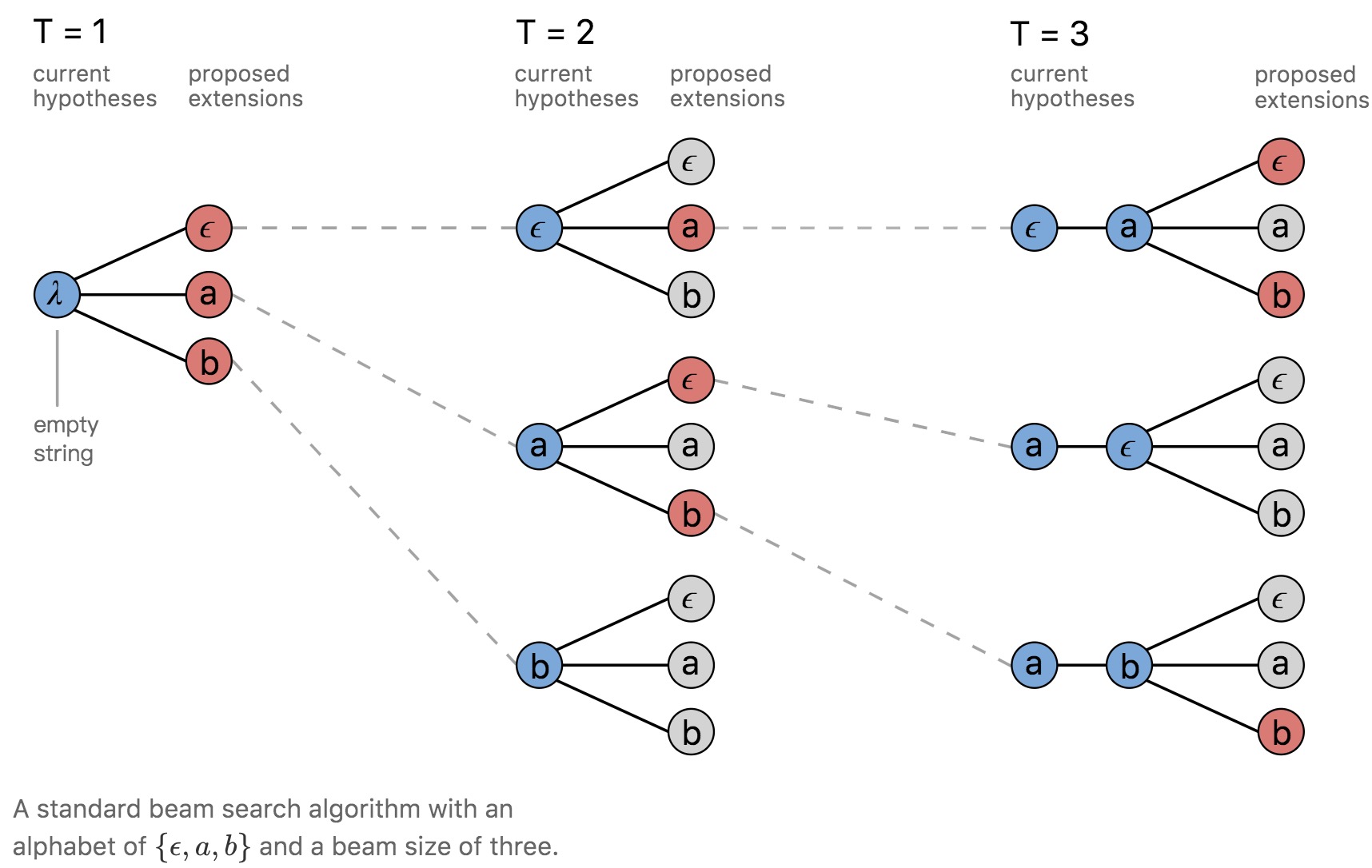
<br>
- 不同路徑可能映射至相同預測結果(如 T=3 時選出的 -ab 和 abb 映射後將為 ab )。
- 時間複雜度:$O(t\times beamSize\times L’\times log(beamSize\times L’))$
- <font size=2>$\pi_{t+1} = \pi_{t}+beamSize\times L’\times log(beamSize\times L’)$</font>
- 得到 <font size=2>$beamSize\times L’$</font> 條路徑後,需再選出機率前 <font size=2>$beamSize$</font> 高的預測結果保留。
- [參考連結](https://xiaodu.io/ctc-explained-part2/)
- Prefix Beam Search Decoder:每個時間點 t 下,計算「已合併重複 label 且去除 blank」的連續 labelling prefix 機率,並選取前 W 高的節點繼續擴展。
<br>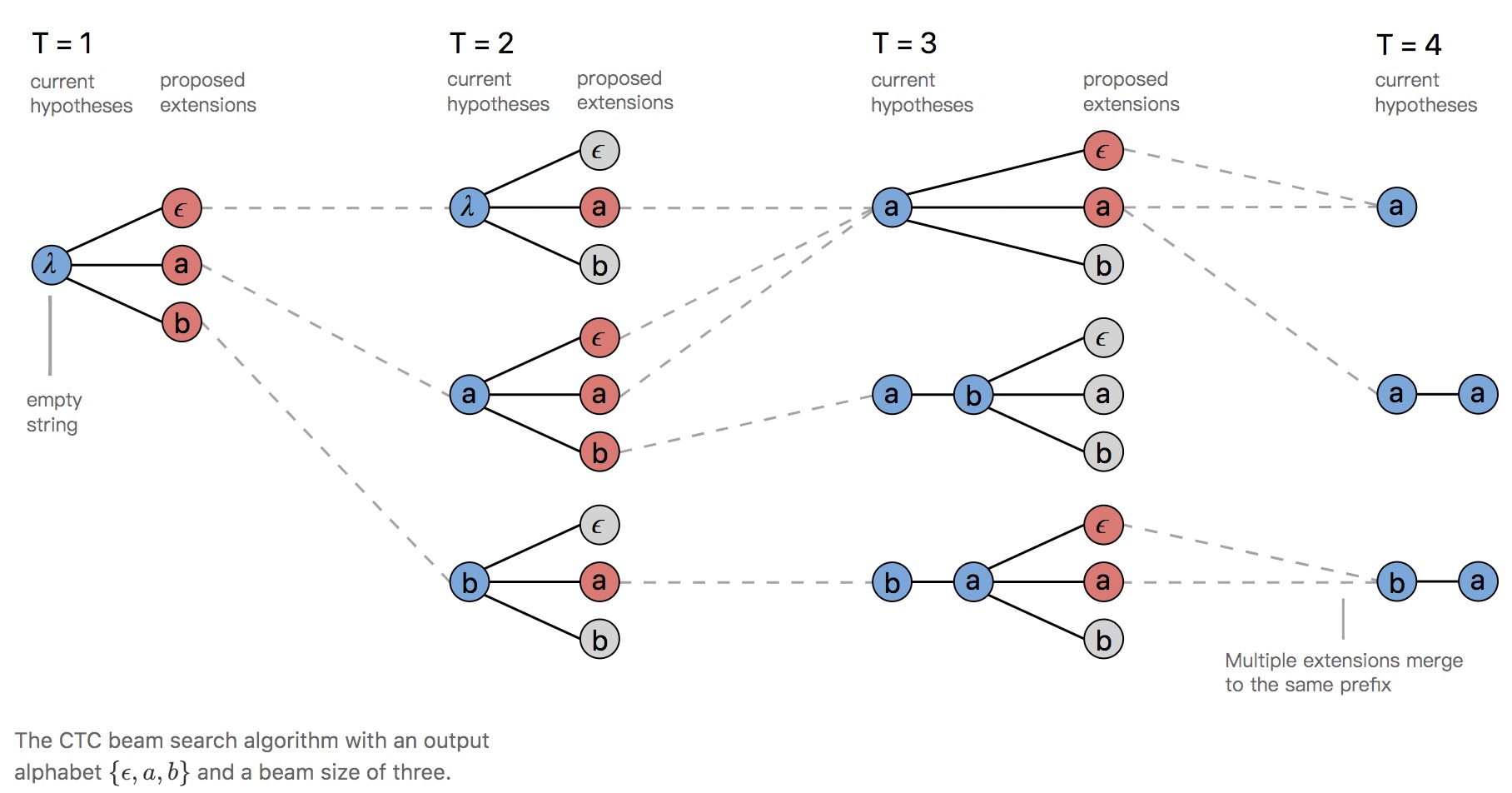
<br>
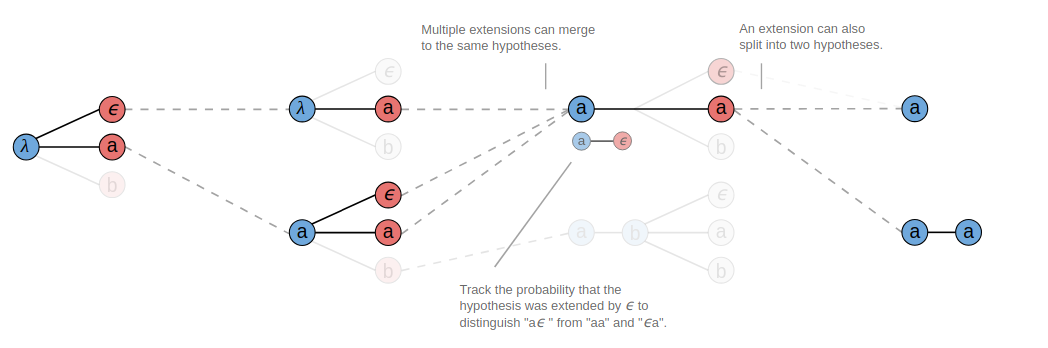
- 相較於 Beam Search Decoder,它能保留更多種預測結果(路徑)。
- T=3 時,合併 a、a- 與 aa 為 a 進行計算。
- 回溯 prefix a 的「成因」,並於 T=4 時得到 a 及 aa 兩種結果。
- 時間複雜度:$O(t\times beamSize\times L’\times log(beamSize\times L’))$
- [參考連結1](https://medium.com/corti-ai/ctc-networks-and-language-models-prefix-beam-search-explained-c11d1ee23306)
- [參考連結2](http://placebokkk.github.io/asr/2020/02/01/asr-ctc-decoder.html)
- 補充部分
- [時間複雜度 參考連結](https://zhuanlan.zhihu.com/p/39266552)
- [Inference 參考連結](https://distill.pub/2017/ctc/)
## 程式碼解析 (大重點)
```python=
tensorflow==1.13.1
```
### 1. ctc_loss (信賢)
#### 參數說明
```python=
def ctc_loss(labels,
inputs,
sequence_length,
preprocess_collapse_repeated=False,
ctc_merge_repeated=True,
ignore_longer_outputs_than_inputs=False,
time_major=True):
```
- **labels**:int32類型的稀疏向量(SparseTensor)
稀疏矩陣是相對密集矩陣而言的,密集矩陣就是我們常見的矩陣,如果密集矩陣大部分數都是0,那麼就沒有必要浪費空間來存這些爲0的數據,我們只要將那些不爲0的索引、值和形狀記錄下來,就可以大大節省內存空間,這個就是稀疏矩陣。稀疏矩陣在Tensorflow中的結構如下,
:::success
SparseTensor(indices, values, dense_shape)
:::
- indices:就是密集矩陣中不爲0的數的索引。
- value:是一個list,存儲的是密集矩陣中對應上面indices索引中的值。
- dense_shape:密集矩陣的形狀。
labels.indices[i, :] == [b, t]
表示 labels.values[i]儲存了第幾個`batch`(b)還有`time`(t).
而Tensorflow中,將稀疏矩陣還原成密集矩陣的方法也很簡單,使用sparse_tensor_to_dense函數即可。
- **inputs**:3維的浮點向量(float Tensor)
- if time_major=True,其格式為 [max_time,batch_size,num_classes]
- if time_major=False,其格式為 [batch_size, max_time, num_classes]
::: info
把LSTM輸出的第0維和第1維換一下即可
:::
- **sequence_length**:是1維的int32向量,尺寸為batch_size,裡面每個值的大小為sequence的長度。
- **preprocess_collapse_repeated**:
- 類型:Boolean.
- 默認: False
- 說明:若為True,則在loss計算之前運行預處理步驟,其中傳遞給loss的重複標籤會合併為單個標籤。如果訓練數據是強制對齊得到的,會包含不必要的重複。簡言之,是否需要預處理,將重複的 label 合併成一個。
- **ctc_merge_repeated**:
- 類型:Boolean.
- 默認:True
- 說明:如果為False,那麼伴隨ctc計算的深入,重複的非blank將不會被合併,會被解釋為獨立的labels。 這是CTC的簡化(非標準)版本。
- 排列組合:
::: info
- preprocess_collapse_repeated=False, ctc_merge_repeated=True:
經典CTC,輸出帶有重複標籤的中間帶有blanks類別,也可以通過解碼器解碼,輸出不帶有blanks的重複類別。
- preprocess_collapse_repeated=True, ctc_merge_repeated=False:
不輸出重複的類別,因為它們訓練前在輸入標籤中就已經合併。
- preprocess_collapse_repeated=False, ctc_merge_repeated=False:
輸出重複的中間帶有blank的類別,但是通常不需要解碼器合併重複項。
- preprocess_collapse_repeated=True, ctc_merge_repeated=True:
未經測試。 很可能不會學習到輸出重複的類別。
:::
- **ignore_longer_outputs_than_inputs**:
- 類型:Boolean
- 默認:False
- 說明:如果True,輸出比輸入長的sequence將被忽略。
在默認的情況下,如果輸入inputs長度小於輸出預測序列的長度,那麼默認情況下,會報錯Not enough time for target transition sequence。
:::danger
如果為true,則CTCLoss將簡單地為這些返回零梯度項目,否則返回InvalidArgument錯誤,從而停止訓練。
:::
- **time_major**:
- 類型:Boolean
- 默認:True
- 說明:調整input格式的參數
- 用途:使用True(默認)會更有效率,因為它避免在ctc_loss計算的開始處轉置。 然而大多數TensorFlow數據都是批量處理的,因此通過此功能還可以接受以批處理形式輸入。
```python=
if not time_major:
inputs = array_ops.transpose(inputs, [1, 0, 2]) # (B,T,N) => (T,B,N)
```
- **Returns**:是一個1維的float向量,尺寸為`batch`,使用-log代表機率。
返回值為 $loss$ ,其數學式為$loss = -\log(p(l|x))$,範圍介於0到無限大之間。
機率是指 $p(l|x) = \sum_\limits{B(\pi)=l} p(\pi|x)$,其範圍介於0到1之間,越靠近1代表準確率越高。
也可將此式改寫成 $p(l|x) = e^{-loss}$
:star:我們舉個範例想一下:star:
當 iteration = 0,$loss=55$,則 $p(l|x)=e^{-55}$ $\approx$ 0
當 iteration = 1000,$loss=0.001$,則 $p(l|x)=e^{-0.001}$ $\approx$ 1
- **Raises**:
當labels不是稀疏向量(SparseTensor)
```python=
if not isinstance(labels, sparse_tensor.SparseTensor):
raise TypeError("Expected labels (first argument) to be a SparseTensor")
```
- **Notes**:
此為執行softmax操作,因此輸入應是,舉例像是LSTM對輸出的線性投影。
輸入張量(tensor)最裡面尺寸大小是`num_classes`,表示num_labels + 1,其中num_labels是真實標籤的數量,以及最大值((num_classes-1))保留用於空白標籤。
例如,對於包含3個標籤“ [a,b,c]”的詞彙表,
“ num_classes = 4”,標籤索引為“ {a:0,b:1,c:2,blank:3}”。
- **Input requirements**:
:::info
sequence_length(b) <= time for all b
max(labels.indices(labels.indices[:, 1] == b, 2))
<= sequence_length(b) for all b.
:::
- (1) sequence_length(b)<=所有b的時間意味着minibatch中每個例子的序列長度應該小於或等於time
- (2) labels.indices [:, 1]指代的是batch這一維,labels.indices [:, 2 ]指代的是這一維,這個意思就是指輸出不能大於輸入。
### 2. ctc_beam_search_decoder (昱睿)
```python=
def ctc_beam_search_decoder(inputs: tf.Tensor,
sequence_length: list,
beam_width=100,
top_paths=1,
merge_repeated=True):
```
* **inputs**
- 類型:tf.Tensor
- 默認:無
- 例如:tf.placeholder, tf.nn.bidirectional_dynamic_rnn 這樣函數得輸出值
- 說明:調整 input 格式的參數
- 用途:在 CRNN.py 裡面使用這個函數的時候這裡放的是 logits,是一個經過 CNN + RNN 再經過 fully-connected layer,最後壓縮成 (max_image_width, number of classes) 這樣的形狀
* **sequence_length**: 序列長度
- 類型:list,然後裡面會是 int
- 默認:無
- 例如:[200]
- 用途:定義最大字元數
* 在 CRNN.py 裡面就是 self.seq_len,然後在 train 這個 method 裡面被令成是 [self.max_char_width] ,這個 list
* 在 run.py 就是 arg.max_image_width,也就是輸入圖片的最長寬度 (單位是 pixel)
* **beam_width**
- 類型:int
- 默認:100
- 用途:beam search 尋找的時候的寬度
- 特別說明
- 如果設成 1 的話,那就只有 1 格,因此就會跟 greedy 很像
- 一定要大於 0
* **top_paths**
- 類型:int
- 默認:1
- 用途:控制 output size
- 特別說明
- 一定要介於 0 ~ beam_width 之間
* **merge_repeated**
- 類型:Boolean
- 默認:True
- 用途:要不要把重複的字合併
- 說明:假設在 search 的結果 7 個 frame 分別為 A B B - B - B (- 為空白)
* True: A B (感覺語音比較會這樣選?)
* False: A B B B
* **Returns**
* decoded: 一個 tuple
* 第 0 個:輸出值 index
* 第 1 個:輸出值的 value
* 第 2 個:輸出值的 shape
* 例如:
```python
SparseTensorValue(indices=array([[0, 0],
[0, 1],
[0, 2],
[0, 3],
[0, 4]]), values=array([17, 33, 30, 26, 30]), dense_shape=array([1, 5]))
————————————————
版权声明:本文为CSDN博主「hjxu2016」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/hjxu2016/article/details/97780274
```
* log_probability: 形狀為 batch_size $\times$ top_paths 大小的 float 矩陣
* 參考資料: [link](https://blog.csdn.net/hjxu2016/article/details/97780274)
### 3. ctc_beam_search_decoder_v2 (昊中)
* tf.nn.ctc_beam_search_decoder_v2 (昊中)
```python=
def tf.nn.ctc_beam_search_decoder_v2(
inputs,
sequence_length,
beam_width=100,
top_paths=1
):
# Note, merge_repeated is an invalid optimization that is removed from the
# public API: it returns low probability paths.
return ctc_beam_search_decoder(inputs, sequence_length=sequence_length,
beam_width=beam_width, top_paths=top_paths,
merge_repeated=False)
```
Args:
`inputs`: 3維的浮點向量(float Tensor),尺寸為[max_time, batch_size, num_classes]。
`sequence_length`: 1維的int32向量,尺寸為batch_size。
`beam_width`: 為一個int的純量(>=0),beam search的寬度。
`top_paths`: 為一個int的純量(>=0、<=beam_width),控制輸出尺寸。
Returns:
一個tuple (decoded, log_probabilities)。
`decoded`: 長度為top_paths的list,decoded[j]為一個包含已解碼輸出(decoded_outputs)的稀疏矩陣。
`decoded[j].indices`: 為索引矩陣[total_decoded_outputs[j], 2],Rows存放[batch, time]。
`decoded[j].values`: 為values的向量,尺寸為[total_decoded_outputs[j]],儲存beam j的解碼分類結果。
`decoded[j].dense_shape`: 為shape的向量,尺寸為(2),其值為[batch_size, max_decoded_length[j]].
`log_probability`: 為包含sequence的log-probabilities的浮點矩陣(float matrix),尺寸為[batch_size, top_paths]。
* 參考資料: [link](https://github.com/tensorflow/tensorflow/pull/15586)
### 4. ctc_greedy_decoder (沛筠)
```python=
def tf.nn.ctc_greedy_decoder(
inputs, sequence_length, merge_repeated=True
):
```
<br>Args:
`inputs`:3D float tensor ( [max_time, batch_size, num_classes] ),為 logits 值
`sequence_length`:含有序列長度的 1D int32 vector ( size = batch_size )
`merge_repeated`:默認為 True,決定 decoder 結果是否合併重複 label
<br>Returns:
`tuple (decoded, neg_sum_logits)`
`decoded`:a single-element list,`decoded[0]`是包含預測輸出的 SparseTensor
`neg_sum_logits / log_probabilities`:a float matrix ( batch_size x 1 ),為找出的序列在各時間點 t 中最大 logit 之和的負數
[參考連結](https://www.w3cschool.cn/tensorflow_python/tf_nn_ctc_greedy_decoder.html)
* 主要說明函數中的參數怎麼設定,以及會有甚麼結果
### 5. Frame 的長度和 Output Sequence 之間的關係 - 立晟
:::danger
如果有誤,以下開放打臉
:::
以 Output Sequence 為 see 為例,假設 Frame 的數量為 4,CTC的路徑可能是:

這會出現一個問題,就是<font color='red'>相同的連續字元會被drop duplicate</font>
所以 frame 的長度應該大於等於 $2|l|+1$,讓每個字元之間空隙都可能預測為 blank (ε),而<font color='red'> frame 的數量取決於影像 input 時的寬,以及 CNN 的框架</font>,以 Week 1: CRNN + CTC 的 paper 為例,寬為 200 的圖經過 CNN 萃取特徵後,會變成了 49 個 frame ($frame 的數量 = width / 4 - 1$),所以如果影像中的文字數 ($l$) 超過 24 個,就應該放大影像的寬


### Reference
https://www.cnblogs.com/liaohuiqiang/p/9953978.html
https://zhuanlan.zhihu.com/p/43534801
https://www.itread01.com/content/1544337968.html
https://zhuanlan.zhihu.com/p/41331716
https://blog.csdn.net/JackyTintin/article/details/79425866
https://blog.csdn.net/weixin_39529413/article/details/103946375
## 提問區
#### 已關閉
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet