---
title: Traitement d'image
date: 10-02-2020
tags: Image, TIFO
---

# [TIFO] Traitement d'image

slides: http://jo.fabrizio.free.fr/teaching/ti/tifo_intro.pdf

## Introduction

Beaucoup de problématiques:
* extraction d'info
* restauration / amélioration
* ... (voir slides, plein d'exemples)

Applications:
* Vidéo surveillance (suivi de personnes, radars automatiques)
* Empreintes digitales
* Assistance
* Vision, conduite (assistance à la conduite)
* Art (restauration de film ancien, coloration automatique de film)
* Imagerie médicale, images satellites

> Problème éthique: qui va l'utiliser, comment et pourquoi

Arrivée du CMOS : 1969

Logiciels de traitement d'image ("des fois c'est quand même bien d'avoir ça"):
* GIMP (GNU Image Manipulation Program)
* Photoshop

Bibliothèques:
* Olena
* OpenCV
* ITK
* ...

### Evaluation

Certainement un QCM

En parallèle, probablement un projet/travail à faire avec Élodie

---

Slides cours 2 : http://jo.fabrizio.free.fr/teaching/ti/tifo_formation_image.pdf

## Perception, le retour

Ce matin (voir 1er cours de synthèse), on a vu les différents capteurs.

Visualisation:

**écran cathodiques (CRT)**: canon à éléctron

**LCD (Liquid Cristal Display)**: rétro éclairages + filtres par cristaux liquides

Les cristaux liquide: laisser passer ou pas la lumière
Premiers retro éclairages = néons
Puis remplacement des néons par des LED
puis matrices de led (chaque pixel = une led qui donne l'info)

Quelle importance ? Car selon l'écran ce qu'on voit n'est pas forcémment le réel.
Écrans plat : Encore pleins de défauts, notamment sur la résitution des couleurs

## Vision humaine, le retour

Fovéa, c'est là où y'a le plus de capteurs (perception de la couleur)

Pas de différence entre un rayon orange et deux rayons vert et rouge

Codage de la couleur sur 2 octets:
* 5 bits pour le rouge
* 5 bits pour le bleu
* 6 bits pour le vert (toujours le fait qu'on perçoit mieux le vert)

Notre perception est logarithmiaue, variable dans le temps (notre vision des couleurs dépent de ce que l'on a vu avant)
Ainsi que du filtrage et la subjectivité de chacun. Notre cerveau filtre plein de détails inutiles.

Le prof illustre ça avec des illusions d'optiques rigolotes.

Notre cerveau extrapole dans le temps.

**Il faut des critères objectifs pour qualifier des résultats** (c'est le seul but de cette partie).

évaluation fausse = pire que pas d'évaluation

---
Slides cours 3 : http://jo.fabrizio.free.fr/teaching/ti/tifo_codage_coul.pdf

## Codage de la couleur

### Modèle RGB


Modèle basé sur la perception humaine (couleurs primaires en synthèse additive) mais pas très intuitif pour choisir les couleurs (sauf pour Manuel Tertre).

### Modèle HLS (Hue, Lightness, Saturation)


Pléthore de variantes.

Trois composantes:
- Teinte (= Hue, la couleur, angle sur le disque de couleur "pure")
- Luminance (assombrir/éclaircir)
- Saturation (centre = faible saturation, extrémités = forte saturation); degré de "pureté" (est-ce que la couleur est pétante ou pas)

**Avantage** bien plus intuitif pour "pick une couleur"
**Défaut** beaucoup de variantes (notamment HSV, Hue, Saturation, Value)

Dépend du contexte, qu'est ce qui s'adapte le mieux, ce qui est imposé ?

### Modèle CMY (Cyan, Magenta, Yellow)


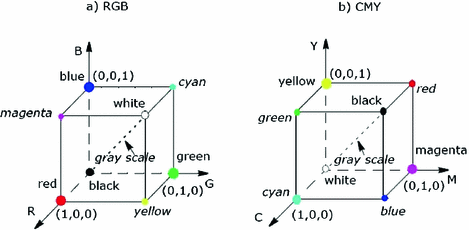
Utile pour l'impression (synthèse soustractive). Mais pas très utile en traitement d'image, semble-t-il (Fabrizio l'a jamais utilisé).

### Niveau de gris (Grayscale)

Juste une valeur allant de 0 à 255, par exemple.

L'échelle n'est pas linéaire, ce qui amène à beaucoup d'erreurs (on ne peut pas faire de combinaison linéaire).

### Autres espaces

- YIQ
- Lab
- XYZ
- YCbCr
- ...

Pourquoi nous emmerder avec ça ? Parce que la première question qu'on doit se poser est:
> Quel est l'encodage que l'on chosit?

## Conversions

C'est utile mais pénible.

### RGB à ...

Aller voir les slides

### RGB à niveau de gris

Première idée ne correspondant pas exactement à la perception humaine mais rapide:
$$
L = (r + v + b) / 3
$$

Correspondant à la perception humaine, mais lent (calcul sur flottants):
$$
L = 0.299r + 0.587v + 0.114b
$$

### RGB à noir et blanc

Plus un problème "philosophique": la solution dépend du besoin.

## Représentation de l'image

**Pixel**: pictures element
**Voxel**: volume element

### Représentation en matrice

L'image étant une matrice de pixels, on représente l'image par une matrice:
Chaque case de la matrice étant un vecteur de l'espace de couleur choisi

> Deux représentations en mémoire possibles: matrice ou vecteur

**Discrétisation spatiale**: très jolie mot pour la résolution
**Echantillonnage**: amplitude des valeurs (sur combien de bits code-t-on chaque canal de la couleur)

:::info
**Tips** : Savoir faire des puissances de 2.
:::

### Autres représentations

D'autres méthodes peuvent être utiles en traitement d'images:
* arbres (bien pour les filtres, par exemple)
* graphes

### Maillage

D'autres maillages que le maillage carré des pixels classiques (qui ne sont pas forcémment pertinents).

Par exemple, maillage héxagonal (gros avantage: tous les voisins sont à la même distance), mais difficulté techniques pour les fabriquer.

Maillage carré : 4-connexe ou 8-connexe?
Problème topologique sévère avec le maillage carré ([Théorème de Jordan](https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Jordan))

### Exemple d'arbre: max tree


## Formats

Pléthore de formats: JPEG, TIFF, PNG, ...

Dépend totalement du cas d'usage: par exemple JPEG n'est pas idéal pour le traitement (perte de données) mais utile dans d'autres cas (car très léger).

D'autres critères: compression, avec ou sans palettes, libre ou pas, ...

**TIFF**: beaucoup de fonctionnalités mais complexe à décoder
**PNM** (ou PPM): très facile à décoder mais très très lourd
**TGA**: selon Fabrizio, bon compromis entre facile à décoder et qualité

(On a déjà utilisé le format ppm pour raytracer)

## Traitement d'image

### Changement d'illumination

**Première idée**: simplement augmenter chaque composante en RGB ou Grayscale.

Mais mauvais car l'échelle n'est pas linéaire: la multiplication est plus adaptée.

### Correction d'illumination non uniforme à partir d'une référence

La division donne de meilleurs résultats que la différence.

### Modification de l'organisation spatiale des images

On ne part pas de l'origine pour calculer la destination, mais on part de l'image destination et on calcule la valeur pour chaque pixel à partir de l'origine.

Si on va chercher l'antécédant, on ne va pas forcémment tomber sur un pixel précis. Comment faire ? Plusieurs solutions possibles:
* Prendre le plus proche voisin. Solution de mauvaise qualité
* Faire une interpolation bilinéaire (moyenne pondérée)
* Faire une interpolation bicubique: comme linéaire, mais au lieu de prendre deux points, on en prend 4, ce qui donne un polynome (d'où le nom)

---
Slides cours 3 : http://jo.fabrizio.free.fr/teaching/ti/tifo_histo.pdf

## Histogrammes

On regarde tous les échantillons et compte combien d'échantillons ont la même valeur.

**Exemple**: compter les pixels en fonction de leur valeur en niveau de gris

Donne une vision globale de l'image, et non une information spatiale.
On peut prévoir des informations sur l'image avec l'histogramme, par ex:
* si elle est plutôt sombre
* si elle est peu ou beaucoup contrasté

### Analyse et correction à partir de l'histogramme

#### Equilibrer l'histogramme

On peut rééquilibrer l'histogramme avec une correction linéaire: par exemple si l'image est plutôt sombre et a des valeurs allant de 0 à 120, on va rééquilibrer ces valeurs entre 0 et 255. Les pixels ayant une valeur au-dessus de 120 seront saturés et auront pour valeur 255 (blanc).

Cet algorithme perd donc des informations (pour les pixels saturés). Néanmoins, sans même connaître la photo, on sait que cela augmentera le contraste.

**Autre courbes**

On peut utiliser n'importe quelle fonction pour faire la correction, comme par exemple, log ou exp.

La correction linéaire à des défauts car il ne prend pas en compte la forme de l'histogramme. Certaines solutions existent.

#### Equilibrer avec un histogramme cummulé

On veut augmenter le contraste là où l'histogramme cumulé a une "pente" (dérivée) très forte.


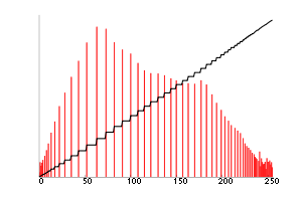
:::info
À voir chez soi
:::

On essaie de rendre l'histogramme cumulé linéaire donc l'histogramme plat.

Avec une égalisation d'histogramme, on perd moins de détails qu'avec un étirement linéaire

Il existe de nombreuses variantes de cet algorithme.

CLAHE

#### Histogramme en couleur

*Première question* : Quel espace de couleur ?

Plusieurs possibilités :
* faire un histogramme 3D ; assez précis mais beaucoup de traitement
* traiter les 3 canaux RGB de manière décorrélée, semble être une idée assez mauvaise car "créé de nouvelles couleurs"
* utiliser HSV mais ne modifier que le canal contraste (ou d'autres codages de couleurs)

### Histogramme: indexation

**Comparaison d'image** Histogramme invariant par de nombreuses transformations, notamment par rotation.

Mais si il y a une légère translation de l'histogramme (changement de l'intensité lumineuse), la comparaison est catastrophique. La distance *bin-to-bin* résoud ce problème.

Distances possibles :
* Bin by bin (colonne à colonne)
* Cross-bin

**Exemple d'application**: en encodage vidéo, certaines frames sont des "key-frame" avec l'ensemble de l'image, d'autres sont encodées par différence. L'analyse de l'histogramme est un bon moyen de savoir quand placer une key-frame.

### Application d'histogramme en 3D

**Tentative de réduction du nombre de couleur**: utile pour simplifier l'analyse de l'image par la suite.

*Algorithme utilisé*: [médiane cut](http://www.tsi.telecom-paristech.fr/pages/enseignement/ressources/beti/quantif_couleur/algMC.html)

Etapes:
1. Construction de l'histogramme des couleurs
2. Eliminer les extrémités vides (couleurs non utilisées)
3. Couper selon une dimension (R, G ou B) en fonction de la médiane: il y a autant de pixel d'un côté que de l'autre
4. On recommence à l'étape 3 avec une autre dimension

Le cube est alors séparé en n sous cube, représentant chaque nouvelle couleur. La couleur finale pourra par exemple être le barycentre. Beaucoup de stratégie possible.

**Binarisation** cet algorithme peut être utilisé pour faire de la binarisation (on ne coupe qu'une seule fois). Néanmoins, la recherche de seuil est un problème encore difficile.

**L'algorithme d'Otsu** est un algorithme de référence pour la binarisation.

Néanmoins, ces techniques ne prennent un compte que l'image globalement, et néglige l'aspect spatial (qui est pourtant pertinent pour la binarisation). Cela ne marche donc que pour les cas assez simple.

Critères locaux beaucoup utilisés: [Niblack et Sauvola](https://scikit-image.org/docs/dev/auto_examples/segmentation/plot_niblack_sauvola.html), basés sur la moyenne et l'écart type.

**Diffusion de l'erreur avec [FloydSteinberg](https://fr.wikipedia.org/wiki/Algorithme_de_Floyd-Steinberg)**
> Lors de la réduction du nombre de couleurs d'une image (par exemple pour la conversion en GIF, limité à 256 couleurs), cet algorithme permet de conserver l'information qui devrait être perdue par la quantification en la poussant sur les pixels qui seront traités plus tard.

 pour chaque y de haut en bas
   pour chaque x de gauche à droite
      ancien_pixel := pixel[x][y]
      nouveau_pixel := couleur_la_plus_proche(ancien_pixel)
      pixel[x][y] := nouveau_pixel
      erreur_quantification := ancien_pixel - nouveau_pixel
      pixel[x+1][y  ] := pixel[x+1][y  ] + 7/16 * erreur_quantification
      pixel[x-1][y+1] := pixel[x-1][y+1] + 3/16 * erreur_quantification
      pixel[x  ][y+1] := pixel[x  ][y+1] + 5/16 * erreur_quantification
      pixel[x+1][y+1] := pixel[x+1][y+1] + 1/16 * erreur_quantification

"Puisque j'en suis là, autant continuer à spoil"

## Filtrage

[Slides](http://jo.fabrizio.free.fr/teaching/ti/tifo_filtrage.pdf)

### Exemples

#### Eliminer le bruit (lissage)

On peut faire une moyenne locale en appliquant le noyeau de convolution suivant:
$$
\frac{1}{9} \times
\begin{pmatrix}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{pmatrix}
$$

Plusieurs solutions pour appliquer sur la dernière ligne:
* utiliser une matrice 2x2
* considérer l'image comme cyclique
* oublier la dernière colonne/ligne
* dupliquer la dernière ligne/colonne

**Autres coefficient**

On peut donner des coéfficients en fonction de la distance, plutôt que de donner les mêmes poids aux pixels proches et éloignés. Exemple: gaussienne.

Donne un effet moins flou (mais améliorable).

**Filtre médian (débruitage)**

Trie le voisinage, prend la valeur mediane, et on retire les extremités. Coute cher mais donne de bon résultats.

Délire de Sami (*super pratique*):

allocate outputPixelValue[image width][image height]
allocate window[window width × window height]
edgex := (window width / 2) rounded down
edgey := (window height / 2) rounded down
for x from edgex to image width - edgex do
    for y from edgey to image height - edgey do
        i = 0
        for fx from 0 to window width do
            for fy from 0 to window height do
                window[i] := inputPixelValue[x + fx - edgex][y + fy - edgey]
                i := i + 1
        sort entries in window[]
        outputPixelValue[x][y] := window[window width * window height / 2]

**Filtre gaussien (le retour)** donne une impression de flou car attenue les frontières.

Au lieu de prendre en compte uniquement la distance spatiale (ce qui était déjà cool), on prend aussi en compte la distance des couleurs.
Ne marche pas pour le bruit impulsionnel (pixels très différents isolés).

Différentes implémentations du filtre gaussien séléctif:
* lazy (on ne prend en compte que si la distance est inférieure à un seuil)
* module le coefficient en fonction de la distance

**[Filtre de Nagao](http://www.tsi.enst.fr/pages/enseignement/ressources/mti/Tomita/nagao.htm)** au lieu de prendre un voisinage centré sur le pixel, on utilise plusieurs formes de voisinages en fonction de la position dans l'image.


Pour chaque pixels, pour chaque motifs, on calcul la variance, et on garde le motif avec la variance la plus faible.

#### Détecter les contours

Un contour est une transition brutale, dans une direction arbitraire. En pratique, les contours ne sont pas parfait (plusieurs pixels de transition), ce qui rend les choses plus difficiles.

Une solution pour la détection des contours est la dérivée: on fait une dérivée partielle sur chacun des axes (x et y).

Comme on est en discret, on fait une approximation:

$$
\lim\limits_{x\rightarrow x_0}\frac{f(x+x_0)-f(x)}{x-x_0}
$$
Ce qui donne en discret:
$$\frac{f(x+1)-f(x)}{1} = f(x+1)-f(x)$$

Ou alors
$$\frac{f(x+1) - f(x-1)}{2}$$
On peut approximer la détection de contours avec des filtres (ici avec Prewitt en x):
$$
\begin{pmatrix}
-1 & 0 & 1 \\
-1 & 0 & 1 \\
-1 & 0 & 1 \\
\end{pmatrix}
$$

**Les [filtres de Sobel](https://en.wikipedia.org/wiki/Sobel_operator)** peuvent aussi d'être utilisé pour la détection. Ils permettent de lisser l'image résultante (comme les filtres gaussiens).

Plusieurs stratégies pour retrouver les contours à partir du gradient:
* seuillage (techniques de binarisations vue au-dessus)
* seuillage par [hystérésis](https://fr.wikipedia.org/wiki/Hyst%C3%A9r%C3%A9sis) (**à connaitre**)
-> au lieu de rechercher un seul seuil, on en cherche deux:
- un seuil haut: recherche grossierement où est la forme
- un seuil bas: très precis mais récupère du bruis
On garde dans le seuil bas que les pixels qui sont dans une région (spatiale) qui contiennent au moins un pixel dans le seuil haut.
Rend beaucoup plus robuste les detections par seuil.

**[Filtres de Compass](http://fourier.eng.hmc.edu/e161/lectures/gradient/node5.html)** (prononcé compas): on convolue avec des filtres de Sobel tournés d'un quart de tour.

**[Filtres de Frei-Chen](http://rastergrid.com/blog/2011/01/frei-chen-edge-detector/)** (solution proche de Compass). A un coût plus élevé que Sobel, mais meilleur dans certains cas (plus robuste à différents niveaux d'illumination).

#### Filtres à dérivé seconde pour la détection de contour

**Calcul du laplacien** on obtient facilement (voir slides):
$$f''(x) = f(x+1) - 2*(fx) + f(x-1)$$

Cela permet d'avoir un masque simple (ici, l'inverse du laplacien):
$$\begin{pmatrix} -1 & 2 & -1\end{pmatrix}$$

Qui ne fonctionne que dans un sens (*et donc à appliquer à l'horizontal et vertical*).

Voici un masque calculant les deux dérivées partielles
$$
\begin{pmatrix}
0 & -1 & 0\\
-1 & 4 & -1\\
0 & -1 & 0
\end{pmatrix}
$$

:::warning
Le prof déconseille pour la détection de bord pure (mais à d'autres applications).
:::

#### Renforcement des contours (amélioration de la netteté)

On applique l'inverse du laplacien et on somme au signal d'origine. Donc partout on a un contour on étire les niveaux de gris juste avant et après:
$$
\begin{pmatrix}
0 & -1 & 0\\
-1 & 5 & -1\\
0 & -1 & 0
\end{pmatrix}
$$

On peut moduler l'amplitude de la netteté en multipliant le laplacien par un facteur arbitraire $$k$$.

#### Détection de coin


Si on a un coin, la dérivée serait forte dans deux directions, contrairement au point de contour.

**Filtre de Moravec**: on prend le minimum de la détection de contour dans les deux directions. Si le minimum est faible, ce n'est pas un coin.

**Filtre de Harris**: très coûteux. Super génial sur le papier mais dans la pratique très "capricieux".

**Filtre de Achard**: plus robuste que Harris, à priori

## Signaux

> Cf MASI et CODO

Savoir qu'un signal soit à support **borné** amène à des simplifications en image.

++Signaux classiques:++
* Porte
* Echelon d'Heavyside
* Signe
* Triangulaire
* Gaussienne
* Sinus cardinal
* Impulsion (pic de dirac)

:::warning
Relation TF **porte** $\rightarrow$ **sinus cardinal**
:::

On pourra choisir---selon la transformation souhaitée---la représentation la plus adaptée entre la représentation temporelle et fréquentielle (Parseval).

### Convolution

On peut décrire un filtre par sa réponse impulsionnelle à un pic de Dirac.

Propriétés :
* Commutativité
* Distributivité
* Associativité

**Théorème de Plancherel:** ("qui est super, super important")

Equivalence Convolution temporelle $\Longleftrightarrow$ Multiplication fréquentielle
**et**
Equivalence Convolution fréquentielle $\Longleftrightarrow$ Multiplication temporelle

Autre propriété:
$f \circledast g' = f'\circledast g = (f \circledast g)'$

Filtres typiques:
* Passe Bas
* Passe Haut

[Papier de Jonathan sur le recadrage de documents](https://projet.liris.cnrs.fr/imagine/pub/proceedings/ICIP-2014/Papers/1569913165.pdf)

### Autres transformées

* Short Term Fourier Transform:
On effectue une transformée **locale** (en multipliant la TF par une porte). Volonté d'avoir une information spatiale en plus de la fréquentielle.
$\rightarrow$ Capacité à analyser les **hautes fréquences** mais difficile pour les **basses** (régler la taille de l'échantillon)

* Tranformée en ondelettes

## Bruit

[Slides](http://jo.fabrizio.free.fr/teaching/ti/tifo_noise.pdf)

**Modèle de dégradation**
On considère que le signal a été *dégradé* par un autre convolué

$I_{deg} = h * I_{orig} + n$

avec $h := \text{dégradation (optique, flou)}$
et $n := \text{bruit (additif)}$

:::info
Appareil photos possèdent déjà des procédés d'**élimination de bruit** intégrés.
Ils sont facilités par la connaissance du matériel, et donc du type de bruit présent
:::

++Réduction du bruit:++
Tout un tas de **moyennes** pour atténuer le $n$ (on va privilégier le *gaussien séléctif*)

* Approche par **ondelettes** : on calcule un certain nombre d'itérations des ondelettes, jusqu'à trouver les très hautes fréquences (représentatives du bruit), puis on les soustrait à l'image
* **NLMeans** (Non-Local Means Denoising): on ne fait pas la moyenne sur un voisinage. Pour un patch considéré, on cherche d'autres patchs ressemblants, qui contribueront davantage dans la moyenne.
* Analyse du spectre fréquentiel $\rightarrow$ On peut filtrer certaines hautes fréquences en fonction de l'image

++Estimation du bruit:++
* Si le capteur est connu:
$\hookrightarrow$ On trouve repère en prenant en photo une zone homogène dans de bonnes conditions d'éclairement
* Si le capteur n'est **pas** connu
$\hookrightarrow$ On analyse différentes

++Réduction des dégradations convolutionnelles:++
On veut réduire la composante $h$ du bruit

* Blind deconvolution: on connaît seulement $I_{deg}$
* Non-Blind deconvolution : on connaît $I_{deg}$ et $h$ (même si on connaît $h$ c'est pas gagné!)

Si on a comme dégradation:
$g = h*f + n$
$TF \Rightarrow G(u, v) = H(u, v)F(u, v) + N(u, v)$

Si on suppose que $g = h*f$, c'est facile:

$Fe(u, v) = G(u, v) / H(u, v)$

Mais la composante en $N$ nous embête:
$F(u, v) = F(u, v) + \frac{N(u, v)}{H(u, v)} \rightarrow \text{composante non triviale}$

:::warning
++Attention:++ Ne pas travailler pour la mafia, la déconvolution ne marche pas à tous les coups, certains bruits sont prépondérants et ne peuvent pas être éliminés (vous si).
:::

* Filtre de Wiener: on cherche une estimation d'une image dont on connaît **tous les paramètres**

On cherche $W$ tel que $Fe = WG$

On a: $W = [\frac{H^2}{|H^2| + \frac{|N|^2}{|F|^2}}]$

On remarque qu'il faut connaitre $N$ et $F$, donc connaître la solution au problème lol. Néanmoins, on peut supposer le ratio constant et essayer de l'approcher.

$\hookrightarrow$ Difficile de déterminer $H$

## Implémentation

[Slides](http://jo.fabrizio.free.fr/teaching/ti/tifo_implementation.pdf)