I. How AES works

1. Keyed Permutations

Description (Translated)

• AES, tương tự như các loại mã hóa khối mạnh khác, đều thực hiện việc hoán vị khóa (keyed permutation).

Một block hay một khối trong mã hóa khối chính là một lượng cố định bits hay bytes của dữ liệu. AES nhận một khối làm input và mã hóa thành một khối khác trả ra output. CryptoHack sẽ cung cấp thông tin chính về loại mã hóa AES trên khối 128 bit (16 byte) và khóa 128 bit, hay được biết tới với tên gọi AES-128

• Sử dụng cùng một khóa, ta có thể thực hiện việc khôi phục lại bản rõ bằng cách sử dụng hoán vị ngược (inverse permutation). Điều này đặc biệt quan trọng bởi khóa chính là cầu nối (ánh xạ) giữa bản rõ và bản mã trong hệ mật đối xứng như AES, nếu không có khóa, việc giải mã sẽ rất khó khăn, gần như là không thể. Ánh xạ (Bijection) trong đại số là phép liên kết tương ứng mỗi phần tử x với một và chỉ một phần tử y của hai tập hợp.
• Câu hỏi: Thuật ngữ toán học nào có nghĩa là one-to-one correspondence.

Flag

crypto{bijection}

---

2. Resisting Bruteforce

Description (Translated)

• Với một mã khối đủ mạnh, một attacker sẽ không thể phân biệt bản mã của AES với một chuỗi bit được hoán vị ngẫu nhiên. Vì vậy, không có cách nào đơn giản hơn tấn công vét cạn tất cả các khóa có thể.

Xét việc tấn công vét cạn một khóa 128 bit của AES, có ước tính cho rằng sẽ mất tới hàng nghìn năm tuổi vũ trụ để phá khóa.

• Có một cách tấn công AES mạnh hơn vét cạn, trên thực tế nó chỉ làm giảm độ bảo mật của AES-128 xuống còn 126.1 bits. Đó chính là Biclique attack, là single-key attack tốt nhất từng được công bố nhưng không phải là một đe dọa quá lớn tới AES.
• Bên cạnh đó, máy tính lượng tử mặc dù có tiềm năng to lớn trong việc phá vỡ những hệ khóa công khai như RSA bằng Shor's algorithm, nó vẫn tương đối yếu khi chỉ có khả năng làm giảm độ bảo mật của AES xuống còn phân nửa bằng Grover's algorithm. Vì vậy người ta ưa dùng AES-256 hơn, dù khó để cài đặt hơn, bởi khả năng bảo mật mạnh mẽ trước máy tính lượng tử trong tương lai.
• Câu hỏi: Đâu là phương thức single-key attack on AES tốt nhất.

Flag

crypto{biclique}

---

3. Structure of AES

Description (Translated)

• Để tạo ra một khóa hoán vị đủ mạnh, AES kết hợp thực hiện nhiều phép biến đổi trên input. Đây là điểm tương phản với phương pháp của hệ mật RSA sử dụng những phép toán tinh tế, AES nhanh gọn và đơn giản hơn.
• AES-128 bắt đầu với một quy trình chính (key schedule) và thực hiện 10 vòng mỗi state. Ở đây, state khởi tạo chính là khối bản rõ được viết dưới dạng ma trận 4x4 bytes (4*4*8 = 128 bits).Trong mỗi 10 vòng, state sẽ được biến đổi bằng những thuật toán không thể đảo ngược.

Mỗi lần biến đổi đều tuân theo lý thuyết của Claude Shannon.

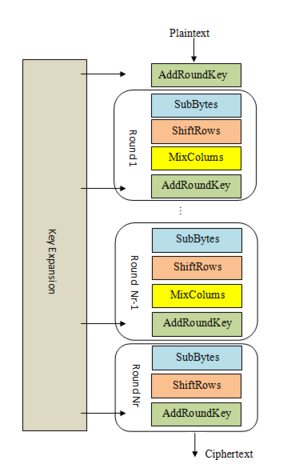
• Dưới đây là tổng quan các giai đoạn mã hóa AES:
  1. Mở rộng khóa: Từ khóa 128 bit, 11 khóa vòng 128 bit khác nhau được khởi tạo để sử dụng cho bước sau.
  2. Khởi tạo khóa: AddRoundKey: mỗi bytes của vòng đầu tiên sẽ được xor với bytes của state.
  3. Thuật toán: Thuật toán được lặp lại 10 lần, 9 lần lặp chính và một lần lặp cuối cùng gọi là final round:
  a. SubBytes: mỗi bytes của state được thay thês bằng một bytes khác bằng cách đối chiếu với S-box.
  b. ShiftRows: mỗi 3 hàng ma trận của state sẽ được chuyển vị trên một, hai hoặc ba cột.
  c. MixColumns: thực hiện phép nhân ma trận trên các cột của state, kết hợp với 4 bytes ở mỗi cột. MixColumns chỉ được thực hiện trên 9 vòng lặp đầu tiên.
  d. AddRoundKey: mỗi bytes của vòng đầu tiên sẽ được xor với bytes của trạng thái.
  
• Câu hỏi: Ta có hàm bytes2matrix giúp chuyển bản rõ dạng khối ban đầu thành một ma trận trạng thái. Viết hàm matrix2bytes để khôi phục lại bản rõ (chính là flag của bài)
• Challenge code:

def bytes2matrix(text):
    """ Converts a 16-byte array into a 4x4 matrix.  """
    return [list(text[i:i+4]) for i in range(0, len(text), 4)]

def matrix2bytes(matrix):
    """ Converts a 4x4 matrix into a 16-byte array.  """
    ????

matrix = [
    [99, 114, 121, 112],
    [116, 111, 123, 105],
    [110, 109, 97, 116],
    [114, 105, 120, 125],
]

print(matrix2bytes(matrix))

Solution

• Code:

def matrix2bytes(matrix):
    pt = b''
    for i in range(len(matrix)):
        for j in range(len(matrix[i])):
            pt += chr(matrix[i][j]).encode()
    return pt
matrix = [
    [99, 114, 121, 112],
    [116, 111, 123, 105],
    [110, 109, 97, 116],
    [114, 105, 120, 125],
]

print(matrix2bytes(matrix).decode())

Flag

crypto{inmatrix}

Note

• Thay vì code dài dòng như trên, ta có thể sử dụng hàm bytes và sum như sau:

def matrix2bytes(matrix):
    return bytes(sum(matrix, []))

---

4. Round Keys

Description (Translated)

• Sau bước khởi tạo khóa ở trên, AddRoundKey được thực hiện, nó xor state hiện tại với khóa vòng tương ứng.
  
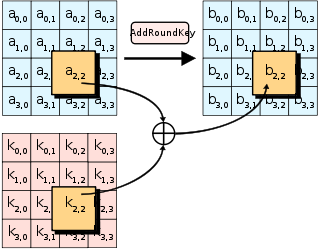
• AddRoundKey cũng được thực hiện ở cuối mỗi vòng. AddRoundKey cũng chính là giai đoạn duy nhất của AES mà khóa được trộn với state, tạo thành sự hoán vị khóa đặc biệt.
• Câu hỏi: viết hàm add_round_key và sử dụng hàm matrix2bytes để khôi phục lại flag.
• Challenge code:

state = [
    [206, 243, 61, 34],
    [171, 11, 93, 31],
    [16, 200, 91, 108],
    [150, 3, 194, 51],
]

round_key = [
    [173, 129, 68, 82],
    [223, 100, 38, 109],
    [32, 189, 53, 8],
    [253, 48, 187, 78],
]


def add_round_key(s, k):
    ???


print(add_round_key(state, round_key))

Solution

• Code:

from pwn import xor

state = [
    [206, 243, 61, 34],
    [171, 11, 93, 31],
    [16, 200, 91, 108],
    [150, 3, 194, 51],
]

round_key = [
    [173, 129, 68, 82],
    [223, 100, 38, 109],
    [32, 189, 53, 8],
    [253, 48, 187, 78],
]

def add_round_key(s, k):
    state = bytes(sum(s, []))
    key = bytes(sum(k, []))
    pt = b''
    for i in range(len(state)):
        pt += xor(state[i], key[i])
    return pt

print(add_round_key(state, round_key).decode())

Flag

crypto{r0undk3y}

Note

• Thực ra ta có thể viết hàm add_round_key bằng chỉ một dòng như sau:

def add_round_key(s, k):
    return xor(s, k)

---

5. Confusion through Substitution

Description (Translated)

• Bước đầu tiên của mỗi vòng AES là SubBytes. Ta lấy mỗi bytes của ma trận state và thay thế chúng với một byte khác trong bảng tra 16x16 gọi là S-box.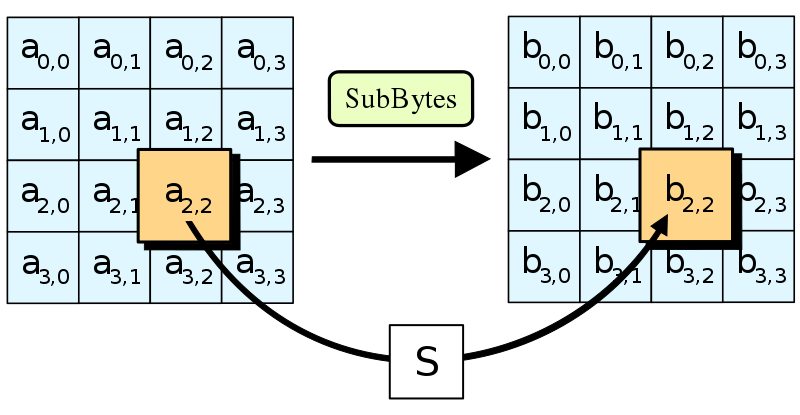
  
• Từ "confusion" bắt nguồn từ lý thuyết của nhà toán học Claude Shannon năm 1945, đề cập tới mối liên hệ giữa bản mã và khóa nên được phức tạp hóa hết mức có thể. Sao cho khi chỉ có bản mã, không một ai có thể biết điều gì về khóa. Nếu một mật mã có "confusion" yếu, nó sẽ dễ bị phá vỡ hơn.
• Mục đích chính của việc xây dụng S-box là để tạo ra bản mã khó bị phân tích bởi các hàm tuyến tính.
• Câu hỏi: viết hàm sub_bytes và truyền dữ liệu một ma trận state qua một S-box đảo ngược và khôi phục flag.
• Challenge code:

s_box = (
    0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
    0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
    0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
    0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
    0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
    0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
    0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
    0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
    0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
    0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
    0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
    0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
    0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
    0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
    0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
    0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16,
)

inv_s_box = (
    0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB,
    0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB,
    0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E,
    0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25,
    0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92,
    0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84,
    0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06,
    0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B,
    0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73,
    0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E,
    0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B,
    0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4,
    0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F,
    0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF,
    0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61,
    0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D,
)

state = [
    [251, 64, 182, 81],
    [146, 168, 33, 80],
    [199, 159, 195, 24],
    [64, 80, 182, 255],
]


def sub_bytes(s, sbox=s_box):
    ???


print(sub_bytes(state, sbox=inv_s_box))

Solution

• Ta chỉ cần truyền ma trận state vào inv_s_box là xong.
• Code:

s_box = (
    0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
    0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
    0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
    0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
    0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
    0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
    0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
    0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
    0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
    0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
    0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
    0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
    0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
    0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
    0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
    0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16,
)

inv_s_box = (
    0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB,
    0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB,
    0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E,
    0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25,
    0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92,
    0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84,
    0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06,
    0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B,
    0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73,
    0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E,
    0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B,
    0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4,
    0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F,
    0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF,
    0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61,
    0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D,
)

state = [
    [251, 64, 182, 81],
    [146, 168, 33, 80],
    [199, 159, 195, 24],
    [64, 80, 182, 255],
]


def sub_bytes(s, sbox=s_box):
    s = sum(s, [])
    for i in range(len(s)):
        s[i] = sbox[s[i]]
    return bytes(s)

print(sub_bytes(state, sbox=inv_s_box).decode())

Flag

crypto{l1n34rly}

---

6. Diffusion through Permutation

Description (Translated)

• Ta đã thấy được cách mà S-box tạo ra tính "confusion" cho AES. Một tính chất khác mà trong lý thuyết của Shannon cũng được đề cập là "diffusion", nghĩa là cách mà bản rõ khuếch tán đến bản mã.
• Bản thân việc SubBytes các bytes đã tạo ra sự phi tuyến tính cho hệ mật AES, tuy nhiên nó không phân phối trên toàn state. Nếu không có "diffusion", các bytes giống nhau ở cùng một vị trí sẽ có cách SubBytes y hệt nhau, điều này làm giảm tính bảo mật của AES bởi attacker có thể tấn công từng bytes riêng lẻ trong ma trận state. Chính vì vậy, ta cần xáo trộn ma trận trạng thái (tất nhiên là có thể khôi phục lại). Mỗi đầu vào của S-box kế tiếp sẽ trở thành hàm của rất nhiều bytes khác nhau, làm tăng đáng kể tính phức tạp của AES.

Một "diffusion" lí tưởng có thể khiến sự thay đổi một bit trong bản rõ làm ảnh hưởng tới nửa số bits của bản mã. Đây chính là Avalanche effect.

• Bước ShiftRows và MixColumns kết hợp với nhau để tạo ra "diffusion" này, đảm bảo rằng mỗi byte sẽ ảnh hưởng tới các bytes khác trong state chỉ với 2 vòng tạo mã.
• ShiftRows là cách biến đổi đơn giản nhất trong AES. Cách thực hiện có thể thấy qua hình sau:
  
  
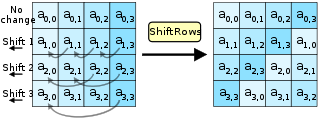
• MixColumns phức tạp hơn bởi nó thực hiện việc nhân ma trận giữa cột của ma trận state và một ma trận cho trước trong trường Galois. Vì thế mỗi bytes của cột ảnh hưởng tới toàn bộ bytes trong cột kết quả. Tham khảo tại đây, wikipedia này và hình sau:
  
  
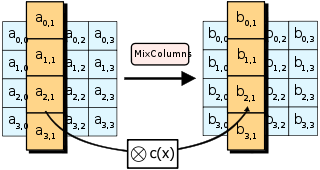
• Câu hỏi: Cho biết code để thực hiện MixColumns và ShiftRows, khôi phục flag.
• Challenge code:

def shift_rows(s):
    s[0][1], s[1][1], s[2][1], s[3][1] = s[1][1], s[2][1], s[3][1], s[0][1]
    s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
    s[0][3], s[1][3], s[2][3], s[3][3] = s[3][3], s[0][3], s[1][3], s[2][3]


def inv_shift_rows(s):
    ???


# learned from http://cs.ucsb.edu/~koc/cs178/projects/JT/aes.c
xtime = lambda a: (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1)


def mix_single_column(a):
    # see Sec 4.1.2 in The Design of Rijndael
    t = a[0] ^ a[1] ^ a[2] ^ a[3]
    u = a[0]
    a[0] ^= t ^ xtime(a[0] ^ a[1])
    a[1] ^= t ^ xtime(a[1] ^ a[2])
    a[2] ^= t ^ xtime(a[2] ^ a[3])
    a[3] ^= t ^ xtime(a[3] ^ u)


def mix_columns(s):
    for i in range(4):
        mix_single_column(s[i])


def inv_mix_columns(s):
    # see Sec 4.1.3 in The Design of Rijndael
    for i in range(4):
        u = xtime(xtime(s[i][0] ^ s[i][2]))
        v = xtime(xtime(s[i][1] ^ s[i][3]))
        s[i][0] ^= u
        s[i][1] ^= v
        s[i][2] ^= u
        s[i][3] ^= v

    mix_columns(s)


state = [
    [108, 106, 71, 86],
    [96, 62, 38, 72],
    [42, 184, 92, 209],
    [94, 79, 8, 54],
]

Solution

• Nhìn vào hàm shift_rows khá đơn giản ở kia, ta có thể viết hàm inv_shift_rows như sau (nên kiểm tra lại):

def inv_shift_rows(s):
    s[3][3], s[0][3], s[1][3], s[2][3] = s[0][3], s[1][3], s[2][3], s[3][3]
    s[2][2], s[3][2], s[0][2], s[1][2] = s[0][2], s[1][2], s[2][2], s[3][2]
    s[1][1], s[2][1], s[3][1], s[0][1] = s[0][1], s[1][1], s[2][1], s[3][1]

• Sau đó sử dụng mix_columns rồi inv_shift_rows, ta có được flag:

inv_mix_columns(state)
inv_shift_rows(state)
print(bytes(sum(state, [])).decode())

Flag

crypto{d1ffUs3R}

Note

• Có một cách viết hàm inv_shift_rows ngắn hơn, đó chính là thực hiện shift rows 3 lần. Ma trận có dạng 4x4 nên nếu dịch chuyển đủ 4 lần, ma trận sẽ được khôi phục lại như ban đầu. Vì vậy ta viết như sau:

def inv_shift_rows(s):
    for i in range(3):
        shift_rows(s)

---

7. Bringing It All Together

Description

• Challenge code:

N_ROUNDS = 10

key        = b'\xc3,\\\xa6\xb5\x80^\x0c\xdb\x8d\xa5z*\xb6\xfe\\'
ciphertext = b'\xd1O\x14j\xa4+O\xb6\xa1\xc4\x08B)\x8f\x12\xdd'



def expand_key(master_key):
    """
    Expands and returns a list of key matrices for the given master_key.
    """

    # Round constants https://en.wikipedia.org/wiki/AES_key_schedule#Round_constants
    r_con = (
        0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40,
        0x80, 0x1B, 0x36, 0x6C, 0xD8, 0xAB, 0x4D, 0x9A,
        0x2F, 0x5E, 0xBC, 0x63, 0xC6, 0x97, 0x35, 0x6A,
        0xD4, 0xB3, 0x7D, 0xFA, 0xEF, 0xC5, 0x91, 0x39,
    )

    # Initialize round keys with raw key material.
    key_columns = bytes2matrix(master_key)
    iteration_size = len(master_key) // 4

    # Each iteration has exactly as many columns as the key material.
    i = 1
    while len(key_columns) < (N_ROUNDS + 1) * 4:
        # Copy previous word.
        word = list(key_columns[-1])

        # Perform schedule_core once every "row".
        if len(key_columns) % iteration_size == 0:
            # Circular shift.
            word.append(word.pop(0))
            # Map to S-BOX.
            word = [s_box[b] for b in word]
            # XOR with first byte of R-CON, since the others bytes of R-CON are 0.
            word[0] ^= r_con[i]
            i += 1
        elif len(master_key) == 32 and len(key_columns) % iteration_size == 4:
            # Run word through S-box in the fourth iteration when using a
            # 256-bit key.
            word = [s_box[b] for b in word]

        # XOR with equivalent word from previous iteration.
        word = bytes(i^j for i, j in zip(word, key_columns[-iteration_size]))
        key_columns.append(word)

    # Group key words in 4x4 byte matrices.
    return [key_columns[4*i : 4*(i+1)] for i in range(len(key_columns) // 4)]


def decrypt(key, ciphertext):
    round_keys = expand_key(key) # Remember to start from the last round key and work backwards through them when decrypting

    # Convert ciphertext to state matrix

    # Initial add round key step

    for i in range(N_ROUNDS - 1, 0, -1):
        pass # Do round

    # Run final round (skips the InvMixColumns step)

    # Convert state matrix to plaintext

    return plaintext

# print(decrypt(key, ciphertext))

Solution

• Dựa theo gợi ý của bài, ta sẽ thực hiện việc giải mã theo chiều mũi tên:
  
  
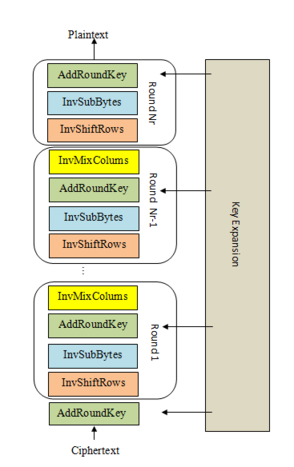
• Code (hơi dài nên thay vì viết từng hàm ra ta có thể sử dụng code từ những bài trên bằng syntax from ... import):

from pwn import xor

s_box = (
    0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
    0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
    0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
    0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
    0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
    0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
    0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
    0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
    0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
    0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
    0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
    0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
    0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
    0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
    0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
    0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16,
)
inv_s_box = (
    0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB,
    0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB,
    0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E,
    0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25,
    0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92,
    0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84,
    0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06,
    0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B,
    0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73,
    0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E,
    0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B,
    0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4,
    0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F,
    0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF,
    0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61,
    0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D,
)
def inv_shift_rows(s):
    s[0][1], s[1][1], s[2][1], s[3][1] = s[3][1], s[0][1], s[1][1], s[2][1]
    s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
    s[0][3], s[1][3], s[2][3], s[3][3] = s[1][3], s[2][3], s[3][3], s[0][3]

def add_round_key(s, k):
    return bytes2matrix(xor(s, k))

def bytes2matrix(text):
    return [list(text[i:i+4]) for i in range(0, len(text), 4)]
def matrix2bytes(matrix):
    return bytes(sum(matrix, []))
xtime = lambda a: (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1)

def mix_single_column(a):
    t = a[0] ^ a[1] ^ a[2] ^ a[3]
    u = a[0]
    a[0] ^= t ^ xtime(a[0] ^ a[1])
    a[1] ^= t ^ xtime(a[1] ^ a[2])
    a[2] ^= t ^ xtime(a[2] ^ a[3])
    a[3] ^= t ^ xtime(a[3] ^ u)
def mix_columns(s):
    for i in range(4):
        mix_single_column(s[i])
def inv_mix_columns(s):
    for i in range(4):
        u = xtime(xtime(s[i][0] ^ s[i][2]))
        v = xtime(xtime(s[i][1] ^ s[i][3]))
        s[i][0] ^= u
        s[i][1] ^= v
        s[i][2] ^= u
        s[i][3] ^= v

    mix_columns(s)

def sub_bytes(s, sbox=s_box):
    s = sum(s, [])
    for i in range(len(s)):
        s[i] = sbox[s[i]]
    return bytes(s)
def inv_sub_bytes(s, sbox=inv_s_box):
    return sub_bytes(s, sbox=inv_s_box)

def expand_key(master_key):
    r_con = (
        0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40,
        0x80, 0x1B, 0x36, 0x6C, 0xD8, 0xAB, 0x4D, 0x9A,
        0x2F, 0x5E, 0xBC, 0x63, 0xC6, 0x97, 0x35, 0x6A,
        0xD4, 0xB3, 0x7D, 0xFA, 0xEF, 0xC5, 0x91, 0x39,
    )
    key_columns = bytes2matrix(master_key)
    iteration_size = len(master_key) // 4
    i = 1
    while len(key_columns) < (N_ROUNDS + 1) * 4:
        word = list(key_columns[-1])
        if len(key_columns) % iteration_size == 0:
            word.append(word.pop(0))
            word = [s_box[b] for b in word]
            word[0] ^= r_con[i]
            i += 1
        elif len(master_key) == 32 and len(key_columns) % iteration_size == 4:
            word = [s_box[b] for b in word]
        word = bytes(i^j for i, j in zip(word, key_columns[-iteration_size]))
        key_columns.append(word)

    return [key_columns[4*i : 4*(i+1)] for i in range(len(key_columns) // 4)]

def decrypt(key, ciphertext):
    round_keys = expand_key(key) # Remember to start from the last round key and work backwards through them when decrypting
    state = bytes2matrix(ciphertext)
    state = add_round_key(state, round_keys[10])
    for i in range(N_ROUNDS - 1, 0, -1):
        inv_shift_rows(state)
        state = inv_sub_bytes(state)
        state = add_round_key(state, round_keys[i])
        inv_mix_columns(state)

    inv_shift_rows(state)
    state = inv_sub_bytes(state)
    state = add_round_key(state, round_keys[0])
    plaintext = matrix2bytes(state)
    return plaintext

N_ROUNDS = 10
key        = b'\xc3,\\\xa6\xb5\x80^\x0c\xdb\x8d\xa5z*\xb6\xfe\\'
ciphertext = b'\xd1O\x14j\xa4+O\xb6\xa1\xc4\x08B)\x8f\x12\xdd'

print(decrypt(key, ciphertext).decode())

Flag:

crypto{MYAES128}

Note:

• Giải xong bài thấy buồn thiu vì bài này hay vãi nho

---

II. SYMMETRIC STARTER

8. Modes of Operation Starter

Description (Translated)

• Phần I đã giới thiệu chi tiết về việc hoán vị khóa của AES. Trên thực tế, ta cần mã hóa tin nhắn dài hơn một khối. Chính vì vậy, các "mode of operation" ra đời để thực hiện việc mã hóa AES trên một tin nhắn dài.
• Tất cả các modes đều có những nhược điểm nhất định khi không được cài đặt đúng cách. Challenge của bài giới thiệu một website để tương tác với APIs và khai thác một vài lỗ hổng trong mode ECB.
• Challenge code:

from Crypto.Cipher import AES


KEY = ?
FLAG = ?


@chal.route('/block_cipher_starter/decrypt/<ciphertext>/')
def decrypt(ciphertext):
    ciphertext = bytes.fromhex(ciphertext)

    cipher = AES.new(KEY, AES.MODE_ECB)
    try:
        decrypted = cipher.decrypt(ciphertext)
    except ValueError as e:
        return {"error": str(e)}

    return {"plaintext": decrypted.hex()}


@chal.route('/block_cipher_starter/encrypt_flag/')
def encrypt_flag():
    cipher = AES.new(KEY, AES.MODE_ECB)
    encrypted = cipher.encrypt(FLAG.encode())

    return {"ciphertext": encrypted.hex()}

Solution

• Ta chỉ cần đưa ciphertext ở Encrypt_Flag vào hàm decrypt có sẵn để nhận được plaintext. Đem đi dịch qua hex ta nhận được flag. Với bài này, ta không cần biết key để giải mã vì key được tái sử dụng trong chính hàm decrypt rồi.
• Code:

from requests import get
from json import loads

def decrypt(ct):
    url = f'https://aes.cryptohack.org/block_cipher_starter/decrypt/{ct}/'
    r = get(url)
    pt = (loads(r.text))['plaintext']
    return bytes.fromhex(pt).decode()

def encrypt_flag():
    url = 'https://aes.cryptohack.org/block_cipher_starter/encrypt_flag/'
    r = get(url)
    ct = (loads(r.text))['ciphertext']
    return ct

flag = decrypt(encrypt_flag())
print(flag)

Flag

crypto{bl0ck_c1ph3r5_4r3_f457_!}

---

9. Passwords as Keys

Description (Translated)

• Trong AES, hiển nhiên khóa là một chuỗi các bytes ngẫu nhiên thay vì mật khẩu hay những loại dữ liệu dễ đoán khác. Khóa có thể được tạo ra bằng CSPRNG (hay cryptographically-secure pseudorandom number generator).
• Khóa trông giống một chuỗi bytes ngẫu nhiên, tuy nhiên không nhất thiết phải như vậy. Trong trường hợp này khóa được tạo ra từ mật khẩu đơn giản sử dụng hàm băm.
• Website để tìm flag
• Challenge code:

from Crypto.Cipher import AES
import hashlib
import random


# /usr/share/dict/words from
# https://gist.githubusercontent.com/wchargin/8927565/raw/d9783627c731268fb2935a731a618aa8e95cf465/words
with open("/usr/share/dict/words") as f:
    words = [w.strip() for w in f.readlines()]
keyword = random.choice(words)

KEY = hashlib.md5(keyword.encode()).digest()
FLAG = ?


@chal.route('/passwords_as_keys/decrypt/<ciphertext>/<password_hash>/')
def decrypt(ciphertext, password_hash):
    ciphertext = bytes.fromhex(ciphertext)
    key = bytes.fromhex(password_hash)

    cipher = AES.new(key, AES.MODE_ECB)
    try:
        decrypted = cipher.decrypt(ciphertext)
    except ValueError as e:
        return {"error": str(e)}

    return {"plaintext": decrypted.hex()}


@chal.route('/passwords_as_keys/encrypt_flag/')
def encrypt_flag():
    cipher = AES.new(KEY, AES.MODE_ECB)
    encrypted = cipher.encrypt(FLAG.encode())

    return {"ciphertext": encrypted.hex()}

Solution

• Hướng đi của bài là brute-force, key là bluebell sau khi chạy xong vòng lặp.
• Code:

from requests import get
from json import loads
from hashlib import md5
from Crypto.Cipher import AES

def encrypt_flag():
    url = 'https://aes.cryptohack.org/passwords_as_keys/encrypt_flag/'
    r = get(url)
    ct = (loads(r.text))['ciphertext']
    return bytes.fromhex(ct)

gist = 'https://gist.githubusercontent.com/wchargin/8927565/raw/d9783627c731268fb2935a731a618aa8e95cf465/words'
keys = get(gist).text.split("\n")
ct = encrypt_flag()

for key in keys:
    key = md5(key.encode()).digest()
    cipher = AES.new(key, AES.MODE_ECB)
    flag = cipher.decrypt(ct)
    if(b'crypto' in flag):
        print(flag.decode())
        break

Flag

crypto{k3y5__r__n07__p455w0rdz?}

Note

• Đừng gửi brute force từng key lên web nếu không muốn nổ máy

---

III. BLOCK CIPHERS

10. ECB CBC WTF

Description

• Here you can encrypt in CBC but only decrypt in ECB. That shouldn't be a weakness because they're different modes… right?
• Play here
• Challenge code:

from Crypto.Cipher import AES


KEY = ?
FLAG = ?


@chal.route('/ecbcbcwtf/decrypt/<ciphertext>/')
def decrypt(ciphertext):
    ciphertext = bytes.fromhex(ciphertext)

    cipher = AES.new(KEY, AES.MODE_ECB)
    try:
        decrypted = cipher.decrypt(ciphertext)
    except ValueError as e:
        return {"error": str(e)}

    return {"plaintext": decrypted.hex()}


@chal.route('/ecbcbcwtf/encrypt_flag/')
def encrypt_flag():
    iv = os.urandom(16)

    cipher = AES.new(KEY, AES.MODE_CBC, iv)
    encrypted = cipher.encrypt(FLAG.encode())
    ciphertext = iv.hex() + encrypted.hex()

    return {"ciphertext": ciphertext}

Solution

• Mode CBC:
  
  
• Đầu tiên, ta lấy giá trị của ciphertext. Trước tiên ta cần chuyển ciphertext thành dạng bytes. Nhận thấy ciphertext có độ dài 48, trong đó iv là 16 kí tự đầu nên ta sẽ chia đoạn bản mã sau thành hai block1 và block2.
• Ý tưởng giải mã khá đơn giản nếu nhìn vào sơ đồ giải mã CBC ở trên. Với iv ta đã có, bên cạnh đó web còn cung cấp một hàm giải mã bằng ECB (hàm này giúp ta bypass việc thiếu key). Code của chúng ta sẽ như sau (code làm gián tiếp chứ không tương tác trực tiếp với web):

from pwn import xor

ct = '46114097100b0e0fbdc0f0c3cb530ed403091e84ead0642081f1773557a176484bb32e1da722966127bc7f6868894dd6'
ct = bytes.fromhex(ct)
iv = ct[:16]
block1 = ct[16:32]
block2 = ct[32:]
print(bytes.hex(block1), bytes.hex(block2), sep='\n\n')

# Sau khi đem đi decrypt block1 và block2 trên web ta được pt1 và pt2
pt1 = '256339e76464753cdea2aff6be3065e1'
pt2 = '5c3d68b4dbb43b11b6ae561476805735'
pt1 = xor(bytes.fromhex(pt1), iv)
pt2 = xor(bytes.fromhex(pt2), block1)
print(pt1.decode(), pt2.decode(), sep='')

Flag

crypto{3cb_5uck5_4v01d_17_!!!}

Note

• Một bài khá hay giúp hiểu rõ hơn về hai mode được sử dụng nhiều là ECB và CBC. Bên cạnh đó ta có code để tương tác trực tiếp với web như sau:

from pwn import *
import requests
from json import loads

def decrypt(ct):
	ct = bytes.hex(ct)
	url = f"http://aes.cryptohack.org/ecbcbcwtf/decrypt/{ct}/"
	r = requests.get(url)
	dec = (loads(r.text))["plaintext"]
	return bytes.fromhex(dec)

def encrypt_flag():
	url = "http://aes.cryptohack.org/ecbcbcwtf/encrypt_flag/"
	r = requests.get(url)
	enc = (loads(r.text))["ciphertext"]
	return bytes.fromhex(enc)

enc = encrypt_flag()
iv = enc[:16]
block1 = enc[16:32]
block2 = enc[32:]

pt1 = xor(decrypt(block1), iv)
pt2 = xor(decrypt(block2), block1)
flag = (pt1 + pt2).decode()
print(flag)

---

11. ECB Oracle

Description

• ECB is the most simple mode, with each plaintext block encrypted entirely independently. In this case, your input is prepended to the secret flag and encrypted and that's it. We don't even provide a decrypt function. Perhaps you don't need a padding oracle when you have an "ECB oracle"?
• Play here
• Challenge code:

from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad


KEY = ?
FLAG = ?


@chal.route('/ecb_oracle/encrypt/<plaintext>/')
def encrypt(plaintext):
    plaintext = bytes.fromhex(plaintext)

    padded = pad(plaintext + FLAG.encode(), 16)
    cipher = AES.new(KEY, AES.MODE_ECB)
    try:
        encrypted = cipher.encrypt(padded)
    except ValueError as e:
        return {"error": str(e)}

    return {"ciphertext": encrypted.hex()}

Solution

• Trước tiên ta cần hiểu được cơ chế padding của code trên. Code sẽ tự động đệm thêm các bytes để độ dài block là một bội của 16, tại đây ta có thể xác định được độ dài của flag. Code như sau:

import requests
from pwn import *
from json import loads

def encrypt(pt):
    pt = bytes.hex(pt)
    url = f"https://aes.cryptohack.org/ecb_oracle/encrypt/{pt}/"
    r = requests.get(url)
    ct = (loads(r.text))['ciphertext']
    return ct

for i in range(1, 20):
    pt = b'\x00'*i
    get = bytes.fromhex(encrypt(pt))
    print(len(get), i)

• Chạy một code đơn giản như trên, ta nhận thấy với giá trị i = 6 thì len(get) = 32 , i = 7 thì len(get) = 48. Chính vì vậy, len(FLAG) thỏa mãn 7 + len(FLAG) = 32 nên len(FLAG) = 25. Cũng khá may mắn khi mode được chọn là ECB nên công việc đơn giản hơn rất nhiều. Bên cạnh đó ta có thể sử dụng len(FLAG) để assert sau.
• Trước khi đi vào giải bài toán, ta cần biết sơ đồ của ECB:
  
  
• Ta sẽ giải bài toán theo thuật toán này. Vì brute force khá lâu nên ta không chọn FLAG = '' mà là FLAG = 'crypto{'.
• Code:

import requests
from pwn import *
from json import loads

def encrypt(pt):
    pt = bytes.hex(pt)
    url = f"https://aes.cryptohack.org/ecb_oracle/encrypt/{pt}/"
    r = requests.get(url)
    ct = (loads(r.text))['ciphertext']
    return bytes.fromhex(ct)

LEN = 25
FLAG = 'crypto{'
chars = '0123456789abcdefghijklmnopqrstuvwxyz{_}'

for i in range(8, 26):
    num = 32 - i
    OFFSET = b'\x00' * num
    check1 = encrypt(OFFSET)[32-LEN:32]
    for char in chars:
        check2 = encrypt(OFFSET + (FLAG + char).encode())[32-LEN:32]
        if check1 == check2:
            FLAG += char
            print(FLAG)
            break 
assert len(FLAG) == LEN

Flag

crypto{p3n6u1n5_h473_3cb}

Note

• Đây là một bài khá hay cũng tựa tựa Padding Oracle Attack on CBC. Bạn mình trước cũng làm bài này nhưng đọc từ đuôi flag trở về đầu mà đến bây giờ mình vẫn không hiểu sao làm được thế .
• Lấy chars trong khoảng trên cho dễ, cũng may FLAG không troll bằng mấy kí tự quần què khác .

---

12. Flipping Cookie

Description

• You can get a cookie for my website, but it won't help you read the flag… I think.
• Play here
• Challenge code:

from Crypto.Cipher import AES
import os
from Crypto.Util.Padding import pad, unpad
from datetime import datetime, timedelta


KEY = ?
FLAG = ?


@chal.route('/flipping_cookie/check_admin/<cookie>/<iv>/')
def check_admin(cookie, iv):
    cookie = bytes.fromhex(cookie)
    iv = bytes.fromhex(iv)

    try:
        cipher = AES.new(KEY, AES.MODE_CBC, iv)
        decrypted = cipher.decrypt(cookie)
        unpadded = unpad(decrypted, 16)
    except ValueError as e:
        return {"error": str(e)}

    if b"admin=True" in unpadded.split(b";"):
        return {"flag": FLAG}
    else:
        return {"error": "Only admin can read the flag"}


@chal.route('/flipping_cookie/get_cookie/')
def get_cookie():
    expires_at = (datetime.today() + timedelta(days=1)).strftime("%s")
    cookie = f"admin=False;expiry={expires_at}".encode()

    iv = os.urandom(16)
    padded = pad(cookie, 16)
    cipher = AES.new(KEY, AES.MODE_CBC, iv)
    encrypted = cipher.encrypt(padded)
    ciphertext = iv.hex() + encrypted.hex()

    return {"cookie": ciphertext}

Solution

• Tham khảo tại link
• Chúng ta sẽ quan sát hàm get_cookie() trước. Hàm dùng để mã hóa cookie sau khi pad, với giá trị của iv gắn ở đầu. Ta có thể lấy giá trị cookie dễ dàng.
• Ta đã biết được mode CBC chia bản rõ thành các khối 16 bytes, vậy thì ở đây ta có khối đầu tiên là: block = admin=False;expi,… Quan sát tiếp hàm check_admin, hàm sẽ nhả flag khi thỏa mãn b"admin=True" in unpadded.split(b";"). Vì vậy, ta chỉ cần thay đổi admin=False thành admin=True là xong. Tuy nhiên để giữ được độ dài của block và thỏa mãn điều kiện, ta sẽ dùng fake_block = b'admin=True;expir' (thêm một bytes b'r') để bypass điều kiện padding.
• Bên cạnh đó, ta cũng cần tạo ra một fake_iv để bypass hàm unpad. Cụ thể như sau:

ct_block = E(key, xor(block, iv))
ct_fake = E(key, xor(fake_block, fake_iv))

D(ct_block, key) = xor(block, iv)
D(ct_fake, key) = xor(fake_block, fake_iv)

• Ta cần: ct_block = ct_fake

=> D(ct_block, key) = D(ct_fake, key)
=> xor(block, iv) = xor(fake_block, fake_iv)
=> fake_iv = xor(fake_block, block, iv)

• Khi có đủ hai giá trị cookie và fake_iv, ta có được flag.
• Code:

import requests
from json import loads
from pwn import xor

def check_admin(cookie, iv):
    cookie, iv = bytes.hex(cookie), bytes.hex(iv)
    url = f"https://aes.cryptohack.org/flipping_cookie/check_admin/{cookie}/{iv}/"
    r = requests.get(url)
    flag = loads(r.text)
    return flag

def get_cookie():
    url = "https://aes.cryptohack.org/flipping_cookie/get_cookie"
    r = requests.get(url)
    cookie = (loads(r.text))['cookie']
    cookie = bytes.fromhex(cookie)
    return cookie

temp = get_cookie()
iv, cookie = temp[:16], temp[16:]

block = b'admin=False;expi'
fake_block = b'admin=True;expir'
fake_iv = xor(fake_block, block, iv)

flag = check_admin(cookie, fake_iv)['flag']
print(flag)

Flag

crypto{4u7h3n71c4710n_15_3553n714l}

Note

• Một bài khá hay làm mình nhớ tới bài SHA256 Length Extension Attack trước giải ở CSTV .
• Trên CTFlearn cũng có một bài tương tự là We want Nudes instead of Nukes, code của bài như sau:

from pwn import xor

enc = '391e95a15847cfd95ecee8f7fe7efd66,8473dcb86bc12c6b6087619c00b6657e'
iv, c = enc.split(',')
iv, c = bytes.fromhex(iv), bytes.fromhex(c)

real = b'FIRE_NUKES_MELA!'
fake = b'SEND_NUDES_MELA!'
fake_iv = xor(real, fake, iv)
fake_iv, c = bytes.hex(fake_iv), bytes.hex(c)

flag = 'flag{' + fake_iv + ',' + c + '}'
print(flag)
'''
E(real ^ iv) = rc        E(fake ^ fake_iv) = fc
D(rc) ^ iv = real        D(fc) ^ fake_iv = fake
D(rc) = real ^ iv        D(fc) = fake ^ fake_iv

Cần rc = fc thì D(rc) = D(fc)
=> fake_iv = real ^ fake ^ iv
'''

---

13. Lazy CBC

Description

• I'm just a lazy dev and want my CBC encryption to work. What's all this talk about initialisations vectors? Doesn't sound important.
• Play here
• Challenge code:

from Crypto.Cipher import AES


KEY = ?
FLAG = ?


@chal.route('/lazy_cbc/encrypt/<plaintext>/')
def encrypt(plaintext):
    plaintext = bytes.fromhex(plaintext)
    if len(plaintext) % 16 != 0:
        return {"error": "Data length must be multiple of 16"}

    cipher = AES.new(KEY, AES.MODE_CBC, KEY)
    encrypted = cipher.encrypt(plaintext)

    return {"ciphertext": encrypted.hex()}


@chal.route('/lazy_cbc/get_flag/<key>/')
def get_flag(key):
    key = bytes.fromhex(key)

    if key == KEY:
        return {"plaintext": FLAG.encode().hex()}
    else:
        return {"error": "invalid key"}


@chal.route('/lazy_cbc/receive/<ciphertext>/')
def receive(ciphertext):
    ciphertext = bytes.fromhex(ciphertext)
    if len(ciphertext) % 16 != 0:
        return {"error": "Data length must be multiple of 16"}

    cipher = AES.new(KEY, AES.MODE_CBC, KEY)
    decrypted = cipher.decrypt(ciphertext)

    try:
        decrypted.decode() # ensure plaintext is valid ascii
    except UnicodeDecodeError:
        return {"error": "Invalid plaintext: " + decrypted.hex()}

    return {"success": "Your message has been received"}

Solution

• Trước hết, ta cần biết sơ đồ mã hóa của mode CBC như sau:

• Tổng quan công thức của chúng ta sẽ là: C = E(key, xor(P, key)). Vì vậy, nếu chọn P = b'\x00'*16, ta có thể rút gọn được thành C = E(key, key)
• Ta sẽ gửi hai bản rõ như sau:

pt1 = '0'*16
pt2 = '0'*32

• Khi đó, web sẽ trả về cho ta hai giá trị tương ứng:

ct1 = '8a187e5616873021da43e78e93f53514'
ct2 = '8a187e5616873021da43e78e93f535145c477e6f54632cd93d6ba5b87512ae5b'

• Tuy nhiên ta cần điều chỉnh lại một chút. Phần ct2 thực sự chính là ct2[len(ct1):], phần pt2 thực sự là pt2[len(pt1):]dựa vào sơ đồ giải mã ở trên. Tới đây, ta có các phép biến đổi:

pt1 = xor(D(key, ct1), key)
pt2 = xor(D(key, ct2), ct1)

D(key, ct1) = xor(pt1, key) # Tuy nhiên phần này trên web không trả về giá trị cho chúng ta
D(key, ct2) = xor(pt2, ct1) = temp # Phần này trả về plaintext bị lỗi, đó chính là key mã hóa

• Nhận được giá trị của temp, ta tính key = xor(temp, ct1) và submit trên web thu được flag dễ dàng.
• Code:

from pwn import *
import requests
from json import loads

def encrypt(pt):
    pt = bytes.hex(pt)
    url = f"http://aes.cryptohack.org/lazy_cbc/encrypt/{pt}/"
    r = requests.get(url)
    enc = (loads(r.text))['ciphertext']
    return enc

def receive(ct):
    url = f"http://aes.cryptohack.org/lazy_cbc/receive/{ct}/"
    r = requests.get(url)
    pt = loads(r.text)['error'].split(": ")[1]
    return pt

def get_flag(key):
    key = bytes.hex(key)
    url = f"http://aes.cryptohack.org/lazy_cbc/get_flag/{key}/"
    r = requests.get(url)
    flag = (loads(r.text))['plaintext']
    return flag

pt1 = b'\x00'*16
pt2 = b'\x00'*32
ct1, ct2 = encrypt(pt1), encrypt(pt2)
ct2 = ct2[len(ct1):]
temp = receive(ct2)
key = xor(bytes.fromhex(temp), bytes.fromhex(ct1))
flag = get_flag(key)
print(bytes.fromhex(flag).decode())

Flag

crypto{50m3_p30pl3_d0n7_7h1nk_IV_15_1mp0r74n7_?}

Note

• Nếu biến đổi trên khó hiểu có thể xem write up này (Bài này làm xong rùi em mới xem wu nha anh Tuệ )

---

14. Triple DES

Description

• Data Encryption Standard was the forerunner to AES, and is still widely used in some slow-moving areas like the Payment Card Industry. This challenge demonstrates a strange weakness of DES which a secure block cipher should not have.
• Play here
• Challenge code:

from Crypto.Cipher import DES3
from Crypto.Util.Padding import pad


IV = os.urandom(8)
FLAG = ?


def xor(a, b):
    # xor 2 bytestrings, repeating the 2nd one if necessary
    return bytes(x ^ y for x,y in zip(a, b * (1 + len(a) // len(b))))



@chal.route('/triple_des/encrypt/<key>/<plaintext>/')
def encrypt(key, plaintext):
    try:
        key = bytes.fromhex(key)
        plaintext = bytes.fromhex(plaintext)
        plaintext = xor(plaintext, IV)

        cipher = DES3.new(key, DES3.MODE_ECB)
        ciphertext = cipher.encrypt(plaintext)
        ciphertext = xor(ciphertext, IV)

        return {"ciphertext": ciphertext.hex()}

    except ValueError as e:
        return {"error": str(e)}


@chal.route('/triple_des/encrypt_flag/<key>/')
def encrypt_flag(key):
    return encrypt(key, pad(FLAG.encode(), 8).hex())

Solution

• Trước tiên ta cần hiểu sơ đồ của 3DES:
  
  
• Dựa theo sơ đồ trên, hàm encrypt của DES3 sẽ lấy vào key 32-byte với key1 = key[:8], key2 = key[8:16], key3 = [16:24] (key2 != key1 != key3 nếu không sẽ trở thành DES). Nếu key chỉ có 24-byte thì key1 = key3.
• Thêm một kiến thức nữa ta cần áp dụng trong bài này về khóa yếu. Khóa yếu là các khóa thỏa mãn E(E(weak_key, plaintext)) = plaintext. Kết hợp với sơ đồ 3DES mã hóa ct = E(D(E(key, pt))), nếu thay key = weak_key, pt = FLAG, ta có thể khôi phục lại flag.
• Code:

import requests
from pwn import *
from json import loads
from Crypto.Util.Padding import unpad

def encrypt(key, pt):
    key, pt = bytes.hex(key), bytes.hex(pt)
    url = f"https://aes.cryptohack.org/triple_des/encrypt/{key}/{pt}/"
    r = requests.get(url)
    ct = (loads(r.text))['ciphertext']
    return bytes.fromhex(ct)

def encrypt_flag(key):
    key = bytes.hex(key)
    url = f"https://aes.cryptohack.org/triple_des/encrypt_flag/{key}/"
    r = requests.get(url)
    key = (loads(r.text))['ciphertext']
    return bytes.fromhex(key)

keys = [
    b'\x00'*8 + b'\xff'*8,
    b'\xff'*8 + b'\x00'*8,
    b'\x00\x01\x00\x01\x00\x01\x00\x01\x00\x01\x00\x01\x00\x01\x00\x01',
    b'\x01\x00\x01\x00\x01\x00\x01\x00\x01\x00\x01\x00\x01\x00\x01\x00'
]
for key in keys:
    try:
        enc = encrypt_flag(key)
        flag = unpad(encrypt(key, enc), 8).decode()
        print(flag)
        break
    except:
        print(f'{key}: Error!!!')

Flag

crypto{n0t_4ll_k3ys_4r3_g00d_k3ys}

Note

• Còn một số weak key nữa nhưng ra flag ngay từ key đầu tiên nên mình break luôn.
• Ý tưởng của bài đơn giản nhưng nếu không biết về weak key cũng hơi khó để làm.
• Ban đầu mình định làm theo kiểu brute force từng kí tự như bài ECB Oracle ở trên nhưng bị bí do chưa biết iv , đọc được về weak key nên lụm flag thôi

---

IV. STREAM CIPHERS

15. Symmetry

Description (Translated)

• Một vài chế độ mã hóa khối như OFB, CTR hay CFB có thể chuyển mã khối thành mã dòng. Ý tưởng của mật mã dòng là sinh một dòng khóa ngẫu nhiên rồi XOR với bản rõ. Lợi ích của việc sử dụng mật mã dòng là bản rõ không bị quy chuẩn về độ dài như mật mã khối cần padding.
• OFB là một mode ít được sử dụng ngày nay do yếu hơn mode CTR. Challenge dưới đây khai thác điểm yếu của OFB.
• Play here
• Challenge code:

from Crypto.Cipher import AES


KEY = ?
FLAG = ?


@chal.route('/symmetry/encrypt/<plaintext>/<iv>/')
def encrypt(plaintext, iv):
    plaintext = bytes.fromhex(plaintext)
    iv = bytes.fromhex(iv)
    if len(iv) != 16:
        return {"error": "IV length must be 16"}

    cipher = AES.new(KEY, AES.MODE_OFB, iv)
    encrypted = cipher.encrypt(plaintext)
    ciphertext = encrypted.hex()

    return {"ciphertext": ciphertext}


@chal.route('/symmetry/encrypt_flag/')
def encrypt_flag():
    iv = os.urandom(16)

    cipher = AES.new(KEY, AES.MODE_OFB, iv)
    encrypted = cipher.encrypt(FLAG.encode())
    ciphertext = iv.hex() + encrypted.hex()

    return {"ciphertext": ciphertext}

Solution

• Trước tiên, ta cần phải hiểu sơ đồ mã hóa và giải mã của mode OFB:
  
  
• Có thể thấy, quá trình mã hóa sẽ trở thành giải mã nếu ta thay đổi vị trí của Pi và Ci. Chính vì vậy, bài toán đơn giản trở thành nhận và gửi dữ liệu lại cho web.
• Code:

import requests
from json import loads

def encrypt(plaintext, iv):
    plaintext, iv = bytes.hex(plaintext), bytes.hex(iv)
    url = f'https://aes.cryptohack.org/symmetry/encrypt/{plaintext}/{iv}/'
    r = requests.get(url)
    ct = (loads(r.text))['ciphertext']
    return ct

def encrypt_flag():
    url = f'https://aes.cryptohack.org/symmetry/encrypt_flag'
    r = requests.get(url)
    enc = (loads(r.text))['ciphertext']
    enc = bytes.fromhex(enc)
    iv, ct = enc[:16], enc[16:]
    return iv, ct

iv, ct = encrypt_flag()
flag = bytes.fromhex(encrypt(ct, iv)).decode()
print(flag)

Flag

crypto{0fb_15_5ymm37r1c4l_!!!11!}

Note

• Phân tích flag một chút, 'OFB is symmetrical'. Theo Cambridge, 'symmetrical' có nghĩa: 'một thứ được gọi là symmetrical khi có hai phần giống hệt nhau, hoặc phần này là phản chiếu của phần kia trong gương, hoặc phần này chính là phần kia xoay đi 90° hoặc 180°'. Hay đơn giản hơn, 'symmetrical' có nghĩa là 'đối xứng'. Điều này hoàn toàn đúng với mode OFB theo sơ đồ ở trên. Một vài mode cũng có cơ chế gần tương tự là CFB hoặc CTR.

---

16. Bean Counter

Description

• I've struggled to get PyCrypto's counter mode doing what I want, so I've turned ECB mode into CTR myself. My counter can go both upwards and downwards to throw off cryptanalysts! There's no chance they'll be able to read my picture.
• Play here
• Challenge code:

from Crypto.Cipher import AES


KEY = ?


class StepUpCounter(object):
    def __init__(self, step_up=False):
        self.value = os.urandom(16).hex()
        self.step = 1
        self.stup = step_up

    def increment(self):
        if self.stup:
            self.newIV = hex(int(self.value, 16) + self.step)
        else:
            self.newIV = hex(int(self.value, 16) - self.stup)
        self.value = self.newIV[2:len(self.newIV)]
        return bytes.fromhex(self.value.zfill(32))

    def __repr__(self):
        self.increment()
        return self.value



@chal.route('/bean_counter/encrypt/')
def encrypt():
    cipher = AES.new(KEY, AES.MODE_ECB)
    ctr = StepUpCounter()

    out = []
    with open("challenge_files/bean_flag.png", 'rb') as f:
        block = f.read(16)
        while block:
            keystream = cipher.encrypt(ctr.increment())
            xored = [a^b for a, b in zip(block, keystream)]
            out.append(bytes(xored).hex())
            block = f.read(16)

    return {"encrypted": ''.join(out)}

Solution

• Trước tiên ta cần phân tích source code của bài, có thể thấy step_up=False(=0) dẫn tới self.newIV = hex(int(self.value, 16) hay iv không thay đổi trong quá trình mã hóa, khiến keystream trở thành một chuỗi 16 bytes được lặp lại nhiều lần rồi xor với bản rõ.
• Ta có thể tìm được 16 bytes này. Trước hết ta có keysream(16) ^ flag(??) = ct(??) nên keystream(16) ^ flag(16) = ct(16)
• Ta quan tâm đến 16 bytes đầu của flag vì 16 bytes đầu của file PNG luôn là b'\x89PNG\r\n\x1a\n\x00\x00\x00\rIHDR'. Ta lại biết được 16 bytes đầu của ct, khi đó ta tìm được keystream. Done
• Code:

from requests import get
from PIL import Image
from json import loads
from pwn import xor

def encrypt():
    url = 'https://aes.cryptohack.org/bean_counter/encrypt'
    r = get(url)
    enc = loads(r.text)['encrypted']
    return bytes.fromhex(enc)

first = b'\x89PNG\r\n\x1a\n\x00\x00\x00\rIHDR'
ct = encrypt()

keystream = xor(first, ct[:16])
assert len(keystream) == 16
png_flag = xor(keystream, ct)

image = open('flag.png', 'wb').write(png_flag)
flag = Image.open('flag.png')
flag.show()

Flag

crypto{hex_bytes_beans}

---

17. CTRIME

Description:

• There may be a lot of redundancy in our plaintext, so why not compress it first?
• Play here
• Challenge code:

from Crypto.Cipher import AES
from Crypto.Util import Counter
import zlib


KEY = ?
FLAG = ?


@chal.route('/ctrime/encrypt/<plaintext>/')
def encrypt(plaintext):
    plaintext = bytes.fromhex(plaintext)

    iv = int.from_bytes(os.urandom(16), 'big')
    cipher = AES.new(KEY, AES.MODE_CTR, counter=Counter.new(128, initial_value=iv))
    encrypted = cipher.encrypt(zlib.compress(plaintext + FLAG.encode()))

    return {"ciphertext": encrypted.hex()}

Solution

• Đọc source code xong mình cũng không biết phải làm gì . Phân tích code một chút, đầu tiên hàm encrypt sẽ lấy plaintext mà mình gửi vào dưới dạng hex. Sau khi khởi tạo một iv 16 bytes bất kì và chuyển thành int thì bắt đầu mã hóa với key ẩn, counter 128 bits (16 bytes) và initial_value = iv. Đối tượng mã hóa ở đây là zlib.compress(plaintext + FLAG.encode()) và ta sẽ nhận được ciphertext.
• Bước setup mã hóa khá bảo mật nên mình thử tìm kiếm về cách hoạt động của zlib.compress nhưng không có kết quả.
• Mình đã thử gửi hai pt như sau:

pt1 = bytes.hex(b'crypto') #63727970746f
pt2 = bytes.hex(b'crypto{) #63727970746f7b

• Và thử thay đổi 7b ở pt2 thành các kí tự khác, kết quả là độ dài ciphertext nhận được đã bị thay đổi, cụ thể hơn:
  
  
  
  
• Từ đây mình rút ra là, nếu kí tự mình nhập vào là đúng, len(ct) sẽ cố định. Thử với một vài trường hợp khác, mình nhận ra có một vài kí tự khi gửi lên sẽ làm cho len(ct) bị thay đổi, vậy nên gửi pt lặp lại sẽ chắc chắn hơn, ví dụ thay vì gửi crypto{ thì mình sẽ gửi crypto{crypto{ và check xem nếu trường hợp ct trả về khi mình điền kí tự tiếp theo vào pt có độ dài nhỏ hơn một mức nào đó thì nhận làm kí tự hợp lệ.
• Vậy thì code bài này sẽ là brute force, khá giống với bài ECB Oracle ở trên (thậm chí còn đơn giản hơn):

from json import loads
import requests

def encrypt(pt):
    pt = bytes.hex(pt)
    url = f'https://aes.cryptohack.org/ctrime/encrypt/{pt}/'
    r = requests.get(url)
    ct = (loads(r.text))['ciphertext']
    return ct

FLAG = b'crypto{'
chars = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789_abcdefghijklmnopqrstuvwxyz}'

while True:
    temp = (FLAG + b'.') * 2
    check = len(encrypt(temp))
    for char in chars:
        pt = (FLAG + char.encode()) * 2
        print(char)
        if len(encrypt(pt)) < check:
            FLAG += char.encode()
            print('-'*20)
            print(f'FOUND: {FLAG.decode()}')
            print('-'*20)
            if FLAG.endswith(b'}'): 
                exit()
            break

Flag

crypto{CRIME_571ll_p4y5}

---

18. Logon Zero

Description

• Before using the network, you must authenticate to Active Directory using our timeworn CFB-8 logon protocol.
• Connect at socket.cryptohack.org 13399
• Challenge file:

#!/usr/bin/env python3

from Crypto.Cipher import AES
from Crypto.Util.number import bytes_to_long
from os import urandom
from utils import listener

FLAG = "crypto{???????????????????????????????}"


class CFB8:
    def __init__(self, key):
        self.key = key

    def encrypt(self, plaintext):
        IV = urandom(16)
        cipher = AES.new(self.key, AES.MODE_ECB)
        ct = b''
        state = IV
        for i in range(len(plaintext)):
            b = cipher.encrypt(state)[0]
            c = b ^ plaintext[i]
            ct += bytes([c])
            state = state[1:] + bytes([c])
        return IV + ct

    def decrypt(self, ciphertext):
        IV = ciphertext[:16]
        ct = ciphertext[16:]
        cipher = AES.new(self.key, AES.MODE_ECB)
        pt = b''
        state = IV
        for i in range(len(ct)):
            b = cipher.encrypt(state)[0]
            c = b ^ ct[i]
            pt += bytes([c])
            state = state[1:] + bytes([ct[i]])
        return pt


class Challenge():
    def __init__(self):
        self.before_input = "Please authenticate to this Domain Controller to proceed\n"
        self.password = urandom(20)
        self.password_length = len(self.password)
        self.cipher = CFB8(urandom(16))

    def challenge(self, your_input):
        if your_input['option'] == 'authenticate':
            if 'password' not in your_input:
                return {'msg': 'No password provided.'}
            your_password = your_input['password']
            if your_password.encode() == self.password:
                self.exit = True
                return {'msg': 'Welcome admin, flag: ' + FLAG}
            else:
                return {'msg': 'Wrong password.'}

        if your_input['option'] == 'reset_connection':
            self.cipher = CFB8(urandom(16))
            return {'msg': 'Connection has been reset.'}

        if your_input['option'] == 'reset_password':
            if 'token' not in your_input:
                return {'msg': 'No token provided.'}
            token_ct = bytes.fromhex(your_input['token'])
            if len(token_ct) < 28:
                return {'msg': 'New password should be at least 8-characters long.'}

            token = self.cipher.decrypt(token_ct)
            new_password = token[:-4]
            self.password_length = bytes_to_long(token[-4:])
            self.password = new_password[:self.password_length]
            return {'msg': 'Password has been correctly reset.'}


listener.start_server(port=13399)

Solution

• Sau khi đọc source code, mình đã thử osint về mode CFB8 và cách tấn công thì nhận được về một tài liệu nói về Zerologon Attack như sau
• Về cơ bản, quy trình mã hóa của CFB8 như sau:
  
  
• Mình sẽ phân tích một chút, server cung cấp cho ta ba chức năng là authenticate, reset_connection và reset_password. Trong đó, chức năng authenticate để xác minh admin, chức năng thứ 2 để thay đổi key và chức năng cuối cùng để thay đổi password bằng token mà mình gửi vào (đây chính là nơi mình có thể khai thác điểm yếu). Token nhận vào được decrypt bằng CFB8 tạo thành password mới. Tuy nhiên mode này có điểm yếu đã được giới thiệu ở link trên, cụ thể có thể dùng code dưới đây để check lại:

from Crypto.Util.number import bytes_to_long
from os import urandom
from Crypto.Cipher import AES

key = urandom(16)
def encrypt(plaintext):
    IV = urandom(16)
    cipher = AES.new(key, AES.MODE_ECB)
    ct = b''
    state = IV
    for i in range(len(plaintext)):
        b = cipher.encrypt(state)[0]
        c = b ^ plaintext[i]
        ct += bytes([c])
        state = state[1:] + bytes([c])
    return IV + ct

def decrypt(ciphertext):
    IV = ciphertext[:16]
    ct = ciphertext[16:]
    cipher = AES.new(key, AES.MODE_ECB)
    pt = b''
    state = IV
    for i in range(len(ct)):
        b = cipher.encrypt(state)[0]
        c = b ^ ct[i]
        pt += bytes([c])
        state = state[1:] + bytes([ct[i]])
    return pt

token = b'\x00' * 28
token = decrypt(token)
new_password = token[:-4]
LEN = bytes_to_long(token[-4:])
print(len(new_password[:LEN]))

• Nếu ta gửi token là một chuỗi lặp lại gồm 28 kí tự, password cũng sẽ là một chuỗi lặp lại gồm 8 kí tự. Đến đây idea rõ ràng sẽ là brute force 8 kí tự này cho đến khi nào server nhả flag thì thôi. Ở đây mình chọn token = b'\x00' * 28 (nhưng cũng có thể chọn chuỗi khác) và password để check sẽ là '' cho đỡ phải lặp lại . Brute force thôi:

from pwn import *
from json import *

HOST = 'socket.cryptohack.org'
PORT = 13399

def send(msg):
    return r.sendline(dumps(msg))

r = remote(HOST, PORT)
r.recv()
exploit = b'\x00' * 28

while True:
    option1 = {'option': 'reset_password', 'token': bytes.hex(exploit)}
    send(option1)
    print(r.recv())

    auth = ''
    option2 = {'option': 'authenticate', 'password': auth}
    send(option2)
    get = loads(r.recv())['msg']
    if 'Welcome admin, flag: ' in get:
        print(get)
        break

    option3 = {'option': 'reset_connection'}
    send(option3)
    print(r.recv())

Flag

crypto{Zerologon_Windows_CVE-2020-1472}

Note

• Đây là một bài khá hay, ngay từ khi thấy đoạn check token hơi phức tạp mình đã nảy ra idea cho hết token bằng b'\x00' ai dè trùng luôn cách tấn công CFB8 .

---

19. Stream of Consciousness

Description

• Talk to me and hear a sentence from my encrypted stream of consciousness.
• Play here
• Challenge code:

from Crypto.Cipher import AES
from Crypto.Util import Counter
import random


KEY = ?
TEXT = ['???', '???', ..., FLAG]


@chal.route('/stream_consciousness/encrypt/')
def encrypt():
    random_line = random.choice(TEXT)

    cipher = AES.new(KEY, AES.MODE_CTR, counter=Counter.new(128))
    encrypted = cipher.encrypt(random_line.encode())

    return {"ciphertext": encrypted.hex()}

Solution

• Trên server chỉ cung cấp cho mình duy nhất một chức năng là lấy ct, tuy nhiên điều đặc biệt lưu ý ở đây là key và counter được reused.
• Khi đó, mình nảy ra ý tưởng lấy tất cả các ct về để phân tích vì key và counter không quá quan trọng nữa. Mặc dù mình chưa biết có bao nhiêu ct, nhưng nếu lấy 1000 lần ct thì có thể dự đoán được số lượng (ở đây là 22), code như sau:

from requests import *
from json import *

def encrypt():
    url = f'https://aes.cryptohack.org/stream_consciousness/encrypt/'
    r = get(url)
    return loads(r.text)['ciphertext']

stream = []
for _ in range(1000):
    temp = encrypt()
    if temp not in stream:
        stream.append(temp)
        print(len(stream))

stream = sorted(stream, key=len)
print(stream)

• Tại đây mình đồng thời sort luôn cho tiện. Đại khái những ct nhận được là:

be9065d98ec30981b8b90bfb41
b39063c6e7b41691f4ba5efa16a35056093b7403
b08b73c6e7b41290f9ba12a917ab49191337394488a6
b5977295ddb90c99f3bf10ee5ead4912411f704190e1d71846e3
92976e96dafb1a93abaf4bbe0cff131b3e202a58c9bbe64c01c5fb6061d51c9d
a68d76928ef54196f9a50af05ebf4a130d3e395994e1ca5d44fbf43a22c118818347
b8913785cffa468cb8b41ba90aa35518413d6c59d0a8db0840baf4207682118ec70b7fdc10e71b173974c60a
b8c5648ecff80dd8f4b90dec5ea95113132b6d4595e6de5d55f4f974388e04c0800c6edc11e918582970c14f71
a58d6583cbb40397e1a55efb0ba2491f0f35350d8ce4d8045df4fa7437955088881b69990aac552b2e63db4b256ec957
b096378fc8b428d8f0b71aa91fa25e56163b6a45dcfcd65d56ffbd3d38c10488824968951ee801596b5882473e688f02f8
bf8a3bc6e7b30d94b8b111a917a207020e725d4290e4c05d55f4f97422841c8cc7017f8e59f3010a2a78c54c2b26c703ad
b98a60c6dee60e8dfcf61fe71aec4f171122600d94ed9e1158baff31769618858949729959e7100c3831cf5d7f68c702bcb8
a68d6ec6cafb418cf0b307a919a307190f72694c95e6cd145afdbd35388550829200769810ee12582a7dce042b6ecd56adf065ddbe
b8c5648ecff80dd4b89f59e512ec4b19123739488aedcb0440f2f43a31c11986c7017fdc1def100b2536d6043c69c513f9fb69dbea4e
a58d72c6daf1138af1b412ec5eb84f1f0f3539448fa8cd1555eebd203e845090861a6edc1ae11b5f3f31c0417f72c704b7b967cdf5403ae08481cc770641d19122ab01
a68a628acab428d8f0b708ec5eae421a08376f4898a8cd1551f4bd203e8004c0ae4979930cec11583974c3473726db03baf128dce4102cf1d7c8d762065bcb933fb4463501a4e02b0a   
a180658ecfe412d8f0b35ee11fbf071b08216a4898a8cd1551bae92637881ec086077edc10f3551a2a72c9043d7f8818b6ee2698d60136ed8485d7764313d68b3bb1433d14b9e62a5b1f 
b8c27ac6dbfa0999e8a607a55e85071204217c5f8aed991440b6bd203e845086861c76885ef35515227fc7087f64dd02f9d02fd5a11536f1c598c87d0652d29276ac473155beee2850123af77a47ca7588bd5f
bd8a618382b4118af7b41feb12b51856353a7c54dcecd61313eebd3f388e07c08f066ddc1df210193968824d2b26c105f5b960d7f64030ecc981d46d4747d79031f6017a55b9e720157f6cfa715edf7584b615e96e659520c714359a1a
b58a7b8ad7b41691f4ba5efd16a5491d4126714c88a8f05a59baf1313797198e80497bdc0ae516172575824c2a75ca17b7fd28d9ef0478edcc89cc24525bdb8c33be402610edc665584b69eb3f58cf2780b408e96f68dc25cd46249c51614cccfca866d8
a58d7295cbb40997eaa51bfa52ec531e0821394e9dfacb1455fdf8747bc1188f904953dc15ef140c237482492675cd1abfb961d6a11430f0d7c8db655441d79f31bd0f7955b9e7204c1968fa3f4ad639c5b018ba362d9e39d74619d447295ad2ffe66f932603fe7a2af2f968e471b7c5675759d26ec1ce
a68d76928ef54194f7a25ee618ec531e083c7e5edcfcd11c40bae93c338f5093820c77991da001176b7cc7042c69881bb8eb7edded0c37ecd7c8d96a4213cb9037ac5b351ca3ee27595b36bf774acc30c5ba14aa6260996cca08239d532f52d8faa56098244aac3b37f3bc3cf87cf2dc2f5f50d4748fa92da5730f18b904a1cbf57534ed4393f668ccd755fb360203d80434c04e4b481cddff7780ad9afcf6

• Thực ra thì đọc bài này làm mình nhớ lại một chall ở CTFlearn: ALEXCTF CR2: Many time secrets. Chall này thì mình làm rồi, khá dễ và thuộc dạng guessing ít phải suy nghĩ. Quay lại với bài, biết được mode CTR với key và counter yếu, khi đó mình có:

X ^ P[i] = C[i]
nên P[i] ^ P[i-1] = C[i] ^ C[i-1]

với X = D(key, counter).

• Tới đây mình sẽ tạo ra các tổ hợp chập 2 của 22 phần tử trong stream và xor với nhau, đồng thời xor với flag = b'crypto{' để khai thác vì kiểu gì 1 trong 22 ct cũng là của flag:

from pwn import xor
from itertools import combinations

stream = ['be9065d98ec30981b8b90bfb41', 'b39063c6e7b41691f4ba5efa16a35056093b7403', 'b08b73c6e7b41290f9ba12a917ab49191337394488a6', 'b5977295ddb90c99f3bf10ee5ead4912411f704190e1d71846e3', '92976e96dafb1a93abaf4bbe0cff131b3e202a58c9bbe64c01c5fb6061d51c9d', 'a68d76928ef54196f9a50af05ebf4a130d3e395994e1ca5d44fbf43a22c118818347', 'b8913785cffa468cb8b41ba90aa35518413d6c59d0a8db0840baf4207682118ec70b7fdc10e71b173974c60a', 'b8c5648ecff80dd8f4b90dec5ea95113132b6d4595e6de5d55f4f974388e04c0800c6edc11e918582970c14f71', 'a58d6583cbb40397e1a55efb0ba2491f0f35350d8ce4d8045df4fa7437955088881b69990aac552b2e63db4b256ec957', 'b096378fc8b428d8f0b71aa91fa25e56163b6a45dcfcd65d56ffbd3d38c10488824968951ee801596b5882473e688f02f8', 'bf8a3bc6e7b30d94b8b111a917a207020e725d4290e4c05d55f4f97422841c8cc7017f8e59f3010a2a78c54c2b26c703ad', 'b98a60c6dee60e8dfcf61fe71aec4f171122600d94ed9e1158baff31769618858949729959e7100c3831cf5d7f68c702bcb8', 'a68d6ec6cafb418cf0b307a919a307190f72694c95e6cd145afdbd35388550829200769810ee12582a7dce042b6ecd56adf065ddbe', 'b8c5648ecff80dd4b89f59e512ec4b19123739488aedcb0440f2f43a31c11986c7017fdc1def100b2536d6043c69c513f9fb69dbea4e', 'a58d72c6daf1138af1b412ec5eb84f1f0f3539448fa8cd1555eebd203e845090861a6edc1ae11b5f3f31c0417f72c704b7b967cdf5403ae08481cc770641d19122ab01', 'a68a628acab428d8f0b708ec5eae421a08376f4898a8cd1551f4bd203e8004c0ae4979930cec11583974c3473726db03baf128dce4102cf1d7c8d762065bcb933fb4463501a4e02b0a', 'a180658ecfe412d8f0b35ee11fbf071b08216a4898a8cd1551bae92637881ec086077edc10f3551a2a72c9043d7f8818b6ee2698d60136ed8485d7764313d68b3bb1433d14b9e62a5b1f', 'b8c27ac6dbfa0999e8a607a55e85071204217c5f8aed991440b6bd203e845086861c76885ef35515227fc7087f64dd02f9d02fd5a11536f1c598c87d0652d29276ac473155beee2850123af77a47ca7588bd5f', 'bd8a618382b4118af7b41feb12b51856353a7c54dcecd61313eebd3f388e07c08f066ddc1df210193968824d2b26c105f5b960d7f64030ecc981d46d4747d79031f6017a55b9e720157f6cfa715edf7584b615e96e659520c714359a1a', 'b58a7b8ad7b41691f4ba5efd16a5491d4126714c88a8f05a59baf1313797198e80497bdc0ae516172575824c2a75ca17b7fd28d9ef0478edcc89cc24525bdb8c33be402610edc665584b69eb3f58cf2780b408e96f68dc25cd46249c51614cccfca866d8', 'a58d7295cbb40997eaa51bfa52ec531e0821394e9dfacb1455fdf8747bc1188f904953dc15ef140c237482492675cd1abfb961d6a11430f0d7c8db655441d79f31bd0f7955b9e7204c1968fa3f4ad639c5b018ba362d9e39d74619d447295ad2ffe66f932603fe7a2af2f968e471b7c5675759d26ec1ce', 'a68d76928ef54194f7a25ee618ec531e083c7e5edcfcd11c40bae93c338f5093820c77991da001176b7cc7042c69881bb8eb7edded0c37ecd7c8d96a4213cb9037ac5b351ca3ee27595b36bf774acc30c5ba14aa6260996cca08239d532f52d8faa56098244aac3b37f3bc3cf87cf2dc2f5f50d4748fa92da5730f18b904a1cbf57534ed4393f668ccd755fb360203d80434c04e4b481cddff7780ad9afcf6']

flag = b'crypto{'
stream = list(combinations(stream, 2))

for comb in stream:
    temp = xor(bytes.fromhex(comb[0]), bytes.fromhex(comb[1]))[:len(flag)]
    res = xor(temp, flag)
    print(res)

nhận được một vài pt khá rõ ràng:

b'What a '
b"It can'"
b'I shall'
b'Three b'
b'As if I'
b"No, I'l"
b'How pro'
b'Why do '
b'I shall'
b'The ter'
b'Would I'
b'Perhaps'
b"I'm unh"
b'Love, p'
b'Dolly w'
b'These h'

• Về phần việc tiếp theo, mình cần áp dụng crib dragging để guess và thu lại các text vụn trong bài, quy trình mình thử như sau:

flag = b'crypto{'
flag = b"I'm unhappy"
flag = b'Love, probably'
flag = b'And I shall ignore'
flag = b'Would I have believed'
flag = b'I shall lose everything'
flag = b"I shall, I'll lose everything"
flag = b"Dolly will think that I'm leaving"

• Tới đây thì nhận được flag rồi, done

Flag

crypto{k3y57r34m_r3u53_15_f474l}

Note

• Mình cũng định ngồi thử guess xem thông điệp ở đây là gì nhưng thực sự nó khá khó, vì ct được scrambled dẫn đến pt cũng không còn nguyên vẹn, nếu có cũng chỉ là các fragment mà thôi.
• Tuy nhiên ở lời giải cũng có bác Masrt thử recover lại, khá ngầu

---

20. Dancing Queen

Description

• I don't trust other developers so I made my own ChaCha20 implementation. In this way, I am sure you will never be able to read my flag!
• Challenge code:

#!/usr/bin/env python3

from os import urandom


FLAG = b'crypto{?????????????????????????????}'


def bytes_to_words(b):
    return [int.from_bytes(b[i:i+4], 'little') for i in range(0, len(b), 4)]

def rotate(x, n):
    return ((x << n) & 0xffffffff) | ((x >> (32 - n)) & 0xffffffff)

def word(x):
    return x % (2 ** 32)

def words_to_bytes(w):
    return b''.join([i.to_bytes(4, 'little') for i in w])

def xor(a, b):
    return b''.join([bytes([x ^ y]) for x, y in zip(a, b)])


class ChaCha20:
    def __init__(self):
        self._state = []

    def _inner_block(self, state):
        self._quarter_round(state, 0, 4, 8, 12)
        self._quarter_round(state, 1, 5, 9, 13)
        self._quarter_round(state, 2, 6, 10, 14)
        self._quarter_round(state, 3, 7, 11, 15)
        self._quarter_round(state, 0, 5, 10, 15)
        self._quarter_round(state, 1, 6, 11, 12)
        self._quarter_round(state, 2, 7, 8, 13)
        self._quarter_round(state, 3, 4, 9, 14)

    def _quarter_round(self, x, a, b, c, d):
        x[a] = word(x[a] + x[b]); x[d] ^= x[a]; x[d] = rotate(x[d], 16)
        x[c] = word(x[c] + x[d]); x[b] ^= x[c]; x[b] = rotate(x[b], 12)
        x[a] = word(x[a] + x[b]); x[d] ^= x[a]; x[d] = rotate(x[d], 8)
        x[c] = word(x[c] + x[d]); x[b] ^= x[c]; x[b] = rotate(x[b], 7)
    
    def _setup_state(self, key, iv):
        self._state = [0x61707865, 0x3320646e, 0x79622d32, 0x6b206574]
        self._state.extend(bytes_to_words(key))
        self._state.append(self._counter)
        self._state.extend(bytes_to_words(iv))

    def decrypt(self, c, key, iv):
        return self.encrypt(c, key, iv)

    def encrypt(self, m, key, iv):
        c = b''
        self._counter = 1

        for i in range(0, len(m), 64):
            self._setup_state(key, iv)
            for j in range(10):
                self._inner_block(self._state)
            c += xor(m[i:i+64], words_to_bytes(self._state))

            self._counter += 1
        
        return c
    

if __name__ == '__main__':
    msg = b'Lorem ipsum dolor sit amet, consectetuer adipiscing elit. Aenean commodo ligula.'
    key = urandom(32)
    iv1 = urandom(12)
    iv2 = urandom(12)

    c = ChaCha20()
    msg_enc = c.encrypt(msg, key, iv1)
    flag_enc = c.encrypt(FLAG, key, iv2)

    print(f"iv1 = '{iv1.hex()}'")
    print(f"iv2 = '{iv2.hex()}'")
    print(f"msg_enc = '{msg_enc.hex()}'")
    print(f"flag_enc = '{flag_enc.hex()}'")

• Challenge ouput:

iv1 = 'e42758d6d218013ea63e3c49'
iv2 = 'a99f9a7d097daabd2aa2a235'
msg_enc = 'f3afbada8237af6e94c7d2065ee0e221a1748b8c7b11105a8cc8a1c74253611c94fe7ea6fa8a9133505772ef619f04b05d2e2b0732cc483df72ccebb09a92c211ef5a52628094f09a30fc692cb25647f'
flag_enc = 'b6327e9a2253034096344ad5694a2040b114753e24ea9c1af17c10263281fb0fe622b32732'

Solution

• Trước hết mình sẽ phân tích source code của bài kết hợp với osint. ChaCha20 là một loại mã dòng gồm 20 vòng, nhanh hơn AES. Vì là mã dòng nên len(flag) = len(flag_enc) = 74. No more idea