# 【LeetCode】 1971. Find if Path Exists in Graph

## Description
> There is a bi-directional graph with `n` vertices, where each vertex is labeled from `0` to `n - 1` (inclusive). The edges in the graph are represented as a 2D integer array `edges`, where each `edges[i] = [ui, vi]` denotes a bi-directional edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
> You want to determine if there is a valid path that exists from vertex `source` to vertex `destination`.
> Given edges and the integers `n`, `source`, and `destination`, return `true` if there is a valid path from `source` to `destination`, or `false` otherwise.

> 有一個包含 `n` 個頂點的雙向圖，每個點被標記成 `0` 到 `n - 1` (包含)。圖中的邊使用二維整數陣列 `deges` 表示，`edges[i] = [ui, vi]` 表示一條在頂點 `ui` 和 `vi` 的雙向邊。每個頂點對之間只會有一條邊，且不會有點自己連結到自己。
> 你需要判斷從頂點 `source` 到 `destnation` 之間是否存在一條合法路徑。
> 給予 `edges` 和整數 `n`、`source` 和 `destination`，回傳 `true` 如果 `source` 到 `destination` 之間有一條合法路徑，否則回傳 `false`。

## Example:


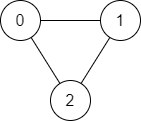
Example 1:

Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
- 0 → 2


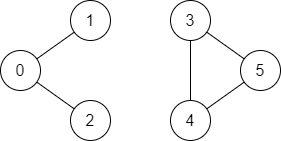
Example 2:

Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.

## Solution

* 標準的 DFS/BFS 題目
* 先建立好圖中每個節點的關係，然後每個點遍歷一次即可
* 為了節省時間，節點中加入了 `touched` 屬性，代表該點是否已經走過
* 走過的路就不要再走
* 下面範例中，BFS 演算法多宣告了 `vector<node> stack` 去記錄目前的待走節點
* 如果改用遞迴的方式實作 DFS，直接在 function stack 中完成紀錄，可以節省一些空間資源

### Code

class Solution {
public:
    struct node
    {
        int name;
        vector<int> next;
        bool touched;
    };

    bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
        if(source == destination)
            return true;
        vector<node> nodes;
        for(int i = 0; i < n; i++)
        {
            node temp;
            temp.name = i;
            temp.touched = false;
            nodes.push_back(temp);
        }
        for(int i = 0; i < edges.size(); i++)
        {
            int a = edges[i][0];
            int b = edges[i][1];
            nodes[a].next.push_back(b);
            nodes[b].next.push_back(a);
        }
        //BFS
        vector<node> stack;
        stack.push_back(nodes[source]);
        while(!stack.empty())
        {
            for(int i = 0; i < stack.front().next.size(); i++)
            {
                if(stack.front().next[i] == destination)
                    return true;
                else if(nodes[stack.front().next[i]].touched == false)
                {
                    nodes[stack.front().next[i]].touched = true;
                    stack.push_back(nodes[stack.front().next[i]]);
                }
            }
            stack.erase(stack.begin());
        }
        return false;
    }
};

###### tags: `LeetCode` `C++`