# 高一用淺薄偏微分
作者:TudoHuang

Tudohuang的奇妙課業
從一年前，為了了解AI，我去學習了偏微分這個概念。
我對了偏微分的了解就是"多元微分"。
恩，沒了
高一數學科的單元如下:
- 數式
- 圓與直線
- 高次方程
- 數列
- 排列組合
- 機率
- 數學期望值
- 一維數據分析
以上都跟微積分的關係(至少就高中來看)沒什麼關係。最有關係的可能是高次方程式，但那也不用用到多元，所以偏微分一直沒什麼實際的應用。
直到.....

## 二維數據分析
我在這一個章節，找到了高一中能夠玩偏微分的機會了!
而這個機會就是: **最小平方法**
### 最小平方法
我們想要找到一條直線
$y = ax+b$
可以最為擬合所有的數據點
EX: $(0,0),(1,1),(2,2),(3,3),(4,4)$
最為擬合這些數據點的直線方程式就是
$y=1x+0$ Easy as a pie
那...如果數據點是
$(1,1),(1,2),(2,2),(2,3)$
你要怎麼做呢?
可以使用最小平方法! SSE(Sum Square Error)!
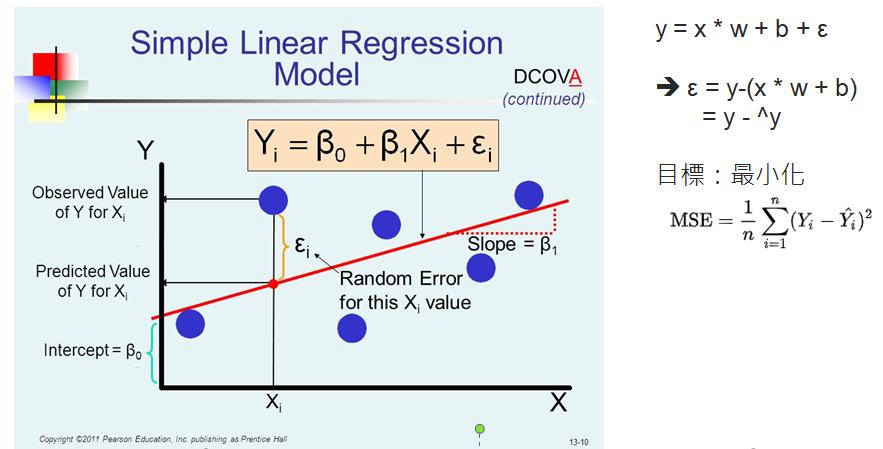
那如何做呢?

#### 課本做法
設直線$f(x) = y=ax+b$
把各個$x$代入，得出:
$y_1=a+b$
$y_2=a+b$
$y_3=2a+b$
$y_4=2a+b$
那$SSE=\sum_{i=1}^4(y_i)^2$
看不懂?
$SSE = (a+b-1)^2+(a+b-2)^2+(2a+b-2)^2+(2a+b-3)^2$
乘開!
$SSE = a^2 + 2ab - 2a + b^2 - 2b + 1 + a^2 + 2ab - 2a + b^2 - 2b + 4 + 4a^2 + 4ab - 8a + b^2 - 4b + 4 + 4a^2 + 4ab - 12a + b^2 - 6b + 9$
x!這是什麼????
把它簡化:
$SSE = 10a^2 + 12ab - 26a + 4b^2 - 16b + 18$
然後經過一些神奇的配方(有點詭異)
$SSE= 10a^2 + 12ab - 26a + 4b^2 - 16b + 18$
$SSE =4b^2 +4(3a-4)b+10a^2-26a+18$
$SSE =[2b+(3a-4)]^2-(3a-4)^2+10a^2-26a+18$
$SSE = (2b+3a-4)^2+a^2-2a+2$
$SSE = (3a+2b-4)^2+(a-1)^2+1$
$$\left\{
\begin{aligned}
3a + 2b -4&= 0 \\
a -1&= 0
\end{aligned}
\right.
$$
得出$a=1,b=\frac{1}{2}$
wow~~ finally! 好累~

#### 偏微分
偏微分就是多元微分。
how to use?
$f(x,y)=x^2+y^2+2xy+2x+2y+1$
如何導數?
BTW，導數是啥?
定義:$f'(a)=\lim_{{h \to 0}} \frac{f(a + h) - f(a)}{h}$
導數代表了一個函數在某一點上的瞬間變化率
恩，我知道看起來很詭異，所以更好算的算法就是
$f(x)= kx^i$
$f'(x)=k\times ix^{i-1}$
EX:
$f(x)=x^2, g(x)=2x$
$f'(x)=2x, g(x)=2$
OK，那多元呢?
回到剛剛那一題，多元微分就是要運用到偏微分$\frac{\partial f}{\partial x}(a, b)$
cool~
來試著看看剛剛那題:
$f(x,y)=x^2+y^2+2xy+2x+2y+1$
要微分它，首先要先拆分成微分x及微分y兩部分
$\frac{\partial f}{\partial x} = 2x+0+2y+2+0+0$(在這裡，y會視作常數)
$\frac{\partial f}{\partial y} = 0+2y+2x+0+2+0$(同理，x會視作常數)

-----
終於回到剛剛那一題最小平方法，直接到簡化後的算式:
$SSE=10a^2 + 12ab - 26a + 4b^2 - 16b + 18$
來吧!召喚偏微分!
$\frac{\partial SSE}{\partial a} = 20a+12b-26+0-0+0$
$\frac{\partial SSE}{\partial b} = 0+12a-0+8b-16+0$

$$\left\{
\begin{aligned}
20a + 12b -26&= 0 \\
12a+8b-16&= 0
\end{aligned}
\right.
$$
整理一波~
$$\left\{
\begin{aligned}
40a + 24b &= 52 \\
36a+24b&= 48
\end{aligned}
\right.
$$

$a=1$
$b=\frac{1}{2}$
秒殺~

-----------------------------

## 高三補筆
看了當年的做法 覺得真是愚鈍
來重寫一次!

從這裡開始
$$E = (a+b-1)^2+(a+b-2)^2+(2a+b-2)^2+(2a+b-3)^2$$

$$\frac{\partial E}{\partial a} = 2(a+b-1)+2(a+b-2)+2(2)(2a+b-2)+2(2)(2a+b-3) = 20a+12b-26 = 0 $$

$$\frac{\partial E}{\partial b} = 2(a+b-1)+2(a+b-2)+2(2a+b-2)+2(2a+b-3) = 12a+8b-16 = 0 $$

||到底誰會真的乘開來啦!||

$$\left\{
\begin{aligned}
40a + 24b &= 52 \\
36a+24b&= 48
\end{aligned}
\right.
$$

$a=1$
$b=\frac{1}{2}$
秒殺~

----------

Bonus:
因為

$$\left\{
\begin{aligned}
\frac{\partial D}{\partial a} =\sum^n_{i=1} (-1)(y_i - a -bx_i) = 0 \\
\frac{\partial D}{\partial b} = \sum^n_{i=1}(-x_i)(y_i - a -bx_i) = 0
\end{aligned}
\right.
$$

$$
\left\{\begin{aligned}
\sum^n_{i=1} y_i = na + b\sum^n_{i=1}x_i \\
\sum^n_{i=1} x_iy_i = a \sum^n_{i=1}x_i+ b\sum^n_{i=1}x_i^2
\end{aligned}
\right.
$$

根據克拉瑪公式能得出通解:
$$
a= \frac{\begin{pmatrix}
\sum y & \sum x \\
\sum xy & \sum x^2
\end{pmatrix}}{\begin{pmatrix}
n & \sum x \\
\sum x & \sum x^2
\end{pmatrix}} = \frac{\sum x^2 \sum y - \sum x\sum xy}{n\sum x^2 - (\sum x)^2}, \quad
b= \frac{\begin{pmatrix}
n & \sum y \\
\sum x & \sum xy
\end{pmatrix}}{\begin{pmatrix}
n & \sum x \\
\sum x & \sum x^2
\end{pmatrix}} = \frac{x\sum xy \sum x\sum y - \sum x\sum xy}{n\sum x^2 - (\sum x)^2}
$$