# Quiz on 2019-05-21
:::warning
重新整理共筆內容,使其符合下方描述框架:
1. 解題思路
2. 由 C 語言規格和實驗 (如 gdb 的操作),分析提出的程式碼
3. 延伸思考二補數系統中的特性
刪去概念上重複的材料並附上參考資料
:::
- [ ] Q1: 用 bitwise operator 實作常數時間複雜度的 abs (取絕對值)。在二補數系統中,輸入有號 32 位元整數,補完以下程式碼:
```cpp=
#include <stdint.h>
int32_t abs(int32_t x) {
int32_t mask = x >> 31;
return ____________;
}
```
第 4 行敘述不得出現 branch 和減法。除了實作程式碼,需要一併解釋運作原理。
:notes:
## 解題思路
* `mask` 是一個提示,先確認 mask 之數值
* `mask` 數值在非負數時是 `0`,負數時是 `-1`
* 觀察 `mask`、輸入值、期望值三者關聯
* bitwise operator
## 實驗
### `mask` 是一個提示,先確認 mask 之數值
以底下程式碼做範例
```cpp=
#include <stdint.h>
#include <limits.h>
#include <stdio.h>
int32_t abs_test(int32_t x){
int32_t mask = x >> 31;
return mask;
}
int main(void){
printf("abs_test(%d) => %d\n", 1, abs_test(1));
printf("abs_test(%d) => %d\n", INT_MAX, abs_test(INT_MAX));
printf("abs_test(%d) => %d\n", 0, abs_test(0));
printf("abs_test(%d) => %d\n", -1, abs_test(-1));
printf("abs_test(%d) => %d\n", INT_MIN, abs_test(INT_MIN));
return 0;
}
```
程式執行結果
```bash=
root:~/ # ./abs_test.out
abs_test(1) => 0
abs_test(2147483647) => 0
abs_test(0) => 0
abs_test(-1) => -1
abs_test(-2147483648) => -1
```
### `mask` 數值在非負數時是 `0`,負數時是 `-1`
* 現代作業系統皆使用 [Two's complement](https://en.wikipedia.org/wiki/Two%27s_complement)
* 負數的 MSB 為 `1`,非負數的 MSB 則為 `0`
* `abs` function 在一開始將輸入的數值 right shift 31 bit
* Shift operator 在使用時有兩種 shift 的方式
* Arithmetic shift
* 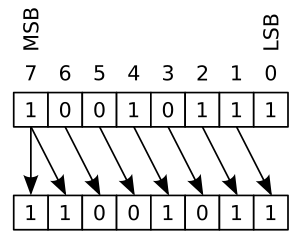
* Right shift 時,空出的 bit 填 MSB
* Left shift 時,空出的 bit 填 0
* Logical shift
* 
* Right 與 Left shift 時,空出的 bit 皆填 0
* 怎麽知道編譯器使用哪種 shift 方式 ?
* [C99 Standard - 6.5.7.5](http://www.open-std.org/jtc1/sc22/wg14/www/docs/n1124.pdf)
* The result of `E1 >> E2` is `E1` right-shifted `E2` bit positions. If `E1` has an unsigned type or if `E1` has a signed type and a nonnegative value, the value of the result is the integral part of the quotient of `E1` / 2^`E2`. **If `E1` has a signed type and a negative value, the resulting value is implementation-defined.**
* [Re: right shift of signed type - GCC](https://gcc.gnu.org/ml/gcc/2000-04/msg00152.html)
* `An arithmetic left shift is equivalent to a logical left shift`
* `For right shifts, if the type is signed, then we use an arithmetic shift;if the type is unsigned then we use a logical.`
* 題目使用的 Data type 為 `signed 32bit integer`,故 right-shift 時採用 Arithmetic shift
* 在輸入負數時,`mask` 之數值為 32 個 1,即為 `-1`,輸入非負數時,`mask` 之數值則為 32 個 0,即為 `0`
### 觀察 `mask`、輸入值、期望值三者關聯
* `3`
```
00000000000000000000000000000011 (Input: 3)
00000000000000000000000000000000 (Mask: 0)
00000000000000000000000000000011 (Goal: 3)
```
* `-2019`
```
11111111111111111111100000011101 (Input: -2019)
11111111111111111111111111111111 (Mask: -1)
00000000000000000000011111100011 (Goal: 2019)
```
* 若把 `-2019` 減一
```
11111111111111111111100000011100 (-2020)
00000000000000000000011111100011 (2019)
```
可以發現只要把 `-2020` 做 bit-flip,就是我們要找的數值
而 `-2020` 這數值在 Ones' complement 中正是 `-2019`
## bitwise operator
* `Bitwise AND (&)`
| bit a | bit b | bitwise `&` |
| ------ | ------ | ----------- |
|0 |0 |0 |
|1 |0 |0 |
|0 |1 |0 |
|1 |1 |1 |
* `Bitwise OR (|)`
| bit a | bit b | bitwise `|` |
| ------ | ------ | ----------- |
|0 |0 |0 |
|1 |0 |1 |
|0 |1 |1 |
|1 |1 |1 |
* `Bitwise XOR(^)`
| bit a | bit b | bitwise `^` |
| ------ | ------ | ----------- |
|0 |0 |0 |
|1 |0 |1 |
|0 |1 |1 |
|1 |1 |0 |
:::info
**透過對 `-1` 做 XOR 可以達到 bit flip 的效果**
:::
我們想要讓負數**減一後 bit flip**
而減一等同於**加上負一**,再加上上面的提示
而因為負數時 **mask 數值為負一**,所以我們可以利用 mask 來達成絕對值
:::info
mask 只會有兩種數值,`0` 或 `-1`
任何數對 `0` 做加減、OR、XOR 皆不影響該數
所以若只使用到上述四種運算方式,我們可以不用顧慮非負數的情形
:::
我們從上面觀察到對負數加負一再進行 bit flip 可以達到取絕對值
即為
```
(gdb) p/t -3 + (-3 >> 31)
$6 = 11111111111111111111111111111100
```
```
11111111111111111111111111111101
+ 11111111111111111111111111111111
------------------------------------
(1)11111111111111111111111111111100
```
:::warning
此處會發生 Overflow,可是 Overflow 後之數值正好是我們要找的數值做 bit-flip 後之數值
以上述數值為例
```
(1)11111111111111111111111111111100
00000000000000000000000000000011
```
:::
```
(gdb) p/t (-3 + (-3 >> 31)) ^ (-3 >> 31)
$7 = 11
```
```
11111111111111111111111111111100
^ 11111111111111111111111111111111
------------------------------------
00000000000000000000000000000011
```
驗證同樣的操作在非負數下不影響數值
```
(gdb) p/t 2019 + (2019 >> 31)
$8 = 11111100011
```
```
00000000000000000000011111100011
+ 00000000000000000000000000000000
------------------------------------
00000000000000000000011111100011
```
```
(gdb) p/t (2019 + (2019 >> 31)) ^ (2019 >> 31)
$9 = 11111100011
```
故得
```cpp
int32_t abs(int32_t x){
int32_t mask = x >> 31;
return ((x + mask) ^ mask);
}
```
## 補充/參照
### Two's complement
底下兩個 equation 分別代表著將 w 個 bit 轉為 Two's complement 與 Ones' complement 的數值
$B2T_{w}(\vec{x})=-x_{w-1}2^{w-1} + \sum_{i=0}^{w-2}x_i2^i$
$B2O_{w}(\vec{x})=-x_{w-1}(2^{w-1} - 1) + \sum_{i=0}^{w-2}x_i2^i$
考慮 `10000000000000000000000000000000`
* Two's complement 之數值為 `-1*2^31 = -(2^31)`
* Ones' complement 之數值為 `-1*(2^31 - 1) = -(2^31 - 1)`
若考慮 `11111111111111111111111111111111`
* Two's complement 定義此數為 `-1`
* Ones' complement 定義此數為 `-0`
這反映出了一件事,就是在負數時, Two's complement 的數值與 Ones' complement 的數值剛好差一
而在 Ones' complement 中,所有的數值都有對應的補數,如
* 2 與 -2 -> `0010` 與 `1101`
* 6 與 -6 -> `0110` 與 `1001`
* 0 與 -0 -> `0000` 與 `1111` (bit 全為 1 被定義為 -0)
這意味著**在 Ones' complement 中,只要做 bit-flip 就可以轉換數值的正負**
接下來看一些極值
* `01111111111111111111111111111111` (32bit signed int 正極值)
* Two's complement: 2^31 - 1
* Ones' complement: 2^31 - 1
* `11111111111111111111111111111111` (32bit signed int 負極值)
* Two's complement: -(2^31)
* Ones' complement: -(2^31 - 1)
在只有 signed bit 不同的狀況下, 可以看到 **Two's complement 能比 Ones' complement 多表達一個數值,就是 -(2^31)**
但這是個有趣的數值,因為這個數值**沒辦法在同一個 N bit 中表達他的正數**
我們從 Two's complement 的定義就可以發現這件事
:::info
Sample code
```
#include <stdio.h>
#include <stdint.h>
int32_t abs_test(int32_t x){
int mask = x >> 31;
printf("%d\n", mask);
printf("%d\n", (x+mask));
return (x + mask) ^ mask;
}
int main(void){
printf("%d\n", abs_test(-2147483648));
return 0;
}
```
```
-1
2147483647
-2147483648
```
此外,依據 [Absolute Value (The GNU C Library)](https://www.gnu.org/software/libc/manual/html_node/Absolute-Value.html) 內文
```
Most computers use a two’s complement integer representation, in which the absolute value of INT_MIN (the smallest possible int) cannot be represented; thus, abs (INT_MIN) is not defined.
```
:::
```clike
// INT_MAX 之數值為 (2^31 - 1)
// INT_MIN 定義為 -INT_MAX - 1
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
int main(void){
printf("%d\n", abs(-INT_MAX));
printf("%d\n", abs(INT_MIN));
return 0;
}
```
```
2147483647
-2147483648
```
### 延伸閱讀:
* [Bit Twiddling Hacks](http://graphics.stanford.edu/~seander/bithacks.html#IntegerAbs)
* [解讀計算機編碼](https://hackmd.io/s/rylUqXLsm)
---
- [ ] Q2: 承 Q1,提出驗證上述程式碼的有效方案,並得以擴展到 `int64_t` 甚至更寬位元的整數型態。
:notes:
:::info
[Boolean Satisfiability Problem (SAT problem)](https://en.wikipedia.org/wiki/Boolean_satisfiability_problem)
Definition: The problem of determining if there exists and interpretation that satisfies a given Boolean formula
簡單來說,給你一個布林方程式,問是否可以找到一組變數賦值,使布林方程式之值為真
:::
---
利用**二補數**特性完成無分支版本的 `abs()` (取絕對值)
```cpp
#include <stdint.h>
int64_t abs64(int64_t x) {
int64_t y = x >> (64 - 1);
return (x ^ y) - y;
}
```
解題思路:
+ 這題其實很直觀,因為**二補數**的提示相當明顯
+ 首先用 `y` 來拿到 `x` 的 sign bit
+ 注意,因為 sign extension,所以 `y` 可能為 `0b000...0 (0)` 或 `0b111...1 (-1)`
+ 接著,若 `y` 為 `0` (`x` 正數),則 `(x ^ 0) - 0` 還是 `x` 本身
+ 若 `y` 為 `-1` (`x` 負數),則 `(x ^ -1) - (-1)` 恰好是透過二補數將負轉正
延伸議題: overflow
```cpp
#include <stdio.h>
#include <limits.h>
#include <float.h>
int main(void) {
if (-2147483648 > 0) printf("positive\n");
if (-2147483647 - 1 < 0) printf("negative\n");
if (INT_MIN == -INT_MIN) printf("equal\n");
if (FLT_MIN > 0) printf("floating\n");
return 0;
}
```
編譯警告
```
int_min.c:9:17: warning: integer overflow in expression [-Woverflow]
if (INT_MIN == -INT_MIN) printf("equal\n");
```
執行結果:
```shell
negative
equal
floating
```
+ 參考資料:[Hard to C - INT_MIN](http://hardtoc.com/2009/07/16/int-min.html)
+ 參考資料: [glibc.git/include/limits.h](https://repo.or.cz/glibc.git/blob/HEAD:/include/limits.h)
+ 與一開始想的情況一樣,最小值是沒辦法取絕對值
+ 最小值取絕對值過程 `(0b1000...0 ^ (-1)) + 1 = 0b0111...1 + 1 = 0b1000...0` 又變回自己
:::info
**C99 Standard 6.5.7**
The result of E1 >> E2 is E1 right-shifted E2 bit positions. If E1 has an unsigned type or if E1 has a signed type and a nonnegative value, the value of the result is the integral part of the quotient of E1 / 2E2. ==If E1 has a signed type and a negative value, the resulting value is implementation-defined.==
:::
xor 真值表:
| $x$ | $y$ |$x \oplus y$|
|-- |-- |--|
| 0 | 0 | 0|
| 0 | 1 | 1|
| 1 | 0 | 1|
| 1 | 1 | 0|
考慮以下兩種情況:
1. $x > 0$
則 y = 00....000 ( 64 bit )
則 x ^ y = x
( $\because$不管 x 是0或1,跟0作 xor 運算結果都不會改變 )
而後面減 y 也不會變
$\therefore$ $x = x$
2. $x < 0$
則 y = 11....111 ( 64 bit )
則 x ^ y = $\overline x$
( 從真值表可看得出來 )
後面減掉 y 其實等同於 + 1
( $\because$ 負負得正 -(-1)=+1 )
$\therefore$ $x = -x$
規格書 6.5.7 中對於 shift operator 的規範。
> left shift operator
>
> The result of E1 << E2 is E1 left-shifted E2 bit positions; vacated bits are filled with zeros. If E1 has an unsigned type, the value of the result is E1 × 2E2, reduced modulo one more than the maximum value representable in the result type. If E1 has a signed type and nonnegative value, and E1 × 2E2 is representable in the result type, then that is the resulting value; otherwise, the behavior is undefined.
> right shift operator
>
> The result of E1 >> E2 is E1 right-shifted E2 bit positions. If E1 has an unsigned type or if E1 has a signed type and a nonnegative value, the value of the result is the integral part of the quotient of E1 / 2E2. If E1 has a signed type and a negative value, the resulting value is implementation-defined.
* 規格書中提到 right shift 和 left shift 對於 vacated bit 的填補行為不同,left shift 一律填補 `0`,但對於 right shift 的行為則要看實作而定。
* 更進一步在網路上搜尋相關討論,發現 shift operator 在邊界上的處理有以下 3 種策略
* [logical shift](https://en.wikipedia.org/wiki/Logical_shift)
超出邊界的位元數,會被捨棄,反之空缺的位元數會被以 `0` 填補。
* ones shift
和 logical shift 相對應,一樣捨棄超出之位元數,但以 `1` 填補。
* [arithmetic shift](https://en.wikipedia.org/wiki/Arithmetic_shift)
這類填補策略則介於上述二者之間,根據狀況決定如何填補,而這次題目中,就是善用這個策略使得絕對值的計算過程中避開了 branch prediction 。

上圖取自 Wikipedia 對於 arithmetic shift 的描述,從圖中可以看到右移過後的 `MSB'` 是根據右移前的 `MSB` 所決定,這也就是為何當 x 為負值時,y 會被以 `1` 填滿的原因。
* 根據[三一律](https://zh.wikipedia.org/wiki/%E4%B8%89%E5%88%86%E5%BE%8B),在接下來的運算中分成三個狀況討論
* x > 0
* y 在右移過後會是 `0x0`
* `x ^ y` 的結果依然是 x 本身
* 故 `(x ^ y) - y` 本質上來說就是 `x - 0` ,x 若為正值則經過上述運算後依然為自己本身
* x = 0
* y 在右移過後會是 `0x0`
* `x ^ y` 的結果還是 `0`
* `(x ^ y) - y` 會轉為 `0 - 0` 仍為 `0`
* x < 0
* 經過 arithmetic shift 後, y 會變成 `0xffffffffffffffff`
* `x ^ y` 的結果會是 `~x`
* `(x ^ y) - y` 和 `~x - y` 等價,而此時 `y` 所表示的值就是 `-1` ,也和 `~x - (-1)` 等價,而 `~x + 1` 正是 two's compliment 的定義
* 經過上述運算後,`x` 被轉為 `-x`
---
C 語言規格書:
> **C99 Standard (§ 6.5.7) Bitwise shift operators**
The result of E1 << E2 is E1 left-shifted E2 bit positions; vacated bits are filled with zeros. If E1 has an unsigned type, the value of the result is E1 × 2^E2^, reduced modulo one more than the maximum value representable in the result type. **If E1 has a signed type and nonnegative value, and E1 × 2^E2^ is representable in the result type, then that is the resulting value; otherwise, the behavior is undefined.**
> **C99 Standard (§ 6.5.7) Bitwise shift operators**
The result of E1 >> E2 is E1 right-shifted E2 bit positions. If E1 has an unsigned type or if E1 has a signed type and a nonnegative value, the value of the result is the integral part of the quotient of E1 / 2^E2^. **If E1 has a signed type and a negative value, the resulting value is implementation-defined.**
可以知道在`E1`在 signed type 的時候,若`E1`為非負,`E1`左移與右移`E2`個位元的結果會等同於 E1 x 2^E2^ 以及 E1 / 2^E2^;但是當`E1`為負數時,左移是一個 undefined behavior,右移則是 implementation-defind。
既然是 implementation-defined,那就來測試一下吧,使用 64 位元的有號整數來觀察:
```cpp
int main() {
int64_t m = 0x8000000000000300;
int64_t n = 0x0000000000000300;
}
```
開啟好用的 gdb 模式,雖然將負數左移是 undefined behavior,不過基於好奇心還是來看一下左移會發生什麼事:
```bash
(gdb) p/t m
$1 = 1000000000000000000000000000000000000000000000000000001100000000
(gdb) p/t m << 1
$2 = 11000000000 # 前方的 0 被省略了
(gdb) p/t m << 2
$3 = 110000000000 # 前方的 0 被省略了
```
可以看到左移的動作直接把`m`當作 unsigned type 來處理,無視最左方的 sign bit,將整個數進行位移。
接下來觀察右移的情形:
```shell
(gdb) p/t m
$4 = 1000000000000000000000000000000000000000000000000000001100000000
(gdb) p/t m >> 1
$5 = 1100000000000000000000000000000000000000000000000000000110000000
(gdb) p/t m >> 2
$6 = 1110000000000000000000000000000000000000000000000000000011000000
```
看起來也是直接將`m`當作 unsigned type 進行處理,不過會有 sign extension 的動作,將左方的 bit 補上 1。
接著觀察將負數`m`往右移 63 個位元的時候得出的結果所有的 bit 都會是 1。
```shell
(gdb) p/t m >> 63
$7 = 1111111111111111111111111111111111111111111111111111111111111111
```
再來觀察非負的數`n`往右移 63 個位元時得出的結果所有的 bit 都是 0。
```bash
(gdb) p/t n >> 63
$8 = 0
```
在此可以推測程式碼第一行應為:
```c
int64_t y = x >> (64 - 1);
```
我們的目的是要將負數進行二補數運算,而非負數則維持不變。
所以仔細觀察一下,當`A3`為`^`時,
```bash
(gdb) p/t m
$9 = 1000000000000000000000000000000000000000000000000000001100000000
(gdb) p/t m ^ (m >> 63)
$10 = 111111111111111111111111111111111111111111111111111110011111111
# $10 最前方的 0 被省略,所以才會少一個 bit
```
對齊一下比較好觀察,可以發現這不就是一補數的計算嗎:
```bash
1000000000000000000000000000000000000000000000000000001100000000 # x
0111111111111111111111111111111111111111111111111111110011111111 # x ^ y
```
計算式為`(x ^ y) - y`,因此還需要再減掉一次`y`,`y`的值是`0xffffffffffffffff`,在二補數表示法中代表 -1,不就是加一嗎?所以`(x ^ y) - y`在`x`是負數的時候就是做二補數啊!
```bash
(gdb) p/t (int64_t)-1
$11 = 1111111111111111111111111111111111111111111111111111111111111111
(gdb) p/x (int64_t)-1
$12 = 0xffffffffffffffff
```
那麼當`x`是非負整數時的情況呢?`y`的值是`0x0000000000000000`,`x ^ y`的結果仍然是`x`,`x - y`的結果也依舊是`x`。
```bash
(gdb) p/t n
$13 = 1100000000
(gdb) p/t n >> 63
$14 = 0
(gdb) p/t n ^ (n >> 63)
$15 = 1100000000
(gdb) p/t n ^ (n >> 63) - (n >> 63)
$16 = 1100000000
```
真是太神奇了!這段程式碼在`x`是非負整數時計算結果維持不變,而在`x`是負整數的時候卻進行了二補數的運算!
```c=
#include <stdint.h>
int64_t abs64(int64_t x) {
int64_t y = x >> (64 - 1);
return (x ^ y) - y;
}
```
### 延伸問題
64-bit的二補數表示法可表達的範圍為 -2^63^~2^62^-1,因此有可能產生 Overflow 的值只有 -2^63^,因為沒有對應的正數可以表示。
寫個程式測試需要多少時間能夠檢查完所有的數:
```cpp
#define the_abs(n) ((n) < 0 ? (-n) : (n))
double test(int64_t base, int64_t length) {
clock_t begin = clock();
int64_t i;
for (i = base; i < length; i++)
assert(abs64(i) == the_abs(i));
clock_t end = clock();
double time_spent = (double)(end - begin) / CLOCKS_PER_SEC;
return time_spent;
}
void a_test(int64_t b, int64_t l) {
double time_spent = test(b, l);
printf("%f seconds\n", time_spent);
}
int main() {
int64_t b = -10000;
int64_t l = 1;
for (int i = 0; i < 7; i++) {
a_test(b, l);
b *= 10;
}
}
```
```shell
0.000050 seconds # 1e4 筆資料
0.000473 seconds
0.004556 seconds
0.042300 seconds
0.341621 seconds
3.393501 seconds # 1e9 筆資料
34.005079 seconds # 1e10 筆資料
```
可以看到資料筆數與執行時間呈線性增長,10 億筆資料約需 3.4 秒執行,100 億筆資料約需 34 秒執行。
而 `int64_t` 的範圍為 -9,223,372,036,854,775,808 到 9,223,372,036,854,775,807,總共 18,446,744,073,709,551,616 筆資料,是 100 億的 1844674407 倍,因此執行時間預估需要 62718929838 秒。
```python
Python 3.7.0
>>> (int)(2**64 / 1e10)
1844674407
>>> (int)(2**64 / 1e10) * 34
62718929838
```
將[秒數轉換成年](https://www.calculateme.com/time/seconds/to-years/),大概需要 1,987 年才能夠檢查完所有的資料。
---
安裝 [cbmc](https://www.cprover.org/cbmc/)
```shell
$ sudo apt install cbmc
```
給定以下 `abs.c`
```cpp
#include <stdlib.h>
#include <stdint.h>
int64_t abs(int64_t x) {
int64_t y = x;
if (x < 0)
y = -x;
return y;
}
```
輸入以下命列:
```shell
$ cbmc abs.c --function abs --signed-overflow-check
```
預期可得以下輸出:
```
SAT checker: instance is SATISFIABLE
Runtime decision procedure: 0.001s
** Results:
[abs.overflow.1] arithmetic overflow on signed unary minus in -x: FAILURE
** 1 of 1 failed (1 iteration)
VERIFICATION FAILED
```
參考 [The CProver Suite of Verification Tools](https://svn.cprover.org/wiki/lib/exe/fetch.php?media=tutorial-slides1.pdf)
> Page 22-32
[形式化驗證與 cbmc](https://hackmd.io/s/Hk4lYmzkf)
---
###### Note
:::info
cbmc uses SSA form combines with SAT checker to verify program
:::
```c
root:~/ # cat test.c && goto-cc test.c -o test.goto && goto-instrument --dump-c test.goto
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
int main(void){
int m = INT_MIN;
printf("%d\n", abs(m));
return 0;
}
Reading GOTO program from `test.goto'
// abs
// file /usr/include/stdlib.h line 837
extern signed int abs(signed int);
// printf
// file /usr/include/stdio.h line 318
extern signed int printf(const char *, ...);
// main
// file test.c line 5
signed int main(void)
{
signed int m=-0x7FFFFFFF - 1;
signed int return_value_abs$1=abs(m);
printf("%d\n", return_value_abs$1);
return 0;
}
```
```c
#FILE: abs.c
#include <stdlib.h>
#include <stdint.h>
int64_t abs_test(int64_t x){
int64_t mask = x >> (64 - 1);
int64_t r = (x ^ mask);
r = r - mask;
return r;
}
```
:::info
節錄 `cbmc abs.c --function abs_test --signed-overflow-check --program-only`
:::
```c
// 1
// 2 file abs.c line 4
// 3 file abs.c line 4
// 3 file abs.c line 4
// 3 file abs.c line 4
(21) x!0@1#1 == x!0#1
// 22 file abs.c line 5 function abs_test
// 23 file abs.c line 5 function abs_test
(22) ASSERT(!overflow("-", signed int, 64, 1))
// 24 file abs.c line 5 function abs_test
(23) mask!0@1#2 == x!0@1#1 >> 63
// 25 file abs.c line 6 function abs_test
// 26 file abs.c line 6 function abs_test
(24) r!0@1#2 == (mask!0@1#2 ^ x!0@1#1)
// 27 file abs.c line 7 function abs_test
(25) ASSERT(!overflow("-", signed long int, r!0@1#2, mask!0@1#2))
// 28 file abs.c line 7 function abs_test
(26) r!0@1#3 == r!0@1#2 + -mask!0@1#2
// 29 file abs.c line 8 function abs_test
(27) abs_test#return_value!0#1 == r!0@1#3
// 32 file abs.c line 9 function abs_test
// 4 file abs.c line 4
(28) return'!0#1 == abs_test#return_value!0#1
// 6 file abs.c line 4
// 8
```
---
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet