---
tags: linux2022
---
# 2022q1 Homework1 (quiz1)
contributed by < `MicahDoo` >
> [題目](https://hackmd.io/@sysprog/linux2022-quiz1)
## 測驗 1
First, we zoom in on the function where we need to fill in the blanks:
```c
void map_add(map_t *map, int key, void *data){...}
```
### Line-by-line Trace
```c
struct hash_key *kn = find_key(map, key);
if (kn)
return;
```
:arrow_up: Return if key already exists.
```c
kn = malloc(sizeof(struct hash_key));
kn->key = key, kn->data = data;
```
:arrow_up: Create a node to be added to the map.
```c
struct hlist_head *h = &map->ht[hash(key, map->bits)];
```
:arrow_up: Locate the appropriate map entry/bucket 'hlist_head *h' (the list heads in an array) with the hash value generated with `hash()` using hash_key.
```c
struct hlist_node *n = &kn->node, *first = h->first;
```
:arrow_up: `n` points to the list node contained in the hash_key node. (`&` allows us to use the `->` operator)
`first` is the first node in the "bucket list" (no pun intended :smirk:), `NULL` if bucket is empty.
:thinking_face: After that, we might have one of the following two configurations: :point_down:
```graphviz
digraph table
{
labelloc="t";
label="Bucket Empty";
rankdir="LR"
layout=dot
splines = true;
node [shape=plaintext]
head [label=<<TABLE BORDER="0" CELLBORDER="1" CELLSPACING="0">
<TR><TD PORT="c" BGCOLOR="gray"> hlist_head [] </TD></TR>
<TR><TD PORT="e">⋮</TD></TR>
<TR><TD PORT="entry"> hlist_head.first </TD></TR>
<TR><TD PORT="f">⋮</TD></TR>
</TABLE>>];
new [label=<<TABLE BORDER="0" CELLSPACING="-1" CELLBORDER="0">
<TR><TD BGCOLOR="lightgray"> new container </TD></TR>
<TR><TD BGCOLOR="lightgray" ><TABLE BORDER="0" CELLBORDER="1" CELLSPACING="0">
<TR><TD PORT="name" BGCOLOR="gray" colspan="2">hlist_node</TD></TR>
<TR>
<TD PORT="pprev" BGCOLOR="white" >pprev</TD>
<TD PORT="next" BGCOLOR="white" >next</TD>
</TR>
</TABLE></TD></TR>
</TABLE>>];
NULL
head:entry -> NULL
NULL -> new [color="invis"]
{rank=same; NULL; first[fontcolor="purple"]}
first->NULL [color="purple"]
{rank=same; n [fontcolor="purple"]; new}
n->new:name:nw [color="purple"]
{rank="same"; h [fontcolor="purple"]; head}
h->head:entry:nw [color="purple"]
}
```
```graphviz
digraph table
{
labelloc="t";
label="Bucket not Empty";
splines = true;
rankdir="LR"
layout=dot
node [shape=plaintext]
head [label=<<TABLE BORDER="0" CELLBORDER="1" CELLSPACING="0">
<TR><TD PORT="c" BGCOLOR="gray"> hlist_head [] </TD></TR>
<TR><TD PORT="e">⋮</TD></TR>
<TR><TD PORT="entry"> hlist_head.first </TD></TR>
<TR><TD PORT="f">⋮</TD></TR>
</TABLE>>];
old [label=<<TABLE BORDER="0" CELLSPACING="-1" CELLBORDER="0">
<TR><TD BGCOLOR="lightgray"> container </TD></TR>
<TR><TD BGCOLOR="lightgray" ><TABLE BORDER="0" CELLBORDER="1" CELLSPACING="0">
<TR><TD PORT="name" BGCOLOR="gray" colspan="2">hlist_node</TD></TR>
<TR>
<TD PORT="pprev" BGCOLOR="white" >pprev</TD>
<TD PORT="next" BGCOLOR="white" >next</TD>
</TR>
</TABLE></TD></TR>
</TABLE>>];
new [label=<<TABLE BORDER="0" CELLSPACING="-1" CELLBORDER="0">
<TR><TD BGCOLOR="lightgray"> new container </TD></TR>
<TR><TD BGCOLOR="lightgray" ><TABLE BORDER="0" CELLBORDER="1" CELLSPACING="0">
<TR><TD PORT="name" BGCOLOR="gray" colspan="2">hlist_node</TD></TR>
<TR>
<TD PORT="pprev" BGCOLOR="white" >pprev</TD>
<TD PORT="next" BGCOLOR="white" >next</TD>
</TR>
</TABLE></TD></TR>
</TABLE>>];
NULL
old:pprev:s -> head:entry:se [style="dashed" color=""]
head:entry -> old:name
old:next -> "..." -> NULL
"..." -> old:next:se [style="dashed"]
old->new [color = "invis"]
{rank=same; old; first[fontcolor="purple"]}
first->old:name:nw [color="purple"]
{rank=same; n [fontcolor="purple"]; new}
n->new:name:nw [color="purple"]
{rank="same"; h [fontcolor="purple"]; head}
h->head:entry:nw [color="purple"]
}
```
```c
AAA;
if (first)
first->pprev = &n->next;
```
:arrow_up: If the bucket isn't empty, attach the first node to the new node by making `first->prev` point to the pointer to the new node `n`'s `next` variable: :point_down:
```graphviz
digraph table
{
labelloc="t";
label="Bucket not Empty";
rankdir="LR"
layout=dot
splines = true;
node [shape=plaintext]
head [label=<<TABLE BORDER="0" CELLBORDER="1" CELLSPACING="0">
<TR><TD PORT="c" BGCOLOR="gray"> hlist_head [] </TD></TR>
<TR><TD PORT="e">⋮</TD></TR>
<TR><TD PORT="entry"> hlist_head.first </TD></TR>
<TR><TD PORT="f">⋮</TD></TR>
</TABLE>>];
old [label=<<TABLE BORDER="0" CELLSPACING="-1" CELLBORDER="0">
<TR><TD BGCOLOR="lightgray"> container </TD></TR>
<TR><TD BGCOLOR="lightgray" ><TABLE BORDER="0" CELLBORDER="1" CELLSPACING="0">
<TR><TD PORT="name" BGCOLOR="gray" colspan="2">hlist_node</TD></TR>
<TR>
<TD PORT="pprev" BGCOLOR="white" >pprev</TD>
<TD PORT="next" BGCOLOR="white" >next</TD>
</TR>
</TABLE></TD></TR>
</TABLE>>];
new [label=<<TABLE BORDER="0" CELLSPACING="-1" CELLBORDER="0">
<TR><TD BGCOLOR="lightgray"> new container </TD></TR>
<TR><TD BGCOLOR="lightgray" ><TABLE BORDER="0" CELLBORDER="1" CELLSPACING="0">
<TR><TD PORT="name" BGCOLOR="gray" colspan="2">hlist_node</TD></TR>
<TR>
<TD PORT="pprev" BGCOLOR="white" >pprev</TD>
<TD PORT="next" BGCOLOR="white" >next</TD>
</TR>
</TABLE></TD></TR>
</TABLE>>];
NULL
old:pprev:s -> new:next:es [style="dashed" color="red"]
old:next -> "..." -> NULL
"..." -> old:next:se [style="dashed"]
new:next -> old:name [color = "invis"]
new:pprev:s -> head:entry [style="dashed" color = "invis"]
head:entry -> new:name [color = "invis"]
new:next -> old:name [color = "invis"]
head:entry:ne -> old:name:nw
{rank=same; old; first[fontcolor="purple"]}
first->old:name:ne [color="purple"]
n->new:name [color="purple"]
h->head:entry:w [color="purple"]
subgraph clustersubs {
label=""
color="invis"
head
new
h
n
{rank=same; new; n [fontcolor="purple"];}
{rank="same"; h [fontcolor="purple"]; head}
}
}
```
```c
h->first = n;
BBB;
```
:arrow_up: `h->first` points to the new first node: :point_down:
```graphviz
digraph table
{
labelloc="t";
label="Bucket Empty";
rankdir="LR"
layout=dot
node [shape=plaintext]
head [label=<<TABLE BORDER="0" CELLBORDER="1" CELLSPACING="0">
<TR><TD PORT="c" BGCOLOR="gray"> hlist_head [] </TD></TR>
<TR><TD PORT="e">⋮</TD></TR>
<TR><TD PORT="entry"> hlist_head.first </TD></TR>
<TR><TD PORT="f">⋮</TD></TR>
</TABLE>>];
new [label=<<TABLE BORDER="0" CELLSPACING="-1" CELLBORDER="0">
<TR><TD BGCOLOR="lightgray"> new container </TD></TR>
<TR><TD BGCOLOR="lightgray" ><TABLE BORDER="0" CELLBORDER="1" CELLSPACING="0">
<TR><TD PORT="name" BGCOLOR="gray" colspan="2">hlist_node</TD></TR>
<TR>
<TD PORT="pprev" BGCOLOR="white" >pprev</TD>
<TD PORT="next" BGCOLOR="white" >next</TD>
</TR>
</TABLE></TD></TR>
</TABLE>>];
NULL
head:entry:ne -> NULL
head:entry -> new:name [color="red"]
new:pprev -> head:entry [style="dashed" color="invis"]
NULL -> new [color="invis"]
new:next->NULL [color="invis"]
{rank=same; NULL; first[fontcolor="purple"]}
first->NULL [color="purple"]
{rank=same; n [fontcolor="purple"]; new}
n->new:name:ne [color="purple"]
{rank="same"; h [fontcolor="purple"]; head}
h->head:entry:nw [color="purple"]
}
```
```graphviz
digraph table
{
labelloc="t";
label="Bucket not Empty";
rankdir="LR"
layout=dot
splines = true;
node [shape=plaintext]
head [label=<<TABLE BORDER="0" CELLBORDER="1" CELLSPACING="0">
<TR><TD PORT="c" BGCOLOR="gray"> hlist_head [] </TD></TR>
<TR><TD PORT="e">⋮</TD></TR>
<TR><TD PORT="entry"> hlist_head.first </TD></TR>
<TR><TD PORT="f">⋮</TD></TR>
</TABLE>>];
old [label=<<TABLE BORDER="0" CELLSPACING="-1" CELLBORDER="0">
<TR><TD BGCOLOR="lightgray"> container </TD></TR>
<TR><TD BGCOLOR="lightgray" ><TABLE BORDER="0" CELLBORDER="1" CELLSPACING="0">
<TR><TD PORT="name" BGCOLOR="gray" colspan="2">hlist_node</TD></TR>
<TR>
<TD PORT="pprev" BGCOLOR="white" >pprev</TD>
<TD PORT="next" BGCOLOR="white" >next</TD>
</TR>
</TABLE></TD></TR>
</TABLE>>];
new [label=<<TABLE BORDER="0" CELLSPACING="-1" CELLBORDER="0">
<TR><TD BGCOLOR="lightgray"> new container </TD></TR>
<TR><TD BGCOLOR="lightgray" ><TABLE BORDER="0" CELLBORDER="1" CELLSPACING="0">
<TR><TD PORT="name" BGCOLOR="gray" colspan="2">hlist_node</TD></TR>
<TR>
<TD PORT="pprev" BGCOLOR="white" >pprev</TD>
<TD PORT="next" BGCOLOR="white" >next</TD>
</TR>
</TABLE></TD></TR>
</TABLE>>];
NULL
old:pprev:s -> new:next:es [style="dashed"]
old:next -> "..." -> NULL
"..." -> old:next:se [style="dashed"]
new:next -> old:name [color = "invis"]
new:pprev -> head:entry [style="dashed" color = "invis"]
head:entry -> new:name [color = "red"]
new:next:ne -> old:name [color = "invis"]
head:entry:ne -> old:name
{rank=same; old; first[fontcolor="purple"]}
first->old:name:nw [color="purple"]
n->new:name:sw [color="purple"]
h->head:entry:w [color="purple"]
subgraph clustersubs {
label=""
color="invis"
head
new
h
n
{rank=same; new; n [fontcolor="purple"];}
{rank="same"; h [fontcolor="purple"]; head}
}
}
```
From the graphs below we can easily see the missing links (in turquoise): :point_down:
```graphviz
digraph table
{
labelloc="t";
label="Bucket Empty";
rankdir="LR"
layout=dot
splines = true
node [shape=plaintext]
head [label=<<TABLE BORDER="0" CELLBORDER="1" CELLSPACING="0">
<TR><TD PORT="c" BGCOLOR="gray"> hlist_head [] </TD></TR>
<TR><TD PORT="e">⋮</TD></TR>
<TR><TD PORT="entry"> hlist_head.first </TD></TR>
<TR><TD PORT="f">⋮</TD></TR>
</TABLE>>];
new [label=<<TABLE BORDER="0" CELLSPACING="-1" CELLBORDER="0">
<TR><TD BGCOLOR="lightgray"> new container </TD></TR>
<TR><TD BGCOLOR="lightgray" ><TABLE BORDER="0" CELLBORDER="1" CELLSPACING="0">
<TR><TD PORT="name" BGCOLOR="gray" colspan="2">hlist_node</TD></TR>
<TR>
<TD PORT="pprev" BGCOLOR="white" >pprev</TD>
<TD PORT="next" BGCOLOR="white" >next</TD>
</TR>
</TABLE></TD></TR>
</TABLE>>];
head:entry -> new:name
new:pprev:s -> head:entry:se [style="dashed" color="turquoise"]
new:next->NULL [color="turquoise"]
{rank=same; NULL; first[fontcolor="purple"]}
first->NULL [color="purple"]
{rank=same; n [fontcolor="purple"]; new}
n->new:name:nw [color="purple"]
{rank="same"; h [fontcolor="purple"]; head}
h->head:entry:w [color="purple"]
}
```
```graphviz
digraph table {
rankdir="LR"
layout=dot
labelloc="t";
label="Bucket not Empty";
splines = true;
node [shape=plaintext]
head [label=<<TABLE BORDER="0" CELLBORDER="1" CELLSPACING="0">
<TR><TD PORT="c" BGCOLOR="gray">hlist_head []</TD></TR>
<TR><TD PORT="e">⋮</TD></TR>
<TR><TD PORT="entry"> hlist_head.first </TD></TR>
<TR><TD PORT="f">⋮</TD></TR>
</TABLE>>];
old [label=<<TABLE BORDER="0" CELLSPACING="-1" CELLBORDER="0">
<TR><TD BGCOLOR="lightgray"> container </TD></TR>
<TR><TD BGCOLOR="lightgray" ><TABLE BORDER="0" CELLBORDER="1" CELLSPACING="0">
<TR><TD PORT="name" BGCOLOR="gray" colspan="2">hlist_node</TD></TR>
<TR>
<TD PORT="pprev" BGCOLOR="white" >pprev</TD>
<TD PORT="next" BGCOLOR="white" >next</TD>
</TR>
</TABLE></TD></TR>
</TABLE>>];
new [label=<<TABLE BORDER="0" CELLSPACING="-1" CELLBORDER="0">
<TR><TD BGCOLOR="lightgray"> new container </TD></TR>
<TR><TD BGCOLOR="lightgray" ><TABLE BORDER="0" CELLBORDER="1" CELLSPACING="0">
<TR><TD PORT="name" BGCOLOR="gray" colspan="2">hlist_node</TD></TR>
<TR>
<TD PORT="pprev" BGCOLOR="white" >pprev</TD>
<TD PORT="next" BGCOLOR="white" >next</TD>
</TR>
</TABLE></TD></TR>
</TABLE>>];
NULL
{rank=same; first; old}
{rank=same; n; new}
head:entry -> new:name;
new:pprev:s -> head:entry:se [style="dashed" color="turquoise"];
new:next -> old:name [color="turquoise"];
old:pprev:s -> new:next:se [style="dashed"];
old:next -> "..."
"..." -> old:next:se [style="dashed"]
"..."->NULL
{rank=same; old; first[fontcolor="purple"]}
first->old:name:nw [color="purple"]
{rank=same; n [fontcolor="purple"]; new}
n->new:name:nw [color="purple"]
{rank="same"; h [fontcolor="purple"]; head}
h->head:entry:w [color="purple"]
}
```
### :writing_hand: Conclusions
AAA: `n->next = first`
BBB: `n->pprev = &h->first`
Fixed Code:
```c
void map_add(map_t *map, int key, void *data)
{
struct hash_key *kn = find_key(map, key);
if (kn)
return;
kn = malloc(sizeof(struct hash_key));
kn->key = key, kn->data = data;
struct hlist_head *h = &map->ht[hash(key, map->bits)];
struct hlist_node *n = &kn->node, *first = h->first;
n->next = first;
if (first)
first->pprev = &n->next;
h->first = n;
n->pprev = &h->first;
}
```
:::success
:pencil: **Can I swap AAA with BBB?**
:heavy_check_mark: Yes, because none of the four variables in AAA and BBB are modified or have their value accessed in between AAA and BBB.
:warning: `n->next` is accessed in between, but only the "address" is accessed, not the value.
:::
## 測驗 1 延伸問題 Additional Problems
### 1. Explain how the entire code works.
#### Hash Table Initialization
```c
map_t *map_init(int bits) {
map_t *map = malloc(sizeof(map_t));
if (!map)
return NULL;
map->bits = bits;
map->ht = malloc(sizeof(struct hlist_head) * MAP_HASH_SIZE(map->bits));
if (map->ht) {
for (int i = 0; i < MAP_HASH_SIZE(map->bits); i++)
(map->ht)[i].first = NULL;
} else {
free(map);
map = NULL;
}
return map;
}
```
:::warning
TODO
:::
### 2-1. Study this [Linux Kernel Source Code] in this link [include/linux/hashtable.h](https://github.com/torvalds/linux/blob/master/include/linux/hashtable.h) and its supporting [document](https://kernelnewbies.org/FAQ/Hashtables), and explain its hash table design and implementation.
:::warning
TODO
:::
### 2-2. What is `GOLDEN_RATIO_PRIME` used for in [tools/include/linux/hash.h](https://github.com/torvalds/linux/blob/master/tools/include/linux/hash.h)?
:::warning
TODO: 寫個中文的版本。
:::
#### :point_right: Efficient Distribution
In short, the golden ratio ensures an optimally **efficient distribution** of the hash values. That means it ensures that:
1. Every hash value has an equal chance of occurring.
2. The likelihood of a hash value being wasted is optimally low.
To illustrate that, I will stray off a bit and draw from real life examples.
#### :point_right: Real Life Example: Arranging Seeds
Let's start with a simple *Seed Distribution* problem:
Suppose I have a fairly big number of seeds I want to arrange. I start from the center and put the next seed to the right side of it:

Let's say I am a stupid robot. I can only remember *one rule* regarding how to decide the next location to place a seed:
> Make $n$ amount of a turn around the center from the current location. If a seed already occupies that location, push it out radially (along the radius).
Note: n should be constant throughout the process, or it wouldn't just be *one rule*.
Let's put n into [this program](https://www.geogebra.org/m/fh7jp5mq) and see what happens:
##### :thinking_face: e.g. $n = 1$ or $n = 0$
I make **one turn** before I put my next seed. That is, I turn 360° before I place the next seed.
(Trivially, $n = 0$, i.e. making no turn, will result in the same configuration.)

We can see that the seeds are arranged towards the same direction on a line.
That is not an efficient use of space.
##### :thinking_face: e.g. $n = \frac{1}{2}$

##### :thinking_face: e.g. $n = \frac{1}{3}$

##### :thinking_face: e.g. $n = \frac{2}{3}$

As with $n = \frac{1}{3}$, the resulting arrangement has 3 spokes.
##### :thinking_face: e.g. $n = \frac{1}{10}\wedge\frac{2}{10}...\frac{9}{10}...\frac{11}{10}$

This results in 10 spokes (輻條).
##### :thinking_face: e.g. $n = \frac{1}{2} + 0.0001$

We can see that it looks similar to the one with $n = \frac{1}{2}$ but with the spokes curved a little. That's because with every turn it nudges the turn a bit further than the $n=\frac{1}{2}$ one.
##### :thinking_face: $n = \frac{1}{2} + 0.001$

The spokes curve even more.
##### :thinking_face: $n = \frac{1}{2} + 0.01$

From the above experiments we can come up with a few observations:
1. When $n$ is a rational number, i.e. $n = \frac{p}{q}$, where $p$ and $q$ are relatively prime (i.e. $n$ is irreducible), *$q$ **straight** spokes* form, each growing radially away from the center.
* That is because the same angle repeats every $q$th times.
* The space between the spokes are wasted.
2. When $n is close to a rational number, i.e. $n \approx \frac{p}{q}$, where $p$ and $q$ are relatively prime, $q$ spokes form, only they appear to be curving towards the direction we make the turns. How much they curve depends on how far away $n$ is from the ratio $\frac{p}{q}$.
* That is because with every turn there is a small *shift* away from the original *straight spokes* that $n = \frac{p}{q}$ would have formed.
* Although the space between the spokes are still wasted, this results in a **better use of space** because the seeds don't have to be pushed out as much after each iteration.
:::info
When $n$ equals or is approximately a *rational number* $\frac{p}{q}$, the spoke pattern is clear, and the fair amount of space between the spokes are wasted.
:::
Let's turn our attention now to irrational numbers
##### :thinking_face: e.g. $n = \frac{1}{\pi}\approx0.31830988618$

1. Towards the center, 3 curved spokes form, as $0.31830988618\approx\frac{1}{3}=0.333333333$
2. As we go further away from the center, 22 spokes instead of 3 form, as $0.31830988618\approx\frac{7}{22}=0.31818181818$.
:::success
The reason the number of spokes changes has to do with the size of the seed. Towards the center it is not possible to stack 22 spokes in a circle without pushing a seed out.
In fact, if we continue putting more seeds and let the 22 spokes keep growing, the spokes' curvature increases and another spoke pattern occur (This time, the number of spokes would be 355.)
:::
##### :thinking_face: e.g. $n = \pi - 3 \approx0.14159265359$ (The same as $n = \pi$)

The spoke counts, outwards from the center:
1. 1
($0.14159265359\approx0.1\approx\frac{1}{10}$)
2. 7
($0.14159265359\approx0.14285714\approx\frac{1}{7}$)
3. 106
($0.14159265359\approx0.14150943\approx\frac{15}{106}$)
4. 113
($0.14159265359\approx0.14159292\approx\frac{16}{113}$)
:::danger
:exploding_head: It's hard to see the transition between 106 spokes and 113 spokes, so here is how we count them:

The reason it takes so much time to go from 7 spokes to 106 but so little from 106 to 113:
From 7, it takes a lot of time for the pattern to go far away enough from the center to have a circumference big enough to put all 106 spokes, but it doesn't take that much from 106 to 113 because the two numbers are really close. That's why we can see how the 106 spoke pattern meshes and merges into the 113 pattern quite nicely and there seems to be less space wasted around that area.
:::
:::info
Even with $\frac{1}{\pi}$ or $1-\pi$, which look pretty irrational, there is still quite some loss of space because it is easily approximated by a few rational numbers. That results in spoke patterns that grow outwards, which wastes space, especially if it remains for a while.

:bulb: We need an irrational number that is not easily approximated by any rational number. We don't want clear spoke patterns!
:::
To know how easily an irrational number can be approximated by rational numbers, we first have to know how to approximate an irrational number by rational numbers.
##### :writing_hand: Approximating Irrational Numbers by Continued Fraction
To approximate an irrational number by rational numbers, we call on the method of [Best Approximations by Continued Fractions](https://pi.math.cornell.edu/~gautam/ContinuedFractions.pdf#page16):
* $\pi \approx 3 + \frac{1}{7}=\frac{22}{7}$ → 7 spokes
* $\pi \approx 3 + \frac{1}{7 + \frac{1}{15}} = \frac{333}{106}$ → 106 spokes
* $\pi \approx 3 + \frac{1}{7 + \frac{1}{15+{\frac{1}{1}}}} = \frac{355}{113}$ → 113 spokes
* $\pi\approx 3 + \frac{1}{7 + \frac{1}{15+\frac{1}{1 + {\frac{1}{292}}}}} = \frac{103993}{33102}$ → 33102 spokes
Recall previous observations:
* Small spoke count jump e.g. 103 to 106:
* The previous spoke pattern (103 spokes) merges swiftly into the next pattern (116 spokes).
* Less waste of space.
* Big spoke count jump e.g 7 to 103:
* The previous spoke pattern (7 spokes) is allowed to grow outward for a good while before merging into the next pattern (103 spokes).
* More waste of space since the previous spoke pattern is allowed to spread out radially.
Going along the observations, we can predict a colossal waste of space as the pattern with $n = \pi$ grows from 113 spokes to 33102 spokes - the difference between the two numbers is simply too big!
Also, if we inspect their corresponding continued fractions closely, especially the red parts:
* $\pi \approx 3 + \frac{1}{7 + \color{red}{\frac{1}{15}}}$ → Big jump from 7 to 106.
* $\pi \approx 3 + \frac{1}{7 + \frac{1}{15+\color{red}{\frac{1}{1}}}}$ → Small jump from 106 to 113.
* $\pi\approx 3 + \frac{1}{7 + \frac{1}{15+\frac{1}{1 + \color{red}{\frac{1}{292}}}}}$ → HUGE jump from 113 to 33102.
We can observe that the closer the proper fraction we add to the denominator (red part) is to $\frac{1}{1}$, the smaller the increase is from the previous spoke count to the next.
Such observation tells us that a number that looks like this might be ideal:
* $n = 1 + \frac{1}{\color{turquoise}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+...}}}}}}}$
We can see that all the new fractions added to the denominator in each iteration are $\frac{1}{1}$.
Solve the equation for $n$:
* The blue part is effectively n repeating itself:
$n = 1+ \frac{1}{n}$
→ $n^2-n-1=0$
→ $(n-\frac{1}{2})^2=\frac{5}{4}$
→ $n - \frac{1}{2} = \pm\frac{\sqrt{5}}{2}$
→ $n = \frac{1\pm\sqrt{5}}{2}$
:::info
$n = \frac{1\pm\sqrt{5}}{2}$ is the **golden ratio**.
:::
Now, let's plug the given golden ratio into the spiral generator:
##### :thinking_face: e.g. $n = \frac{1+\sqrt{5}}{2}$ or $n = \frac{1}{\frac{1+\sqrt{5}}{2}} = -\frac{1-\sqrt{5}}{2}$

:::info
The golden ratio results in the prefect arrangement: efficient space use, even distributioin.
It's even hard to figure out how many spokes there are at a certain distance from the center because they seem to mix quite tightly and transitions so smoothly.
:::
Let's examine how the number of spokes changes arithmetically:
* $1 + \frac{1}{1}=\frac{2}{1}$ → 1 spoke
* $\frac{1}{1 + \frac{1}{1}} = \frac{3}{2}$ → 2 spokes
* $\frac{1}{1 + \frac{1}{1+{\frac{1}{1}}}} = \frac{5}{3}$ → 3 spokes
* $\frac{1}{1 + \frac{1}{1+\frac{1}{1 + {\frac{1}{1}}}}} = \frac{8}{5}$ → 5 spokes
* $\frac{1}{1 + \frac{1}{1+\frac{1}{1 + {\frac{1}{1+\frac{1}{1}}}}}} = \frac{13}{8}$ → 8 spokes
:::info
The number of spokes grows slowly.
In fact, it matches the **Fibonacci Sequence**.
That is why hashing using the golden ratio is called **Fibonacci Hashing**.
:::
#### Examples in Nature
:::warning
Seeds in the sunflower are arranged so as to take maximum advantage of the limited space.
The pattern looks exactly the same as the pattern we derived with the golden ratio above.

:::
:::success
A plant often grows in a way that spreads out its leaves to catch the most sunlight.
The golden ratio helps achieve that.
Plants tend to be fairly consistent when it comes to the angle between one leaf and the next. That angle, not surprisingly, is the same angle with which we arrange the seeds in the previous section.
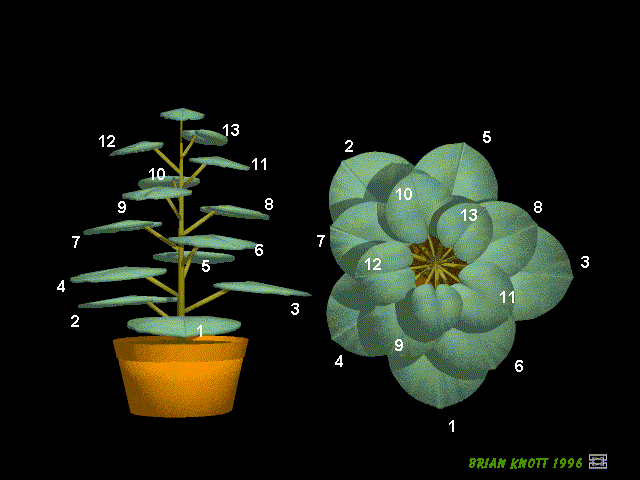
:::
> In fact, the golden ratio is often not only useful, but also inevitible in general. Watch this following video series by Vihart to find out:
[Doodling in Math: Spirals, Fibonacci, and Being a Plant [1 of 3]](https://www.youtube.com/watch?v=ahXIMUkSXX0)
{%youtube ahXIMUkSXX0 %}
[Doodling in Math: Spirals, Fibonacci, and Being a Plant [2 of 3]](https://www.youtube.com/watch?v=lOIP_Z_-0Hs)
{%youtube lOIP_Z_-0Hs %}
[Doodling in Math: Spirals, Fibonacci, and Being a Plant [3 of 3]](https://www.youtube.com/watch?v=14-NdQwKz9w)
{%youtube 14-NdQwKz9w %}
#### :point_right: Golden Ratio in Hashing
With that, we come back to why and how `GOLDEN_RATIO_PRIME` is used for hashing.
As shown in the above exploration, the golden ratio is perfect at taking input data and scattering them into efficiently distributed numbers:
* :inbox_tray: Input: the number of **golden ratio turns** to make from the original angle.
* :1234: Function: rotate the angle by **golden ratio** times 360 degrees. The angle resets itself at 360 degrees, i.e. if by calculation the next angle comes to $365.3$ degrees, it should be updated to $365.3-360 = 5.3$ degrees.
* :outbox_tray: Output: the new angle, which is perfectly scattered and never goes back to the original angle.
In computers, drawing a comparison between rotation and modular arithmetic, hence likening the key to the number of turns, the angle to the hash values, this would roughly be:
* :inbox_tray: Input: the key
* :1234: Function: multiply the key by **golden ratio** times 1. Then $modulo$ the result by one, i.e. retrieve only the fraction part. (Similar to resetting of the angle above.)
* :outbox_tray: Output: a fraction that never repeats itself.
In hashing, though, we often deal with **discrete integer values** based on the size of the hash table, so *the hash value must repeat itself at some point (the pigeonhole principle)*.
So here we make use of another property of the output:
* The **perfect scatter** property cascades quite well into the most significant bits of the fraction. For example, if we only look at, say, the first digit after decimal of the multiplication:
<!--ctrl cmd to swap two lines, cmd and change cursor to make multiple cursors-->
* $0.61803398875 \times 0 \text{ }\bmod 1 = 0.\color{red}000$
* $0.61803398875 \times 1 \text{ }\bmod 1 = 0.\color{red}618$
* $0.61803398875 \times 2 \text{ }\bmod 1 = 0.\color{red}236$
* $0.61803398875 \times 3 \text{ }\bmod 1 = 0.\color{red}854$
* $0.61803398875 \times 4 \text{ }\bmod 1 = 0.\color{red}472$
* $0.61803398875 \times 5 \text{ }\bmod 1 = 0.\color{red}090$
* $0.61803398875 \times 6 \text{ }\bmod 1 = 0.\color{red}708$
* $0.61803398875 \times 7 \text{ }\bmod 1 = 0.\color{red}326$
* $0.61803398875 \times 8 \text{ }\bmod 1 = 0.\color{red}944$
* $0.61803398875 \times 9 \text{ }\bmod 1 = 0.\color{red}562$
* $0.61803398875 \times 10 \bmod 1 = 0.\color{red}180$
* $0.61803398875 \times 11 \bmod 1 = 0.\color{red}798$
* $0.61803398875 \times 12 \bmod 1 = 0.\color{red}416$
* $0.61803398875 \times 13 \bmod 1 = 0.\color{red}034$
* $0.61803398875 \times 14 \bmod 1 = 0.\color{red}652$
* $0.61803398875 \times 15 \bmod 1 = 0.\color{red}270$
* $0.61803398875 \times 16 \bmod 1 = 0.\color{red}888$
* $0.61803398875 \times 17 \bmod 1 = 0.\color{red}506$
* $0.61803398875 \times 18 \bmod 1 = 0.\color{red}124$
* $0.61803398875 \times 19 \bmod 1 = 0.\color{red}742$
* $0.61803398875 \times 20 \bmod 1 = 0.\color{red}360$
* The digits go like this: 062840739517406285173: three 0's, one 9 and two each for 1-8. We can see that it's pretty evenly distributed. Even better is the fact that there seems to be no clear repeating pattern and the numbers don't go predictably like 1234567890 such as what we would see in modular hashing. That prevents a bad hash from happening if there happens to be a pattern in the keys, e.g. all the keys are multiples of ten:
* $0.61803398875 \times 10 \bmod 1 = 0.\color{red}180$
* $0.61803398875 \times 20 \bmod 1 = 0.\color{red}360$
* $0.61803398875 \times 30 \bmod 1 = 0.\color{red}541$
* $0.61803398875 \times 40 \bmod 1 = 0.\color{red}721$
* $0.61803398875 \times 50 \bmod 1 = 0.\color{red}901$
:::success
##### The higher digits/bits look more random than the lower digits/bits
The higher digits/bits (more significant digits/bits) are subject to carries from the lower digits/bits. In other words, changes in as far as the lowest digits/bits can propagate themselves to as far as the highest digits/bits. This sort of **chain reaction** can go infinitely far in some cases.
Imagine a series of multiplications:
* $0.\color{blue}{00001}\color{red}{00001} \times 1 \bmod 1 = 0.\color{blue}{00001}\color{red}{00001}$
* $0.\color{blue}{00001}\color{red}{00001} \times 2 \bmod 1 = 0.\color{blue}{00002}\color{red}{00002}$
* ...
* $0.\color{blue}{00001}\color{red}{00001} \times 99999 \bmod 1 = 0.\color{blue}{99999}\color{red}{99999}$
* $0.\color{blue}{00001}\color{red}{00001} \times 100000 \bmod 1 = 1.\color{blue}{00001}\color{red}{00000}$
* If we go on in the above fashion for long enough, it's easy to see that the red part repeats the pattern 00001 → ... → 99999 → 00000 → 00001 → ... again and again without fault. On the other hand, the blue part seems to follow the same pattern until the red part reaches 99999 and adding 1 to the rightmost digit contributes to a propagating carry towards the blue part. As a result, the blue part skips 00000 in the first cycle, then skips 00001 in the second cycle, then 00002 in the third, and so on, which happens each time the red part contributes a carry to the blue part. On the other hand, no matter what the blue part is, the red part repeats the same pattern, unaffected by its neighbor on the left.
* In short:
1. Higher digits/bits are affected by lower digits/bits, no matter how far away the latter are.
2. Lower digits/bits are never affected by higher digits/bits.
* That is why the higher digits/bits are preferred for hashing - they look more randomized because there are more factors at play than simply following a repeating pattern.
:::
With that in mind we change our function to something like this:
* Assume a hash table size of n.
* $\phi^{-1} = 0.618$
* :inbox_tray: Input: the key $k$.
* :1234: Function: $hash = \lfloor{(k \times \phi^{-1} \bmod 1) \times n}\rfloor$
* Multiply the key by **golden ratio** times 1. Then modulo the result by one, i.e. retrieve only the fraction part. Lastly, multiply the fraction by n, then take away the fraction part, leaving an integer.
* Since $0 < fraction \leq 1$, the result will be between 0 and n-1, as required to index into the hash table.
* :outbox_tray: Output: a hash value between 0 and n-1 to index into the hash table, its distribution is very even:
* It repeats itself on average every n times (on average, but rarely exactly), but doesn't show a clear pattern.
That is what we call the [Fibonacci Hashing](https://probablydance.com/2018/06/16/fibonacci-hashing-the-optimization-that-the-world-forgot-or-a-better-alternative-to-integer-modulo/).
#### :point_right: Linux Kernel Hashing
In fact, Linux Kernel implements a version of Fibonacci Hashing in [/include/hash.h](https://github.com/torvalds/linux/blob/master/tools/include/linux/hash.h):
##### define values
`GOLDEN_RATIO_32`: `0x61C88647 = 2654435769 (unsigned)` $= \frac{2^{32}}{\phi}$
`GOLDEN_RATIO_64`: `0x61C8864680B583EBull = 7.0460293E18 (unsigned)` $= \frac{2^{64}}{\phi}$
* ull = unsgined long long
* $\phi = 1.61803398875$
* `GOLDEN_RATIO_PRIME` can be either of them depending on the word length.
Both of them are the biggest unsigned number possible in their corresponding number of bits divided by the golden ratio.
:::success
Since $\frac{1}{\frac{1+\sqrt{5}}{2}} = -\frac{1-\sqrt{5}}{2}$ or $\frac{1}{1.61803398875} = 0.61803398875$, we can see multiplying by `GOLDEN_RATIO_xx` as multiplying by $2^{32/64} \times 0.61803398875$.
:point_right: Both $1.61803398875$ and $0.61803398875$ can be seen as the golden ratio here.
:::
```c
#if BITS_PER_LONG == 32
#define GOLDEN_RATIO_PRIME GOLDEN_RATIO_32
#define hash_long(val, bits) hash_32(val, bits)
#elif BITS_PER_LONG == 64
#define hash_long(val, bits) hash_64(val, bits)
#define GOLDEN_RATIO_PRIME GOLDEN_RATIO_64
#else
#error Wordsize not 32 or 64
#endif
#define GOLDEN_RATIO_32 0x61C88647
#define GOLDEN_RATIO_64 0x61C8864680B583EBull /* ull = unsigned long long */
```
##### Hashing in 32 bits
Notice the comment `/* High bits are more random, so use them. */`, which goes in line with our observation [above](#The-higher-digits/bits-look-more-random-than-the-lower-digits/bits).
```c
#ifndef HAVE_ARCH__HASH_32
#define __hash_32 __hash_32_generic
#endif
static inline u32 __hash_32_generic(u32 val)
{
return val * GOLDEN_RATIO_32;
}
static inline u32 hash_32(u32 val, unsigned int bits)
{
/* High bits are more random, so use them. */
return __hash_32(val) >> (32 - bits);
}
```
Following the code above, inlining functions when possible, a hashing in 32 bits in Linux is basically:
```
(val * GOLDEN_RATIO_32) >> (32 - bits);
```
Transform that into MathJax and let $\phi^{-1} = 0.61803398875$:
:-1: ${val} \times 2^{32} \times \phi^{-1} \div (\frac{2^{32}}{2^{bits}})$
...which is not entirely accurate because with integer type values, there are overflow and truncation:
:+1: $\lfloor ((({val} \times (2^{32} \times \phi^{-1})) \bmod 2^{32}) \div (\frac{2^{32}}{2^{bits}}) \rfloor$
Compare that to the hash formula we had above:
$hash = \lfloor{(k \times \phi^{-1} \bmod 1) \times n}\rfloor$
It might not be immediately clear that they are doing the same thing, so here is a short walkthrough:
Let's assume an integer word length of 8 bits (instead of 32 or 64) for simplicity.
$0.618033988 = 0.10011110$ in binary, to the 8th bits after the binary point.
```graphviz
digraph R {
rankdir=LR
node [shape=plaintext]
graph [ranksep="0", nodesep="0"];
bits[label=<
<TABLE BORDER="0" CELLBORDER="1" CELLSPACING = "0">
<TR>
<TD PORT="l8">0</TD>
<TD PORT="l7">0</TD>
<TD PORT="l6">0</TD>
<TD PORT="l5">0</TD>
<TD PORT="l4">0</TD>
<TD PORT="l3">0</TD>
<TD PORT="l2">0</TD>
<TD PORT="l1">0</TD>
<TD PORT=".">.</TD>
<TD PORT="r8">1</TD>
<TD PORT="r7">0</TD>
<TD PORT="r6">0</TD>
<TD PORT="r5">1</TD>
<TD PORT="r4">1</TD>
<TD PORT="r3">1</TD>
<TD PORT="r2">1</TD>
<TD PORT="r1">0</TD>
</TR>
</TABLE>>
]
}
```
Let's apply the following formula with the key $k = 5$ and the hash size $n = 2^4 = 16$
$hash = \lfloor{(key \times \phi^{-1} \bmod 1) \times n}\rfloor$
* $hash = \lfloor{(\color{red}{5 \times \phi^{-1}} \bmod 1) \times n}\rfloor$
```graphviz
digraph R {
rankdir=LR
node [shape=plaintext]
text [label="× 5" fontcolor="red"]
graph [ranksep="0", nodesep="0"];
splines = true
bits[label=<
<TABLE BORDER="0" CELLBORDER="1" CELLSPACING = "0">
<TR>
<TD PORT="l8">0</TD>
<TD PORT="l7">0</TD>
<TD PORT="l6">0</TD>
<TD PORT="l5">0</TD>
<TD PORT="l4">0</TD>
<TD PORT="l3">0</TD>
<TD PORT="l2"><font color="red">1</font></TD>
<TD PORT="l1"><font color="red">1</font></TD>
<TD PORT=".">.</TD>
<TD PORT="r8"><font color="red">0</font></TD>
<TD PORT="r7"><font color="red">0</font></TD>
<TD PORT="r6"><font color="red">0</font></TD>
<TD PORT="r5"><font color="red">1</font></TD>
<TD PORT="r4"><font color="red">0</font></TD>
<TD PORT="r3"><font color="red">1</font></TD>
<TD PORT="r2"><font color="red">1</font></TD>
<TD PORT="r1"><font color="red">0</font></TD>
</TR>
</TABLE>>
height = 0]
}
```
* $hash = \lfloor{(\color{blue}{5 \times \phi^{-1}} \color{red}{\bmod 1}) \times n}\rfloor$
```graphviz
digraph R {
rankdir=LR
node [shape=plaintext]
graph [ranksep="0", nodesep="0"];
splines = false
bits[label=<
<TABLE BORDER="0" CELLBORDER="1" CELLSPACING = "0">
<TR>
<TD PORT="l8">x</TD>
<TD PORT="l7">x</TD>
<TD PORT="l6">x</TD>
<TD PORT="l5">x</TD>
<TD PORT="l4">x</TD>
<TD PORT="l3">x</TD>
<TD PORT="l2"><font color="red">x</font></TD>
<TD PORT="l1"><font color="red">x</font></TD>
<TD PORT=".">.</TD>
<TD PORT="r8">0</TD>
<TD PORT="r7">0</TD>
<TD PORT="r6">0</TD>
<TD PORT="r5">1</TD>
<TD PORT="r4">0</TD>
<TD PORT="r3">1</TD>
<TD PORT="r2">1</TD>
<TD PORT="r1">0</TD>
</TR>
</TABLE>>
height = 0]
}
```
* $hash = \lfloor{\color{blue}{(5 \times \phi^{-1} {\bmod 1})} \color{red}{\times 16}}\rfloor$
```graphviz
digraph R {
rankdir=LR
node [shape=plaintext]
graph [ranksep="0", nodesep="0"];
text [label="← 4 bits" fontcolor="red"]
splines = false
bits[label=<
<TABLE BORDER="0" CELLBORDER="1" CELLSPACING = "0">
<TR>
<TD PORT="l8">x</TD>
<TD PORT="l7">x</TD>
<TD PORT="l6">x</TD>
<TD PORT="l5">x</TD>
<TD PORT="l4"><font color="red">0</font></TD>
<TD PORT="l3"><font color="red">0</font></TD>
<TD PORT="l2"><font color="red">0</font></TD>
<TD PORT="l1"><font color="red">1</font></TD>
<TD PORT=".">.</TD>
<TD PORT="r8"><font color="red">0</font></TD>
<TD PORT="r7"><font color="red">1</font></TD>
<TD PORT="r6"><font color="red">1</font></TD>
<TD PORT="r5"><font color="red">0</font></TD>
<TD PORT="r4">x</TD>
<TD PORT="r3">x</TD>
<TD PORT="r2">x</TD>
<TD PORT="r1">x</TD>
</TR>
</TABLE>>
height = 0]
}
```
* $hash = \color{red}{\lfloor}{\color{blue}{(5 \times \phi^{-1} {\bmod 1}) \times 16}}\color{red}{\rfloor}$
```graphviz
digraph R {
rankdir=LR
node [shape=plaintext]
graph [ranksep="0", nodesep="0"];
splines = false
bits[label=<
<TABLE BORDER="0" CELLBORDER="1" CELLSPACING = "0">
<TR>
<TD PORT="l8">x</TD>
<TD PORT="l7">x</TD>
<TD PORT="l6">x</TD>
<TD PORT="l5">x</TD>
<TD PORT="l4">0</TD>
<TD PORT="l3">0</TD>
<TD PORT="l2">0</TD>
<TD PORT="l1">1</TD>
<TD PORT=".">.</TD>
<TD PORT="r8"><font color="red">x</font></TD>
<TD PORT="r7"><font color="red">x</font></TD>
<TD PORT="r6"><font color="red">x</font></TD>
<TD PORT="r5"><font color="red">x</font></TD>
<TD PORT="r4">x</TD>
<TD PORT="r3">x</TD>
<TD PORT="r2">x</TD>
<TD PORT="r1">x</TD>
</TR>
</TABLE>>
height = 0]
}
```
Now we plug in the same values to the linux version of the formula:
* $\lfloor ((({key} \times (\color{red}{2^{8} \times \phi^{-1}}) \bmod 2^{8}) \div (\frac{2^{8}}{2^{bits}}) \rfloor$
```graphviz
digraph R {
rankdir=LR
node [shape=plaintext]
graph [ranksep="0", nodesep="0"];
text [label="← 8 bits" fontcolor="red"]
splines = false
bits[label=<
<TABLE BORDER="0" CELLBORDER="1" CELLSPACING = "0">
<TR>
<TD PORT="l16">x</TD>
<TD PORT="l15">x</TD>
<TD PORT="l14">x</TD>
<TD PORT="l13">x</TD>
<TD PORT="l12">x</TD>
<TD PORT="l11">x</TD>
<TD PORT="l10">x</TD>
<TD PORT="l9">x</TD>
<TD PORT="l8"><font color="red">1</font></TD>
<TD PORT="l7"><font color="red">0</font></TD>
<TD PORT="l6"><font color="red">0</font></TD>
<TD PORT="l5"><font color="red">1</font></TD>
<TD PORT="l4"><font color="red">1</font></TD>
<TD PORT="l3"><font color="red">1</font></TD>
<TD PORT="l2"><font color="red">1</font></TD>
<TD PORT="l1"><font color="red">0</font></TD>
<TD PORT=".">.</TD>
<TD PORT="r8">x</TD>
<TD PORT="r7">x</TD>
<TD PORT="r6">x</TD>
<TD PORT="r5">x</TD>
<TD PORT="r4">x</TD>
<TD PORT="r3">x</TD>
<TD PORT="r2">x</TD>
<TD PORT="r1">x</TD>
</TR>
</TABLE>>
height = 0]
}
```
* $\lfloor (((\color{red}{4 \times} \color{blue}{(2^{8} \times \phi^{-1})} \bmod 2^{8}) \div (\frac{2^{8}}{2^{bits}}) \rfloor$
```graphviz
digraph R {
rankdir=LR
node [shape=plaintext]
graph [ranksep="0", nodesep="0"];
text [label="× 5" fontcolor="red"]
splines = false
bits[label=<
<TABLE BORDER="0" CELLBORDER="1" CELLSPACING = "0">
<TR>
<TD PORT="l16">x</TD>
<TD PORT="l15">x</TD>
<TD PORT="l14">x</TD>
<TD PORT="l13">x</TD>
<TD PORT="l12">x</TD>
<TD PORT="l11">x</TD>
<TD PORT="l10"><font color="red">1</font></TD>
<TD PORT="l9"><font color="red">1</font></TD>
<TD PORT="l8"><font color="red">0</font></TD>
<TD PORT="l7"><font color="red">0</font></TD>
<TD PORT="l6"><font color="red">0</font></TD>
<TD PORT="l5"><font color="red">1</font></TD>
<TD PORT="l4"><font color="red">0</font></TD>
<TD PORT="l3"><font color="red">1</font></TD>
<TD PORT="l2"><font color="red">1</font></TD>
<TD PORT="l1"><font color="red">0</font></TD>
<TD PORT=".">.</TD>
<TD PORT="r8">x</TD>
<TD PORT="r7">x</TD>
<TD PORT="r6">x</TD>
<TD PORT="r5">x</TD>
<TD PORT="r4">x</TD>
<TD PORT="r3">x</TD>
<TD PORT="r2">x</TD>
<TD PORT="r1">x</TD>
</TR>
</TABLE>>
height = 0]
}
```
* $\lfloor ((\color{blue}{(4 \times {(2^{8} \times \phi^{-1})}} \color{red}{\bmod 2^{8}}) \div (\frac{2^{8}}{2^{bits}}) \rfloor$
```graphviz
digraph R {
rankdir=LR
node [shape=plaintext]
graph [ranksep="0", nodesep="0"];
text [label="overflow" fontcolor="red"]
splines = false
bits[label=<
<TABLE BORDER="0" CELLBORDER="1" CELLSPACING = "0">
<TR>
<TD PORT="l16">x</TD>
<TD PORT="l15">x</TD>
<TD PORT="l14">x</TD>
<TD PORT="l13">x</TD>
<TD PORT="l12">x</TD>
<TD PORT="l11">x</TD>
<TD PORT="l10"><font color="red">x</font></TD>
<TD PORT="l9"><font color="red">x</font></TD>
<TD PORT="l8">0</TD>
<TD PORT="l7">0</TD>
<TD PORT="l6">0</TD>
<TD PORT="l5">1</TD>
<TD PORT="l4">0</TD>
<TD PORT="l3">1</TD>
<TD PORT="l2">1</TD>
<TD PORT="l1">0</TD>
<TD PORT=".">.</TD>
<TD PORT="r8">x</TD>
<TD PORT="r7">x</TD>
<TD PORT="r6">x</TD>
<TD PORT="r5">x</TD>
<TD PORT="r4">x</TD>
<TD PORT="r3">x</TD>
<TD PORT="r2">x</TD>
<TD PORT="r1">x</TD>
</TR>
</TABLE>>
height = 0]
}
```
* $\lfloor (\color{blue}{((4 \times {(2^{8} \times \phi^{-1})}) \bmod 2^{8})} \color{red}{\div 2^{4}}) \rfloor$
```graphviz
digraph R {
rankdir=LR
node [shape=plaintext]
graph [ranksep="0", nodesep="0"];
text [label="→ shift back 8 bits then ← 4 bits\n leaves 4 bits on the left" fontcolor="red"]
splines = false
bits[label=<
<TABLE BORDER="0" CELLBORDER="1" CELLSPACING = "0">
<TR>
<TD PORT="l16">x</TD>
<TD PORT="l15">x</TD>
<TD PORT="l14">x</TD>
<TD PORT="l13">x</TD>
<TD PORT="l12">x</TD>
<TD PORT="l11">x</TD>
<TD PORT="l10">x</TD>
<TD PORT="l9">x</TD>
<TD PORT="l8">x</TD>
<TD PORT="l7">x</TD>
<TD PORT="l6">x</TD>
<TD PORT="l5">x</TD>
<TD PORT="l4"><font color="red">0</font></TD>
<TD PORT="l3"><font color="red">0</font></TD>
<TD PORT="l2"><font color="red">0</font></TD>
<TD PORT="l1"><font color="red">1</font></TD>
<TD PORT=".">.</TD>
<TD PORT="r8"><font color="red">0</font></TD>
<TD PORT="r7"><font color="red">1</font></TD>
<TD PORT="r6"><font color="red">1</font></TD>
<TD PORT="r5"><font color="red">0</font></TD>
<TD PORT="r4">x</TD>
<TD PORT="r3">x</TD>
<TD PORT="r2">x</TD>
<TD PORT="r1">x</TD>
</TR>
</TABLE>>
height = 0]
}
```
* $\color{red}\lfloor \color{blue}{({((4 \times {(2^{8} \times \phi^{-1})}) \bmod 2^{8})} \div 2^{4})} \color{red}\rfloor$
```graphviz
digraph R {
rankdir=LR
node [shape=plaintext]
graph [ranksep="0", nodesep="0"];
text [label="truncation" fontcolor="red"]
splines = false
bits[label=<
<TABLE BORDER="0" CELLBORDER="1" CELLSPACING = "0">
<TR>
<TD PORT="l16">x</TD>
<TD PORT="l15">x</TD>
<TD PORT="l14">x</TD>
<TD PORT="l13">x</TD>
<TD PORT="l12">x</TD>
<TD PORT="l11">x</TD>
<TD PORT="l10">x</TD>
<TD PORT="l9">x</TD>
<TD PORT="l8">x</TD>
<TD PORT="l7">x</TD>
<TD PORT="l6">x</TD>
<TD PORT="l5">x</TD>
<TD PORT="l4">0</TD>
<TD PORT="l3">0</TD>
<TD PORT="l2">0</TD>
<TD PORT="l1">1</TD>
<TD PORT=".">.</TD>
<TD PORT="r8"><font color="red">x</font></TD>
<TD PORT="r7"><font color="red">x</font></TD>
<TD PORT="r6">x</TD>
<TD PORT="r5">x</TD>
<TD PORT="r4">x</TD>
<TD PORT="r3">x</TD>
<TD PORT="r2">x</TD>
<TD PORT="r1">x</TD>
</TR>
</TABLE>>
height = 0]
}
```
...which is the same result!
The major difference between the normal version and the Linux version:
* The Linux version shifts the fraction part to the left first, does the calculation entirely on the left side of the binary point, then shifts it back.
:::info
The Linux version has a few advantages:
1. It does multiplication on `int` only, which is decidedly faster than `float` or `double` multiplications.
2. Modulo and floor operations are done automatically with overflow and truncation.
:::
##### 64-bit Version
Since very rarely does anyone need a hash function of more than $2^{32}$ in size, Linux does not have a hash function that maps a 64-bit hash key to a 64-bit hash value. ([Source](https://lwn.net/Articles/687494/))
Nevertheless, Linux does have a mechanism that maps a 64-bit hash key to a 32-bit hash value. Which is the function below:
```c
static __always_inline u32 hash_64_generic(u64 val, unsigned int bits)
{
#if BITS_PER_LONG == 64
/* 64x64-bit multiply is efficient on all 64-bit processors */
/* NOTICE: * comes before >> in precedence */
return val * GOLDEN_RATIO_64 >> (64 - bits);
#else
/* Hash 64 bits using only 32x32-bit multiply. */
return hash_32((u32)val ^ __hash_32(val >> 32), bits);
#endif
}
```
* When `BITS_PER_LONG == 64`, the function does the hashing normally in 64-bit operations but the result is returned in 32-bit integer, which means the left 32-bit half is discarded.
* When `BITS_PER_LONG == 32`, the function takes advantage of the fact that `XOR` causes no information loss:
* It shrinks the 64-bit hash key to a 32-bit one by first multiplying the left half of `val` by `GOLDEN_RATIO_64`, then performing `XOR` on the resulting value and the right half of `val`, before feeding it into the hash function.
:::warning
QUESTIONS TO RESOLVE:
- [ ] Why does it return a 32-bit number even if it has the ability to just return the 64-bit number?
- [ ] Does returning a `u64` value when the retrun type is `u32` raise an error? Or does the compiler do the conversion automatically?
- [ ] How can the function accept a `u64` value when `BITS_PER_LONG == 32`? What exactly does `BITS_PER_LONG == 32` mean?
:::
#### :point_right: Takeaway:
> The golden ratio is a nice way to randomly spread out, or efficiently distribute something with one simple rule (e.g. an angle, a multiplicant).
> It allows us to go from simple to complex and random with only one carefully picked out rule.
## 測驗 2
First we establish a **run** in a sequence of values to be *a subsequence as long as possible consisting entirely of the same value*. (Sometimes a run is defined to be of length at least two, but for the purpose of this explanation, we scrap that requirement.)
> 首先我們定義「連串(run, 中國翻遊程)」為一個序列之中,數值全部相同並且盡可能越長越好之子序列。(有時候一個「連串」的定義必須要是長度至少二的子序列,但這裡為方便解釋,我們忽略該條件限制。)
Consider the following sequence:
111116777344
The **runs** in this sequence would be 11111, 6, 777, 3 and 44.
:::warning
*Run* as a simple word in English has a myriad of meanings. In fact, according to the [NPR](https://www.npr.org/2011/05/30/136796448/has-run-run-amok-it-has-645-meanings-so-far), run has in total 645 meanings in The Oxford Dictionary. (See [here](https://www.oed.com/view/Entry/168872?rskey=mWVYst&result=2#eid) and [here](https://www.oed.com/view/Entry/168875?rskey=mWVYst&result=4#eid).)
In the field of Computer Science, it is no exception.
In the context of *sequence*, for example, **run** can also mean a *non-decreasing* subsequence of values as long as possible. When we consider the sequence 123234563345678234, the runs *by* this definition would be 123, 23456, 3345678 and 234.
A **run** can also mean an instance of the execution of a program or other task by a computer.
:::
Now let's examine the function:
```c
struct ListNode *deleteDuplicates(struct ListNode *head)
{
/* If head is NULL, return NULL */
if (!head)
return NULL;
if (COND1/*Is it a duplicate?*/) {
/* Remove all duplicate numbers */
while (COND2/*Are there more duplicates?*/)
/*If so, make head point to the next element*/
head = head->next;
/* When there is no more duplicate of the current number,\
* find the next non-duplicate element and return it. */
return deleteDuplicates(head->next);
}
/* If it is not a duplicate, make it point to the next non-duplicate.\
* Find the next non-duplicate by calling the function on the next \
* element. Afterwards, return itself.*/
head->next = deleteDuplicates(head->next);
return head;
}
```
The code here does one simple thing: take the head of a run and inspect it:
1. If the run has length > 2, return the first non-duplicate element after the run.
2. If the run has only one element (the element has no duplicates), make the element point to the next non-duplicate and return itself.
> 該函式做的事情一言以蔽之為:將一個連串的頭作為輸入並對其做檢驗:
> 1. 倘若該連串長度大於等於二,回傳其後第一個非重複的元素。
> 2. 倘若該連串長度為一(表示該元素不重複),則使其指向下一個不重複的元素,並回傳自己。
Consider the following intial configuration:
```mermaid
flowchart LR
n0((4))-->n1((6))-->n2((6))-->n3((6))-->n4((6))-->n5((9))-->n6((9))-->n7((13))-->...
head-->n0
style head fill:#fff, stroke-width:0px
style ... fill:#fff, stroke-width:0px
```
The program finds that 4 isn't a duplicate, so the following code is executed:
```c
head->next = deleteDuplicates(head->next);
```
This will make 4 point to the next non-duplicate.
But before that, the function is called on `head->next` to find the next non-duplicate.
In the following graph, there is a second `head`, which is the argument supplied to the second function call, in `deleteDuplicates(head->next)`:
```mermaid
flowchart LR
head-->n1
h0[head]-->n0
n0((4))--head->next-->n1((6))-->n2((6))-->n3((6))-->n4((6))-->n5((9))-->n6((9))-->n7((13))-->...
style head fill:#fff, stroke-width:0px
style h0 fill:#fff, stroke-width:0px
style ... fill:#fff, stroke-width:0px
```
The program then finds that 6 is a duplicate. So `head` points to the next element.
```c
head = head->next;
```
```mermaid
flowchart LR
head-->n2
h0[head]-->n0
style h0 fill:#fff, stroke-width:0px
n0((4))--head->next-->n1((6))-->n2((6))-->n3((6))-->n4((6))-->n5((9))-->n6((9))-->n7((13))-->NULL
style head fill:#fff, stroke-width:0px
style NULL fill:#fff, stroke-width:0px
```
In the while loop, the program finds that there are more 6 duplicates:
```mermaid
flowchart LR
head-->n3
h0[head]-->n0
style h0 fill:#fff, stroke-width:0px
n0((4))--head->next-->n1((6))-->n2((6))-->n3((6))-->n4((6))-->n5((9))-->n6((9))-->n7((13))-->NULL
style head fill:#fff, stroke-width:0px
style NULL fill:#fff, stroke-width:0px
```
Yet one more:
```mermaid
flowchart LR
h1((head))-->n4
h0[head]-->n0
style h0 fill:#fff, stroke-width:0px
n0((4))--head->next-->n1((6))-->n2((6))-->n3((6))-->n4((6))-->n5((9))-->n6((9))-->n7((13))-->NULL
style h1 fill:#fff, stroke-width:0px
style NULL fill:#fff, stroke-width:0px
```
The program finds that the next element isn't 6 anymore so it calls the function on the next element `head->next` to find the next non-duplicate.
```mermaid
flowchart LR
h1((head))-->n4
h2((head))-->n5
h0[head]-->n0
style h0 fill:#fff, stroke-width:0px
n0((4))--head->next-->n1((6))-->n2((6))-->n3((6))-->n4((6))--head->next-->n5((9))-->n6((9))-->n7((13))-->NULL
style h1 fill:#fff, stroke-width:0px
style h2 fill:#fff, stroke-width:0px
style NULL fill:#fff, stroke-width:0px
```
9 has a duplicate, head points to the next element:
```mermaid
flowchart LR
h1((head))-->n4
h2((head))-->n6
h0[head]-->n0
style h0 fill:#fff, stroke-width:0px
n0((4))--head->next-->n1((6))-->n2((6))-->n3((6))-->n4((6))--head->next-->n5((9))-->n6((9))-->n7((13))-->NULL
style h1 fill:#fff, stroke-width:0px
style h2 fill:#fff, stroke-width:0px
style NULL fill:#fff, stroke-width:0px
```
9 has no more duplicates. The function is called again:
```mermaid
flowchart LR
h1((head))-->n4
h2((head))-->n6
h3((head))-->n7
h0[head]-->n0
style h0 fill:#fff, stroke-width:0px
n0((4))--head->next-->n1((6))-->n2((6))-->n3((6))-->n4((6))--head->next-->n5((9))-->n6((9))--head->next-->n7((13))-->NULL
style h1 fill:#fff, stroke-width:0px
style h2 fill:#fff, stroke-width:0px
style h3 fill:#fff, stroke-width:0px
style NULL fill:#fff, stroke-width:0px
```
13 has no duplicates. Another function call:
```mermaid
flowchart LR
h1((head))-->n4
h2((head))-->n6
h3((head))-->n7
h4((head))-->NULL
h0[head]-->n0
style h0 fill:#fff, stroke-width:0px
n0((4))--head->next-->n1((6))-->n2((6))-->n3((6))-->n4((6))--head->next-->n5((9))-->n6((9))--head->next-->n7((13))--head->next-->NULL
style h1 fill:#fff, stroke-width:0px
style h2 fill:#fff, stroke-width:0px
style h3 fill:#fff, stroke-width:0px
style h4 fill:#fff, stroke-width:0px
style NULL fill:#fff, stroke-width:0px
```
```c
if (!head)
return NULL;
```
Since `head` now points to `NULL`, the current function returns `NULL`.
```mermaid
flowchart LR
h1((head))-->n4
h2((head))-->n6
h3((head))-->n7
h4((return))-->NULL
h0[head]-->n0
style h0 fill:#fff, stroke-width:0px
n0((4))--head->next-->n1((6))-->n2((6))-->n3((6))-->n4((6))--head->next-->n5((9))-->n6((9))--head->next-->n7((13))--head->next-->NULL
style h1 fill:#fff, stroke-width:0px
style h2 fill:#fff, stroke-width:0px
style h3 fill:#fff, stroke-width:0px
style h4 fill:#fff, stroke-width:0px
style NULL fill:#fff, stroke-width:0px
```
13 now points to the return value NULL, which happens to be the same as befor:
```c
head->next = deleteDuplicates(head->next);
```
```mermaid
flowchart LR
h1((head))-->n4
h2((head))-->n6
h3((head))-->n7
h0[head]-->n0
style h0 fill:#fff, stroke-width:0px
n0((4))--head->next-->n1((6))-->n2((6))-->n3((6))-->n4((6))--head->next-->n5((9))-->n6((9))--head->next-->n7((13))-->NULL
style h1 fill:#fff, stroke-width:0px
style h2 fill:#fff, stroke-width:0px
style h3 fill:#fff, stroke-width:0px
style NULL fill:#fff, stroke-width:0px
```
On the next line the `head` is returned.
```c
return (head);
```
```mermaid
flowchart LR
h1((head))-->n4
h2((head))-->n6
h3((return))---n7
h0[head]-->n0
style h0 fill:#fff, stroke-width:0px
n0((4))--head->next-->n1((6))-->n2((6))-->n3((6))-->n4((6))--head->next-->n5((9))-->n6((9))-->n7((13))-->NULL
style h1 fill:#fff, stroke-width:0px
style h2 fill:#fff, stroke-width:0px
style h3 fill:#fff, stroke-width:0px
style NULL fill:#fff, stroke-width:0px
```
The function that handles 9 returns the same element.
```mermaid
flowchart LR
h1((head))-->n4
h3((return))---n7
h0[head]-->n0
style h0 fill:#fff, stroke-width:0px
n0((4))--head->next-->n1((6))-->n2((6))-->n3((6))-->n4((6))-->n5((9))-->n6((9))-->n7((13))-->NULL
style h1 fill:#fff, stroke-width:0px
style h3 fill:#fff, stroke-width:0px
style NULL fill:#fff, stroke-width:0px
```
The fuction that handles 6 also returns the element 13:
```mermaid
flowchart LR
h3((return))---n7
h0[head]-->n0
style h0 fill:#fff, stroke-width:0px
n0((4))--head->next-->n1((6))-->n2((6))-->n3((6))-->n4((6))-->n5((9))-->n6((9))-->n7((13))-->NULL
style h3 fill:#fff, stroke-width:0px
style NULL fill:#fff, stroke-width:0px
```
The function for 4 takes the return value and points to it:
```c
head->next = deleteDuplicates(head->next);
```
```mermaid
flowchart LR
h0[head]-->n0
style h0 fill:#fff, stroke-width:0px
n0((4))-->n7
n1((6))-->n2((6))-->n3((6))-->n4((6))-->n5((9))-->n6((9))-->n7((13))-->NULL
style NULL fill:#fff, stroke-width:0px
```
This results in the removing of all nodes between `head`(4) and the return node(13):
```mermaid
flowchart LR
h0[head]-->n0
style h0 fill:#fff, stroke-width:0px
n0((4))-->n7((13))-->NULL
style NULL fill:#fff, stroke-width:0px
```
From the above demonstration, we know that to know if a head contains a duplicate value, we have to check:
1. If the next node isn't `NULL`. (e.g. The node with value 13 won't pass this.)
2. If the next node has the same value. (The node with value 4 won't pass this.)
So `COND1` should be:
```
!head->next && head->value != head->next->value
```
Note that `!head->next` should be the first condition to check because if `head->next == NULL`, the first condition fails and the next condition will not be checked, which avoids segmentation fault by accessing `head->next->value`.
Checking if there are more duplicates in a run requires basically the same conditions:
1. If the next node isn't `NULL`.
2. If the next node still has the same value.
So `COND2`, as with `COND1`, is also:
```
!head->next && head->value != head->next->value
```
## 測驗 2 延伸問題 Additional Problems
### Non-resursive (Iterative) Version
#### Thought Process
Following the program flow for the above code, we can see that the recursive functions are called from left to right and they return from right to left.
To make an iterative version, the flow has to go from left to right and end there.
##### First Try: Naive, Redundant
My mind first went into how many pointers to `struct List Node` I would have to maintain to achieve that, this was my conclusion:
1. One node `head` that keeps track of the new head.
* In cases where the first node is a duplicate, the head changes.
2. One node `tmp` that traverses the list from where `head` is and removes nodes according to the requirements.
* Stays one place before a run with duplicates and remove `tmp->next` until the next run is reached.
```c
struct ListNode *deleteDuplicates(struct ListNode *head)
{
/* Start traversing the list until the first non-duplicate\
* is found or until the end of the list */
while (head) {
/* nh now points to the first value of the run\
* If the next value is NULL or different, here is our\
* new first head */
if (!head->next || head->val != head->next->val) {
break;
} else {
/* If the next value is the same as that of the\
* current value, advance nh to find the first\
* occurence of the next different value or the\
* end */
/* nh->next != NULL && nh->val == nh->next->val */
do {
head = head->next;
} while (head->next && head->val == head->next->val);
/* The inner loop takes nh to the last value of\
* the run, so we need to advance it to either the\
* first value of the next run or NULL if it has\
* reached the end. */
head = head->next;
}
}
/* If head is NULL, return NULL */
if (!head)
return head;
struct ListNode *tmp = head;
while(tmp->next) {
/* If the next value is not the same as the next but\
* one value (the value after the next one), or if the\
* next node points to NULL, we have a single value.\
* We leave it alone and advance to the next node. */
if (!tmp->next->next || tmp->next->val != tmp->next->next->val) {
tmp = tmp->next;
} else {
/* If the next value is the same as the next but\
* one value, remove the next value until tmp->next\
* is a different value */
do {
tmp->next = tmp->next->next;
} while (tmp->next->next && tmp->next->val == tmp->next->next->val);
/* Remove the last node of the run so now tmp->next\
* is either the first value of the next run or NULL\
*/
tmp->next = tmp->next->next;
}
}
return head;
}
```
##### Second Try: Elegant, Still Not the Best
In the first try, `tmp` works by pointing to the last non-duplicate element and keeps removing the "next duplicate element". Since the head has no element before it, there is no way to delete the head the same way `tmp` does, which is why we handled them in different loops.
However, if I add a sentinel node `dummy` in front of the head and use a value `pred` (predecessor) the same way we use `tmp` in the first try, we can do it in one pass. Note that the return value would be `dummy->next`:
```c
struct ListNode *deleteDuplicates(struct ListNode *head)
{
struct ListNode *dummy = malloc(sizeof(struct ListNode));
dummy->next = head;
struct ListNode *pred = dummy;
while(pred->next) {
if (!pred->next->next || pred->next->val != pred->next->next->val) {
pred = pred->next;
} else {
do {
pred->next = pred->next->next;
} while (pred->next->next && pred->next->val == pred->next->next->val);
pred->next = pred->next->next;
}
}
return dummy->next;
}
```
##### Third Try: Tasteful
Keeping in mind what I have learned from [linked list 和非連續記憶體](https://hackmd.io/@sysprog/c-linked-list), I thought about using a pointer to pointer to allow deleting elements without accessing the previous element, which obviates the need to create a sentinel/dummy node.
```c
struct ListNode *deleteDuplicates(struct ListNode *head)
{
struct ListNode **tmp = &head;
while(*tmp) {
if (!(*tmp)->next || (*tmp)->val != (*tmp)->next->val)
tmp = &(*tmp)->next;
else {
/* dereferencing: changing struct members */
do *tmp = (*tmp)->next;
while ((*tmp)->next && (*tmp)->val == (*tmp)->next->val);
*tmp = (*tmp)->next;
}
}
return head;
}
```
### Rewrite the Code using a data structure similar to the Circular Doubly Linked-List used in Linux Kernel
First assume the following container structure:
```c
typedef struct {
int *val;
struct list_head list;
} element_t
```
... where `list_head` comes from the `list.h` library provided in the course.
#### Recursive
```c=
struct list_head *removeDuplicates(struct list_head *head, struct list_head *node)
{
/* Assume the function is called like this:\
* removeDuplicates(head, head->next);\
*/
if (node == head) /* End of the list */
return node;
if (node->next != head && list_entry(node, element_t, list)->val == list_entry(node->next, element_t, list)->val) {
/* Remove all duplicate numbers */
while (node->next != head && node->val == node->next->val)
node = node->next;
return removeDuplicates(node->next);
}
node->next = removeDuplicates(head->next);
node->next->prev = node;
return node;
}
```
Most of the code is the same, except:
1. end of list checking
2. In line 14 and 15, both `->next` and `->next->prev` needs to be updated.
:::warning
The original LeetCode problem seems to have confused *remove* and *delete*. Since this implementation doesn't deal with freeing memory, I changed the function name to `removeDuplicates`.
:::
#### Iterative: pointer to pointer
```c
struct list_head *removeDuplicates(struct list_head *head)
{
struct list_head **tmp = &head;
while(*tmp) {
if (!(*tmp)->next || list_entry((*tmp), element_t, list)->val != list_entry((*tmp)->next, element_t, list)->val)
tmp = &(*tmp)->next;
else {
//dereferencing: changing struct contents
do *tmp = (*tmp)->next;
while ((*tmp)->next && list_entry((*tmp), element_t, list)->val == list_entry((*tmp)->next, element_t, list)->val);
*tmp = (*tmp)->next;
(*tmp)->next->prev = *tmp;
}
}
return head;
}
```
#### Iterative: `prev`
```c
struct list_head *removeDuplicates(struct list_head *head)
{
struct list_head *tmp = head->next;
while(tmp) {
if (!tmp->next || list_entry((*tmp), element_t, list)->val != list_entry((*tmp)->next, element_t, list)->val)
tmp = tmp->next;
else {
do tmp = tmp->next;
while (tmp->next && list_entry((*tmp), element_t, list)->val == list_entry((*tmp)->next, element_t, list)->val);
tmp->prev->next = tmp->next;
tmp->next->prev = tmp->prev;
}
}
return head;
}
```
## 測驗 3
```
MMM1 = list_for_each_entry_safe
MMM2 = list_for_each_entry
MMM3 = list_for_each_entry
MMM4 = list_last_entry???
```
### 1. Code Walk-through
#### LRUCache
LRU stores the head to every node in the cache.
* `capacity`: The size of this cache.
* `count`: Current number of `LRUNodes` in the cache.
* `dhead`: Embedded list node that allows you to traverse all the nodes in the cache. The order also relates to how long it has been since the node's been accessed. The further to the right, the longer it has been.
* `hheads[]`: Hash table that allows for quick $~O(n)$ access.
```c
typedef struct {
int capacity, count;
struct list_head dhead, hheads[];
} LRUCache;
```
#### lRUNode
```c
typedef struct {
int key, value;
struct list_head hlink, dlink;
} LRUNode;
```
#### lRUCacheCreate
Create a cache of size `capacity`.
```c
LRUCache *lRUCacheCreate(int capacity)
{
/* Allocate memory for obj and all the cache nodes */
LRUCache *obj = malloc(sizeof(*obj) + capacity * sizeof(struct list_head));
obj->count = 0;
obj->capacity = capacity;
INIT_LIST_HEAD(&obj->dhead);
for (int i = 0; i < capacity; i++)
INIT_LIST_HEAD(&obj->hheads[i]);
return obj;
}
```
#### lRUCacheFree
Free the whole cache including all its nodes.
Since it needs to traverse `&obj->dhead`, `MMM1 = list_for_each_entry_safe`.
Why "safe"?
1. Only the safe version has four arguments.
2. Because we modify the nodes.
```c
void lRUCacheFree(LRUCache *obj)
{
LRUNode *lru, *n; /* n stores the next node in the traversal */
/* Traverse the list of cache nodes and release all of them */
MMM1 (lru, n, &obj->dhead, dlink) {
list_del(&lru->dlink);
free(lru);
}
free(obj);
}
```
#### lRUCacheGet
Find the cache in the hash table.
Since we need to traverse the hash bucket, `MMM2 = list_for_each_entry`
```c
int lRUCacheGet(LRUCache *obj, int key)
{
LRUNode *lru;
int hash = key % obj->capacity;
MMM2 (lru, &obj->hheads[hash], hlink) {
if (lru->key == key) {
list_move(&lru->dlink, &obj->dhead);
return lru->value;
}
}
return -1;
}
```
#### lRUCachePut
Add a new cache node.
Since `MMM3` is where we search for the key in the bucket, `MMM3 = list_for_each_entry`
`MMM4` is where we are evicting the last node in `dhead`, so `MMM4 = list_last_entry`
```c
void lRUCachePut(LRUCache *obj, int key, int value)
{
/* Add it in the hash table and dhead */
LRUNode *lru;
int hash = key % obj->capacity;
MMM3 (lru, &obj->hheads[hash], hlink) {
if (lru->key == key) {
/* If the same node is found in the list, move it to the head of dhead */
list_move(&lru->dlink, &obj->dhead);
lru->value = value;
/* Since no new node is added, no need to go on and do eviction */
return;
}
}
/* If the cache is at capacity, find the victim at the end of dhead,
* which is the least recently used node.
* If not, at the new node to the head of dhead and its corresponding
* hash bucket */
if (obj->count == obj->capacity) {
lru = MMM4(&obj->dhead, LRUNode, dlink);
list_del(&lru->dlink);
list_del(&lru->hlink);
} else {
lru = malloc(sizeof(LRUNode));
obj->count++;
}
lru->key = key;
list_add(&lru->dlink, &obj->dhead);
list_add(&lru->hlink, &obj->hheads[hash]);
lru->value = value;
}
```
:::warning
TODO:
I haven't figured out a way to write a test file to generate test data for this problem.
I did find this [paper](https://www.researchgate.net/publication/301371312_Test_Data_Generation_for_LRU_Cache-Memory_Testing) that can potentially point me in the right direction.
:::
### 2. LRU in Linux
## 測驗 4
### 1-1. Code Walk-through: Data Structures
#### seq_node
A node in the list, containing a number and a `list_head` node. Implements [**Instrusive Linked List**](https://www.data-structures-in-practice.com/intrusive-linked-lists/).
```c
struct seq_node {
int num;
struct list_head link;
};
```
#### find()
```c
static struct seq_node *find(int num, int size, struct list_head *heads)
{
struct seq_node *node;
/* modular hashing */
int hash = num < 0 ? -num % size : num % size;
/* find in bucket */
list_for_each_entry (node, &heads[hash], link) {
if (node->num == num)
return node;
}
/* did not find */
return NULL;
}
```
### 1.1 Code Walk-through: Implementation
#### `int longestConsecutive(int *nums, int n_size)`
##### Initialization
```c
/* hash table and its length */
int hash, length = 0;
struct seq_node *node; /* used to store the node currently acessing */
/* allocate space for the hash table */
struct list_head *heads = malloc(n_size * sizeof(*heads));
/* initialize buckets */
for (int i = 0; i < n_size; i++)
INIT_LIST_HEAD(&heads[i]);
```
##### Store Data
Traverse the list and put all numbers into the hash table. If a number appears more than twice, only one node is added of it.
```c
for (int i = 0; i < n_size; i++) {
/* If num doesn't already exists, create a seq_node with num in it and store it in hash table instrusively */
if (!find(nums[i], n_size, heads)) {
hash = nums[i] < 0 ? -nums[i] % n_size : nums[i] % n_size;
node = malloc(sizeof(*node));
node->num = nums[i];
list_add(&node->link, &heads[hash]);
}
}
```
:::success
Since any number appears only once in this hash table, we could refer to it as a **hash set**.
:::
##### Find Consecutive Sequences
Traverse the list and go from each new, unvisited number upwards and downwards to get the count of consecutive numbers.
```c=
for (int i = 0; i < n_size; i++) {
int len = 0;
int num;
/* First, search for the number in the hash table */
node = find(nums[i], n_size, heads);
/* If num exists in hash table, find consecutive sequence starting\
* from num bilaterally.
* TODO: Why do we need a while here? */
while (node) {
len++; /* Starting point itself adds 1 to the length */
num = node->num;
/* Delete visited num from hash table to avoid redundant calculation */
list_del(&node->link);
/* Two left will go from num leftwards and right vice versa */
int left = num, right = num;
/* If find next int down, add 1 to length */
while ((node = find(LLL, n_size, heads))) {
len++;
/* Delete visited num to avoid extraneous calculation */
list_del(&node->link);
}
/* When not find next int down, lower end of sequence cuts off and loop ends */
/* If find next int up, add 1 to length */
while ((node = find(RRR, n_size, heads))) {
len++;
/* Delete visited num to avoid unnecessary calculation */
list_del(&node->link);
}
/* When not find next int down, upper end of sequence cuts off and loop ends */
/* Update max length */
length = len > length ? len : length;
}
}
return length;
```
From the logic delineated in the comments above:
1. In line 23, since the program ought to search for the **next** integer down (the number 1 smaller than the current), the answer for LLL should be the pre-decremented `--left`.
* Decremented because its searching for the next "smaller" number.
* Prefixed to avoid accouting for the starting number again.
2. In line 31, since the program ought to search for the **next** integer up (the number 1 greater than the current), the answer for RRR should be the pre-incremented `++right`.
* Incremented because its searching for the next "greater" number.
* Prefixed to avoid accouting for the starting number again.
### 1.2 Testing
I wrote a python program to test the code.
[Test code here on Google Colab (comments are welcome!)](https://colab.research.google.com/drive/1sz3ik0MJaBaxeUcC9ehfCRPr0sCyMSwW#scrollTo=f1JVwfIhvo8i)
Here's a snippet of the code where I generate test data:
```python=
def generateTestData(max_num=max_num, max_array_size=max_array_size, debug=False, set_answer=0):
answer = randint(1, max_array_size)
if debug:
answer = set_answer
start_num = randrange(0, max_num - answer)
num_pool = list(range(start_num, start_num + answer)) #range doesn't create a list
array_size = randint(answer, max_array_size)
list_of_sequences = []
my_list = [0]*array_size
consecutive_invalid_count = 0
max_consecutive_invalid_count = 0
n_upper_bound = max_num
n_lower_bound = 0
for it in range(0, array_size):
if (len(num_pool) > 0 and randint(0, 1) == 0) or array_size-it <= len(num_pool):
i = randrange(0, len(num_pool))
my_list[it] = num_pool[i]
num_pool.pop(i)
else:
while True:
n = randrange(n_lower_bound, n_upper_bound)
if start_num + answer > n >= start_num:
my_list[it] = n
break
if n == start_num-1 or n == start_num + answer:
continue
n_valid = True
n_added_to_ranges = False
for i in range(0, len(list_of_sequences)):
if list_of_sequences[i][0] == n + 1: #add to back, check len first
if list_of_sequences[i][1] - list_of_sequences[i][0] + 1 >= answer:
n_valid = False
break
list_of_sequences[i][0] = n
n_added_to_ranges = True
break
elif list_of_sequences[i][1] == n - 1: #add to front, check len first
if list_of_sequences[i][1] - list_of_sequences[i][0] + 1 >= answer:
n_valid = False
break
list_of_sequences[i][1] = n
n_added_to_ranges = True
if i+1 < len(list_of_sequences) and list_of_sequences[i+1][0] == n+1: #fill gap, merge (check len first)
if list_of_sequences[i+1][1] - list_of_sequences[i][0] + 1 > answer:
n_valid = False
break
list_of_sequences[i][1] = list_of_sequences[i+1][1]
list_of_sequences.pop(i+1)
break
elif n < list_of_sequences[i][0] - 1: #n in the gap, not touching any ranges
list_of_sequences.insert(i, [n, n]) #(index, item)
n_added_to_ranges = True
break
elif list_of_sequences[i][1] >= n >= list_of_sequences[i][0]: #n already inside a range
n_added_to_ranges = True
break
if n_valid and not n_added_to_ranges:
list_of_sequences.append([n, n])
if n_valid:
my_list[it] = n
consecutive_invalid_count = 0
break
else:
consecutive_invalid_count += 1
max_consecutive_invalid_count = max(max_consecutive_invalid_count, consecutive_invalid_count)
if (consecutive_invalid_count >= 10):
n_upper_bound = start_num + answer
n_lower_bound = start_num
print("consecutive_invalid_count >= 10")
if debug:
print(list_of_sequences)
print(max_consecutive_invalid_count)
return answer, array_size, my_list, start_num, num_pool
```
#### Test Data Generation Rules
* `answer` is a random number that will be the size of the longest consecutive sequence.
* `start_num` is the starting number of that sequence.
* If `answer = 5` and `start_num = 3`, 3, 4, 5, 6, and 7 will be in the array and 2 and 8 can't be in the list.
* `array_size` is the size of the array. It should be greater than the answer.
* After initializing all the parameters, I start filling in the numbers, but there's one more thing to be aware of:
* In addition to making sure there is a seqence that starts with `start_num` of size `answer`, I also need to make sure other sequences don't have sizes longer than `answer` (which will change the answer).
So I maintain a list `list_of_sequences` to keep track of all the consecutive sequences.
* If we reach a point where all the other sequences are either already of size `answer` or that the gaps are all of size 1 and filling any of them would result in a combined size bigger than `answer`, I will just make sure the rest of the numbers are in between `start_num` and `start_num + answer`, so that the answer doesn't change.
<!--:::warning
TODO: There should be a way to fix that before abandoning it, e.g. adding one number to the last sequence if the biggest number is 1 lower than `max_num`, etc. I might leave that endeavor for later.
:::-->
### 1.3 Improvement - While Loop
In line 11, after calling `find()` on `num`, there is a while loop that executes if the return value `node` isn't `NULL` (i.e. `num` is found). However, I didn't think the loop would be executed more than once:
* If we look in the while loop, there are two "inner" while loops. `node` is last modified in the second inner while loop:
```c
while ((node = find(++right, n_size, heads)))
```
* Whenver execution leaves this while loop, that means `node == NULL`, and the condition for the outer while loop is `node`, which means the next iteration of the outer while loop can never happen. Which means the second while loop is effectively the same as a simple `if` statement.
* I've tested it with my python program by making the while loop print something in the second iteration and nothing was printed out of more than 1,000 tests.
* Moreover, when I changed `while` to `if`, the tests ran fine, no errors occurred from it.
### 1.3 Improvement - Time: Exit the Loop Early
The complexity of the original code is $O(n)$:
* There are three loops, each running $n$ iterations.
* Although there are two inner loops in the third loop, it's easy to see that the two inner loops in aggregate only runs at most $O(n)$ iterations (instead of $O(n^2)$, which we'd usually expect of most second-level loops) during the entire function execution because `list_delete(&node->link)` can only be called on each element **once**.
Since there is no escaping having to look at every node at least once, $O(n)$ is the best time complexity we can get, but we can still do some fine-tuning to make the execution slightly faster:
* The third loop doesn't have to run exactly `n_size` iterations. When the number of nodes not visited in the third loop is smaller than `length` (the greatest length so far), it's impossible to do better with the little number of nodes left. At that point, we can break away from the loop early:
```c
for (int i = 0; i < n_size - length; i++) { /* this line is modified */
int len = 0;
int num;
node = find(nums[i], n_size, heads);
while (node) {
len++;
num = node->num;
list_del(&node->link);
int left = num, right = num;
while ((node = find(--left, n_size, heads))) {
len++;
list_del(&node->link);
}
while ((node = find(++right, n_size, heads))) {
len++;
list_del(&node->link);
}
length = len > length ? len : length;
}
}
return length;
```
### 1.4 Improvement - Handling Memory Leak
* Since this code implements intrusive linked lists, the **container** of the list nodes need to be released too after the node is deleted.
* The memory used for list heads are allocated in this line: `struct list_head *heads = malloc(n_size * sizeof(*heads))`. That memory needs to be freed too.
```c
int longestConsecutive(int *nums, int n_size)
{
int hash, length = 0;
struct seq_node *node;
struct list_head *heads = malloc(n_size * sizeof(*heads));
for (int i = 0; i < n_size; i++)
INIT_LIST_HEAD(&heads[i]);
for (int i = 0; i < n_size; i++) {
if (!find(nums[i], n_size, heads)) {
hash = nums[i] < 0 ? -nums[i] % n_size : nums[i] % n_size;
node = malloc(sizeof(*node));
node->num = nums[i];
list_add(&node->link, &heads[hash]);
}
}
for (int i = 0; i < n_size - length; i++) {
int len = 0;
int num;
node = find(nums[i], n_size, heads);
while (node) {
len++;
num = node->num;
list_del(&node->link);
free(node); /* Improvement */
int left = num, right = num;
while ((node = find(--left, n_size, heads))) {
len++;
list_del(&node->link);
free(node); /* Improvement */
}
while ((node = find(RRR, n_size, heads))) {
len++;
list_del(&node->link);
free(node); /* Improvement */
}
length = len > length ? len : length;
}
}
free(heads); /* Improvement */
return length;
}
```
### 2. Linux Style Hash Table
Here I recycle some of the code from problem one and try applying my learning from that problem.
#### Data Structures
```c
struct hlist_node { struct hlist_node *next, **pprev; };
struct hlist_head { struct hlist_node *first; };
typedef struct { int bits; struct hlist_head *ht; } map_t;
/* It's a hash set, so only key is needed, data is not. */
struct hash_key {
int key;
struct hlist_node link;
};
```
#### Utility Functions
Most of the functions I need can be found in the first problem, except a node deletion function.
So I first look at how Linux implements a hash node delettion:
```c
static inline void __hlist_del(struct hlist_node *n)
{
struct hlist_node *next = n->next;
struct hlist_node **pprev = n->pprev;
WRITE_ONCE(*pprev, next);
if (next)
WRITE_ONCE(next->pprev, pprev);
}
```
`WRITE_ONCE` is defined in `linux/compiler.h`:
```c
#define WRITE_ONCE(var, val) \
(*((volatile typeof(val) *)(&(var))) = (val))
```
So `WRITE_ONCE(*pprev, next)` is effectively `*prev = next`.
See [this post](https://stackoverflow.com/questions/34988277/write-once-in-linux-kernel-lists) to see why it is used.
This is my version of it:
```c
static void map_del(struct hlist_node *n)
{
struct hlist_node *next = n->next;
struct hlist_node **pprev = n->pprev;
*pprev = next;
if (next)
next->pprev = pprev;
free(n);
}
```
I also modified the add function:
```c
static struct hash_key *find_key(map_t *map, int key) {
struct hlist_head *head = &(map->ht)[hash(key, map->bits)];
for (struct hlist_node *p = head->first; p; p = p->next) {
struct hash_key *kn = container_of(p, struct hash_key, link); /* link instead of node */
if (kn->key == key)
return kn;
}
return NULL;
}
void map_add(map_t *map, int key)
{
struct hash_key *kn = find_key(map, key);
if (kn)
return;
kn = malloc(sizeof(struct hash_key));
kn->key = key; /* no data */
struct hlist_head *h = &map->ht[hash(key, map->bits)];
struct hlist_node *n = &kn->l, *first = h->first;
n->next = first;
if (first)
first->pprev = &n->next;
h->first = n;
n->pprev = &h->first;
}
void map_deinit(map_t *map)
{
if (!map)
return;
for (int i = 0; i < MAP_HASH_SIZE(map->bits); i++) {
struct hlist_head *head = &map->ht[i];
for (struct hlist_node *p = head->first; p;) {
struct hash_key *kn = container_of(p, struct hash_key, link); /* link instead of node*/
struct hlist_node *n = p;
p = p->next;
if (!n->pprev) /* unhashed */
goto bail;
struct hlist_node *next = n->next, **pprev = n->pprev;
*pprev = next;
if (next)
next->pprev = pprev;
n->next = NULL, n->pprev = NULL;
bail:
free(kn); /* no data */
}
}
free(map);
}
```
##### `longestConsecutiveSequence()`
```c
int longestConsecutive(int *nums, int n_size)
{
map_t *map;
for(int i = 1; i <= 32; ++i) {
if (n_size >> i == 0) {
map = map_init(i);
break;
}
}
int length = 0;
struct hash_key *node;
for (int i = 0; i < n_size; i++) {
if (!find_key(map, nums[i])){
map_add(map,nums[i]);
}
}
for (int i = 0; i < n_size - length; i++) {
int len = 0;
int num;
node = find_key(map, nums[i]);
while (node) {
len++;
num = node->key;
map_del(&node->link);
free(node);
int left = num, right = num;
while ((node = find_key(map, --left))) {
len++;
map_del(&node->link);
free(node);
}
while ((node = find_key(map, ++right))) {
len++;
map_del(&node->link);
free(node);
}
length = len > length ? len : length;
}
}
map_deinit(map);
return length;
}
```
The above code is also put in this [python notebook](https://colab.research.google.com/drive/1sz3ik0MJaBaxeUcC9ehfCRPr0sCyMSwW#scrollTo=OwMvGzrGvzz-) for testing.
## Resources & References
[Edotor: Online Graphviz Editor](https://edotor.net/)
[Graphviz Brief Intro](https://www.worthe-it.co.za/blog/2017-09-19-quick-introduction-to-graphviz.html)
[Hashing Washington University in St. Louis](https://classes.engineering.wustl.edu/cse241/handouts/hash-functions.pdf)
[Hashing Cornell](https://www.cs.cornell.edu/courses/cs3110/2008fa/lectures/lec21.html#:~:text=Multiplicative%20hashing%20sets%20the%20hash,a%2C%20m%2C%20and%20q.)
[B.R. Preiss](https://web.archive.org/web/20161121124236/http://brpreiss.com/books/opus4/html/page214.html)
[EXploring Knuth's Multiplicative Hash](https://lowrey.me/exploring-knuths-multiplicative-hash-2/)
[Render math formula & graphs](https://hackmd.io/MathJax-and-UML?both)
[Spirals](https://www.geogebra.org/m/fh7jp5mq)
[Fibonacci Numbers and Nature](https://r-knott.surrey.ac.uk/Fibonacci/fibnat.html)
[The Golden Ratio (why it is so irrational) - Numberphile](https://www.youtube.com/watch?v=sj8Sg8qnjOg)
[Fibonacci Hashing: The Optimization that the World Forgot (or: a Better Alternative to Integer Modulo)](https://probablydance.com/2018/06/16/fibonacci-hashing-the-optimization-that-the-world-forgot-or-a-better-alternative-to-integer-modulo/)
[Syntax CodiMD](https://hackmd.io/@codimd/extra-supported-syntax#Youtube)
[Generice Hashing Functions and The Platform Problem](https://lwn.net/Articles/687494/)