834.Sum of Distances in Tree
===

###### tags: `Hard`,`DFS`,`DP`,`Tree`,`Graph`

[834. Sum of Distances in Tree](https://leetcode.com/problems/sum-of-distances-in-tree/)

### 題目描述

There is an undirected connected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges.

You are given the integer `n` and the array `edges` where `edges[i]` = [$a_i$, $b_i$] indicates that there is an edge between nodes $a_i$ and $b_i$ in the tree.

Return an array `answer` of length `n` where `answer[i]` is the sum of the distances between the i^th^ node in the tree and all other nodes.

### 範例

**Example 1:**


Input: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
Output: [8,12,6,10,10,10]
Explanation: The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer[0] = 8, and so on.

**Example 2:**


Input: n = 1, edges = []
Output: [0]

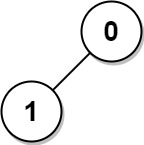
**Example 3:**


Input: n = 2, edges = [[1,0]]
Output: [1,1]

**Constraints**:

* 1 <= `n` <= 3 * 10^4^
* `edges.length` == `n` - 1
* `edges[i].length` == 2
* 0 <= $a_i$, $b_i$ < `n`
* $a_i$ != $b_i$
* The given input represents a valid tree.

### 解答
#### Python

class Solution:
    def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:
        from collections import defaultdict
        dict_node2edge = defaultdict(list)
        self.dict_visit = defaultdict(list)
        for e in edges:
            dict_node2edge[e[0]].append(e[1])
            dict_node2edge[e[1]].append(e[0])
            self.dict_visit[ (e[0],e[1]) ] = 0
            self.dict_visit[ (e[1],e[0]) ] = 0
            
        def dfs(node):
            currentnode_subtree_distance = 0
            node_cnt = 1
            father = node
            #print('current node', node)
            for child in dict_node2edge[father]:
                if self.dict_visit[ (father,child) ] or self.dict_visit[ (child,father) ]:
                    continue
                
                self.dict_visit[ (father,child) ] = 1
                self.dict_visit[ (child,father) ] = 1
                dist, nc = dfs( child )

                currentnode_subtree_distance += dist
                node_cnt += nc
                self.node_parentnode[child] = father
                self.childs[father].append(child)

            self.subtree_distance[node] = (currentnode_subtree_distance , node_cnt)
            #print('dfs', node, currentnode_subtree_distance, node_cnt)
            return currentnode_subtree_distance + node_cnt, node_cnt


        #Set 0 node as root
        #layer by layer calculate sub tree layer
        self.subtree_distance = dict() #know each node's subtree stat
        self.childs = dict() #know where to find node's edge
        for i in range(n):
            self.childs[i] = []
        self.node_parentnode = dict() #know who is your parent
        self.edge_visit = [0] * len(edges)

        ans = dict()
        a, b = dfs(0)
        ans[0] = a - b

        nodes = [0]
        while len(nodes) != 0:
            node = nodes.pop()
            nodes = self.childs[node] + nodes
            if node == 0:
                continue
            else:
                #print(node, self.node_parentnode[node])
                #print(ans[ self.node_parentnode[node] ])
                #print(self.subtree_distance[node])
                ans[node] = ans[ self.node_parentnode[node] ] + n - 2*(self.subtree_distance[node][1])
            #print(node, ans[node])
        
        return [ans[node] for node in range(n)]

> [name=玉山][time=Thu, Dec 26, 2022]

class Solution:
    def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:
        res = [0] * n
        cnt = [1] * n
        graph = [[] for _ in range(n)]

        for a, b in edges:
            graph[a].append(b)
            graph[b].append(a)
        
        def dfs1(node = 0, parent = -1):
            for child in graph[node]:
                if child == parent: continue
                dfs1(child, node)
                cnt[node] += cnt[child]
                res[node] += res[child] + cnt[child]
        
        def dfs2(node = 0, parent = -1):
            for child in graph[node]:
                if child == parent: continue
                res[child] = res[node] - 2*cnt[child] + n
                dfs2(child, node)
        
        dfs1()
        dfs2()

        return res

> [name=Yen-Chi Chen][time=Thu, Dec 22, 2022]
#### C++

class Solution {
public:
    vector<vector<int>> tree;
    vector<int> res, count;

    void dfs1(int root, int parent = -1) {
        for (int child : tree[root]) {
            if (child == parent) continue;
            dfs1(child, root);
            count[root] += count[child];
            res[root] += res[child] + count[child];
        }
    }

    void dfs2(int root, int parent = -1) {
        for (int child : tree[root]) {
            if (child == parent) continue;
            res[child] = res[root] - 2*count[child] + count.size();
            dfs2(child, root);
        }
    }

    vector<int> sumOfDistancesInTree(int n, vector<vector<int>>& edges) {
        tree.resize(n);
        res.assign(n, 0);
        count.assign(n, 1);

        for (const auto& edge : edges) {
            tree[edge[0]].push_back(edge[1]);
            tree[edge[1]].push_back(edge[0]);
        }
        dfs1(0);
        dfs2(0);
        return res;
    }
};

> [name=Yen-Chi Chen][time=Thu, Dec 22, 2022]

#### Javascript

一樣TLE我好爛

function sumOfDistancesInTree(n, edges) {
  const graph = [];
  for (const [v1, v2] of edges) {
    graph[v1] = graph[v1] ?? [];
    graph[v2] = graph[v2] ?? [];
    graph[v1].push(v2);
    graph[v2].push(v1);
  }

  const distances = new Array(n).fill(0);
  for (let i = 0; i < n; i++) {
    const visited = new Array(n).fill(false);
    const stack = [[i, 0]];

    // 做DFS 依序累加距離
    while (stack.length) {
      const [node, step] = stack.pop();
      if (visited[node]) continue;

      visited[node] = true;
      if (graph[node] === undefined) continue; // 沒有相鄰的點

      for (const vertex of graph[node]) {
        if (visited[vertex]) continue;
        distances[i] += step + 1;
        stack.push([vertex, step + 1]);
      }
    }
  }

  return distances;
}

> [name=Marsgoat][time=Thu, Dec 22, 2022]

function sumOfDistancesInTree2(n, edges) {
  const graph = new Array(n).fill(0).map(() => []);
  for (const [v1, v2] of edges) {
    graph[v1].push(v2);
    graph[v2].push(v1);
  }

  const distances = new Array(n).fill(0);
  const counts = new Array(n).fill(1);

  function dfs(node, parent) {
    for (const vertex of graph[node]) {
      if (vertex === parent) continue;
      dfs(vertex, node);
      counts[node] += counts[vertex];
      distances[node] += distances[vertex] + counts[vertex];
    }
  }

  function dfs2(node, parent) {
    for (const vertex of graph[node]) {
      if (vertex === parent) continue;
      distances[vertex] = distances[node] - counts[vertex] + n - counts[vertex];
      dfs2(vertex, node);
    }
  }

  dfs(0, -1);
  dfs2(0, -1);

  return distances;
}

> 感謝吉神教學，終於看懂了
> [name=Marsgoat][time=Jan 5, 2023]

### Reference

吉神教學

> 吉神：
> 經過第一次DFS之後我們有跟節點到所有點的距離總和了
> 此時如果想要再一次DFS就完工的話，就要去想，從某一個點下來時，結果會怎麼改變？
> 從圖上來看，當我們從原先的a點走到b點時，跟a點所在的藍色區域中所有的點的距離都多了1，跟綠色區域中所有的點的距離都少了1
> 藍色區域的數量又等於`n - 綠色區域的數量`
> 所以我們就有`ans[b]` = `ans[a]` + `n` - 2*`count[a]`
> 把算法列出來，這題就簡單了

[回到題目列表](https://hackmd.io/@Marsgoat/leetcode_every_day)