790.Domino and Tromino Tiling
===

###### tags: `Medium`,`DP`

[790. Domino and Tromino Tiling](https://leetcode.com/problems/domino-and-tromino-tiling/)

### 題目描述

You have two types of tiles: a `2 x 1` domino shape and a tromino shape. You may rotate these shapes.


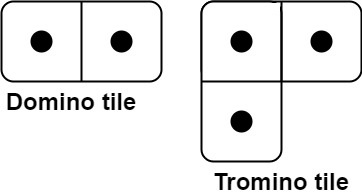
Given an integer n, return *the number of ways to tile an* `2 x n` *board*. Since the answer may be very large, return it **modulo** 10^9^ + 7.

In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.

### 範例

**Example 1:**


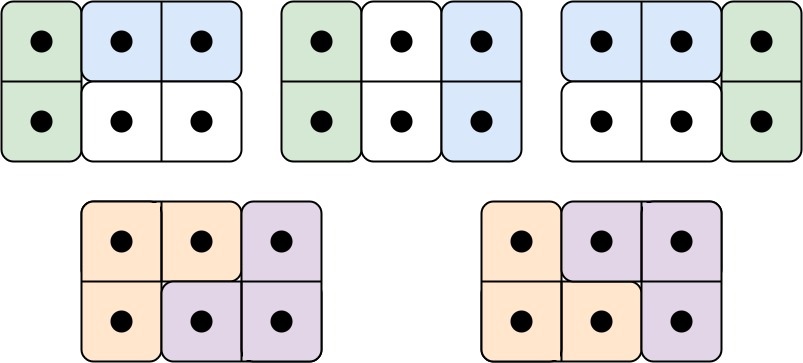
Input: n = 3
Output: 5
Explanation: The five different ways are show above.

**Example 2:**

Input: n = 1
Output: 1

**Constraints**:

* 1 <= `n` <= 1000

### 解答

#### C++

class Solution {
public:
    int numTilings(int n) {
        long long p1 = 1, p2 = 0, p3 = -1, ans;
        for (int i = 0; i < n; i++) {
            ans = (p1 * 2 + p3) % 1000000007;
            p3 = p2;
            p2 = p1;
            p1 = ans;
        }
        return ans;
    }
};

> [name=Yen-Chi Chen][time=Sat, Dec 24, 2022]

#### Python

class Solution:
    def numTilings(self, n: int) -> int:
        p1, p2, p3 = 1, 0, -1
        for _ in range(n):
            p1, p2, p3 = (p1 * 2 + p3) % 1000000007, p1, p2
        return p1

> [name=Yen-Chi Chen][time=Sat, Dec 24, 2022]

class Solution:

    def numTilings(self, n: int) -> int:
        flat = [0,1,2,5]
        unflat = [0,0,1,2]
        if n < 4:
            return flat[n]

        for i in range(4,n+1):
            #update flat
            flat.append( (flat[i-1]+2*unflat[i-1]+flat[i-2])%1000000007)
            #update unflat
            unflat.append( (flat[i-2]+unflat[i-1])%1000000007)

        #print(flat, unflat)
        return flat[-1]

> 
> [name=玉山][time=Mon, Dec 26, 2022]

### Reference

[回到題目列表](https://hackmd.io/@Marsgoat/leetcode_every_day)