787.Cheapest Flights Within K Stops
===

###### tags: `Medium`,`DP`,`DFS`,`BFS`,`Graph`,`Heap`

[787. Cheapest Flights Within K Stops](https://leetcode.com/problems/cheapest-flights-within-k-stops/)

### 題目描述
There are `n` cities connected by some number of flights. You are given an array `flights` where `flights[i]` = [$from_i$, $to_i$, $price_i$] indicates that there is a flight from city $from_i$ to city $to_i$ with cost $price_i$.

You are also given three integers `src`, `dst`, and `k`, return ***the cheapest price** from* `src` *to* `dst` *with at most* `k` *stops*. If there is no such route, return `-1`.

### 範例

**Example 1:**


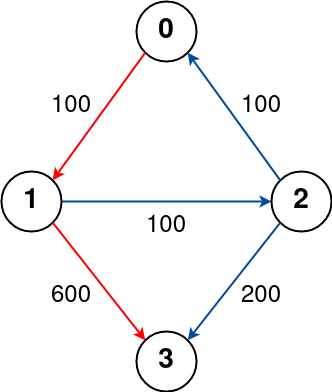
Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1
Output: 700
Explanation:
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700.
Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.

**Example 2:**


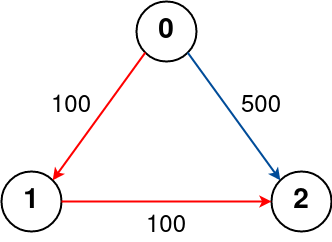
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
Output: 200
Explanation:
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.

**Example 3:**


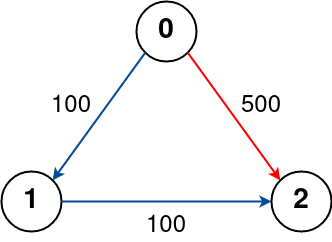
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0
Output: 500
Explanation:
The graph is shown above.
The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.

**Constraints**:

* 1 <= n <= 100
* 0 <= `flights.length` <= `(n * (n - 1) / 2)`
* `flights[i].length` == 3
* 0 <= $from_i$, $to_i$ < `n`
* $from_i$ != $to_i$
* 1 <= $price_i$ <= 10^4^
* There will not be any multiple flights between two cities.
* 0 <= `src`, `dst`, `k` < `n`
* `src` != `dst`

### 解答
#### C++

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        vector<vector<pair<int, int>>> graph(n);
        for (auto f : flights) {
            graph[f[0]].push_back({f[1], f[2]});
        }
        vector<int> prices(n, INT_MAX);
        queue<pair<int, int>> q;
        int depth = k + 1;
        q.push({src, 0});
        while (!q.empty()) {
            if (depth == 0) break;
            int num = q.size();
            for (int i = 0; i < num; i++) {
                auto cur = q.front(); q.pop();
                for (auto e : graph[cur.first]) {
                    int price = cur.second + e.second;
                    if (price < prices[e.first]) {
                        prices[e.first] = price;
                        q.push({e.first, price});
                    }
                }
            }
            depth--;
        }
        if (prices[dst] == INT_MAX) return -1;
        return prices[dst];
    }
};

> [name=Yen-Chi Chen][time=Thu, Jan 26, 2023]

#### Python

class Solution:
    def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
        
        dist_list = [[] for _ in range(n)]
        for city, cityTo, price in flights:
            dist_list[city].append((cityTo, price))
            
        que = [(src, 0)]
        minTotal = [float('INF')] * n

        while (que and k>=0):
            for _ in range(len(que)):
                curCity, curPrice = que.pop(0)
                for neibor, price in dist_list[curCity]:
                    if curPrice + price < minTotal[neibor]:
                        minTotal[neibor] = curPrice + price
                        que.append((neibor, minTotal[neibor]))
            k-=1
        
        return minTotal[dst] if minTotal[dst]!=float('INF') else -1

> [name=Dan][time=Tomorrow is Monday, happy working, Jan 29, 2023]

### Reference

[回到題目列表](https://hackmd.io/@Marsgoat/leetcode_every_day)