2492.Minimum Score of a Path Between Two Cities
===

###### tags: `Medium`,`DFS`,`BFS`,`Graph`

[2492. Minimum Score of a Path Between Two Cities](https://leetcode.com/problems/minimum-score-of-a-path-between-two-cities/)

### 題目描述

You are given a positive integer `n` representing `n` cities numbered from `1` to `n`. You are also given a 2D array `roads` where `roads[i]` = [$a_i$, $b_i$, $distance_i$] indicates that there is a **bidirectional** road between cities $a_i$ and $b_i$ with a distance equal to $distance_i$. The cities graph is not necessarily connected.

The **score** of a path between two cities is defined as the **minimum** distance of a road in this path.

Return *the **minimum** possible score of a path between cities* `1` *and* `n`.

**Note:**

* A path is a sequence of roads between two cities.
* It is allowed for a path to contain the same road **multiple** times, and you can visit cities `1` and `n` multiple times along the path.
* The test cases are generated such that there is **at least** one path between `1` and `n`.

### 範例

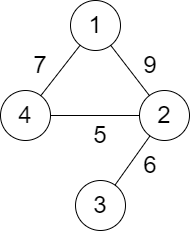
**Example 1:**


Input: n = 4, roads = [[1,2,9],[2,3,6],[2,4,5],[1,4,7]]
Output: 5
Explanation: The path from city 1 to 4 with the minimum score is: 1 -> 2 -> 4. The score of this path is min(9,5) = 5.
It can be shown that no other path has less score.

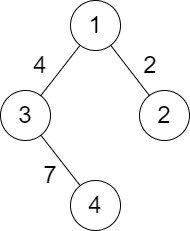
**Example 2:**


Input: n = 4, roads = [[1,2,2],[1,3,4],[3,4,7]]
Output: 2
Explanation: The path from city 1 to 4 with the minimum score is: 1 -> 2 -> 1 -> 3 -> 4. The score of this path is min(2,2,4,7) = 2.

**Constraints**:

* 2 <= `n` <= 10^5^
* 1 <= `roads.length` <= 10^5^
* `roads[i].length` == 3
* 1 <= $a_i$, $b_i$ <= `n`
* $a_i$ != $b_i$
* 1 <= $distance_i$ <= 10^4^
* There are no repeated edges.
* There is at least one path between `1` and `n`.

### 解答
#### C++

class Solution {
public:
    int minScore(int n, vector<vector<int>>& roads) {
        vector<vector<pair<int, int>>> graph(n + 1);
        for (auto road : roads) {
            graph[road[0]].push_back({road[1], road[2]});
            graph[road[1]].push_back({road[0], road[2]});
        }
        vector<bool> visit(n+1);
        queue<int> q;
        q.push(1);
        int ans = INT_MAX;
        while (!q.empty()) {
            auto node = q.front(); q.pop();
            for (auto [child, distance] : graph[node]) {
                ans = min(ans, distance);
                if (visit[child]) continue;
                visit[child] = true;
                q.push(child);
            }
        }
        return ans;
    }
};

> [name=Yen-Chi Chen][time=Wed, Mar 22, 2023]

#### Python

class Solution:
    def minScore(self, n: int, roads: List[List[int]]) -> int:
        self.ans = math.inf
        graph = defaultdict(list)

        for a, b, dis in roads:
            graph[a].append((b, dis))
            graph[b].append((a, dis))

        vis = set()

        def dfs(node):
            vis.add(node)

            for nei, cost in graph[node]:
                self.ans = min(self.ans, cost)
                if nei in vis:
                    continue
                dfs(nei)

        dfs(1)
        return self.ans

> [name=Ron Chen][time=Wed, Mar 22, 2023]

#### Javascript

function minScore(n, roads) {
  const graph = new Array(n + 1).fill(0).map(() => []);
  for (const [v1, v2, score] of roads) {
    graph[v1].push([v2, score]);
    graph[v2].push([v1, score]);
  }

  const visited = new Array(n + 1).fill(false);
  const stack = [[1, Infinity]];
  let minScore = Infinity;

  while (stack.length) {
    const [node, score] = stack.pop();
    minScore = Math.min(minScore, score);
    if (visited[node]) continue;
    visited[node] = true;
    for (const [vertex, vertexScore] of graph[node]) {
      stack.push([vertex, vertexScore]);
    }
  }

  return minScore;
}

> [name=Marsgoat][time=Wed, Mar 22, 2023]

### Reference

[回到題目列表](https://hackmd.io/@Marsgoat/leetcode_every_day)