2360.Longest Cycle in a Graph
===

###### tags: `Hard`,`DFS`,`Graph`

[2360. Longest Cycle in a Graph](https://leetcode.com/problems/longest-cycle-in-a-graph/)

### 題目描述

You are given a **directed** graph of `n` nodes numbered from `0` to `n - 1`, where each node has **at most one** outgoing edge.

The graph is represented with a given **0-indexed** array `edges` of size `n`, indicating that there is a directed edge from node `i` to node `edges[i]`. If there is no outgoing edge from node `i`, then `edges[i] == -1.`

Return *the length of the **longest** cycle in the graph. If no cycle exists, return* `-1`.

A cycle is a path that starts and ends at the **same** node.

### 範例

**Example 1:**


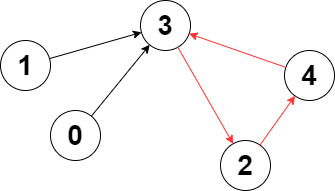
Input: edges = [3,3,4,2,3]
Output: 3
Explanation: The longest cycle in the graph is the cycle: 2 -> 4 -> 3 -> 2.
The length of this cycle is 3, so 3 is returned.

**Example 2:**


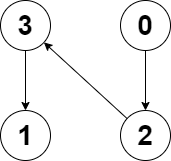
Input: edges = [2,-1,3,1]
Output: -1
Explanation: There are no cycles in this graph.

**Constraints**:

* `n` == `edges.length`
* 2 <= `n` <= 10^5^
* -1 <= `edges[i]` < n
* `edges[i]` != i

### 解答
#### C++

class Solution {
public:
    int longestCycle(vector<int>& edges) {
        int N = edges.size(), time = 1, ans = -1;
        vector<int> visit_time(N, 0);
        for(int i = 0; i < N; i++) {
            if (visit_time[i]) continue;
            int start = time, cur = i;
            while (cur != -1 && visit_time[cur] == 0) {
                visit_time[cur] = time++;
                cur = edges[cur];
            }
            if (cur != -1 && visit_time[cur] >= start) {
                ans = max(ans, time - visit_time[cur]);
            }
        }
        return ans;
    }
};

> [name=Yen-Chi Chen][time=Sun, Mar 26, 2023]

#### Python

class Solution:
    def longestCycle(self, edges: List[int]) -> int:
        N = len(edges)
        visit_time = [0] * N
        time = 1
        ans = -1
        for node in range(N):
            if visit_time[node] > 0: continue
            start_time = time
            cur = node
            while cur != -1 and visit_time[cur] == 0:
                visit_time[cur] = time
                time += 1
                cur = edges[cur]
            if cur != -1 and visit_time[cur] >= start_time:
                ans = max(ans, time - visit_time[cur])
        return ans

> [name=Yen-Chi Chen][time=Sun, Mar 26, 2023]

class Solution:
    def longestCycle(self, edges: List[int]) -> int:
        max_length = -1
        global_visited = set()
        for start, edge in enumerate(edges):
            visited_node = {}
            pos = 0
            node = start
            while edges[node] != -1:
                visited_node[node] = pos
                node = edges[node]
                if node in visited_node:
                    length = pos - visited_node[node] + 1
                    if length > max_length:
                        max_length = length
                    break
                if node in global_visited:
                    break
                pos += 1
                global_visited.add(node)
            global_visited.add(start)

        return max_length

> visited_node 原本ㄉ資料結構選錯一直TLEㄏ[name=gpwork4u][time=Sun, Mar 26, 2023]

class Solution:
    def longestCycle(self, edges: List[int]) -> int:
        n = len(edges)
        
        inDegree = [0] * n
        for edge in edges:
            if edge != -1:
                inDegree[edge] += 1

        visited = [False] * n

        # Topological Sort
        q = deque()
        for node in range(n):
            if inDegree[node] == 0:
                q.append(node)

        while q:
            node = q.popleft()
            visited[node] = True
            nei = edges[node]
            if nei != -1:
                inDegree[nei] -= 1
                if inDegree[nei] == 0:
                    q.append(nei)

        ans = -1
        for node in range(n):
            if not visited[node]:
                visited[node] = True
                nei = edges[node]
                cnt = 1
                # Iterate in the cycle
                while node != nei:
                    visited[nei] = True
                    nei = edges[nei]
                    cnt += 1
                ans = max(ans, cnt)

        return ans

> 照著 Reference 的影片做出來ㄉ
> [name=Ron Chen][time=Mon, Mar 27, 2023]

#### Javascript

function longestCycle(edges) {
  const visited = new Array(edges.length).fill(false);
  const indegree = new Array(edges.length).fill(0);
  for (const edge of edges) {
    indegree[edge]++;
  }

  const stack = [];
  for (let i = 0; i < indegree.length; i++) {
    if (indegree[i] === 0) {
      stack.push(i);
    }
  }

  while (stack.length) {
    const node = stack.pop();
    visited[node] = true;
    indegree[edges[node]]--;
    if (indegree[edges[node]] === 0) {
      stack.push(edges[node]);
    }
  }

  let ans = -1;
  for (let i = 0; i < edges.length; i++) {
    if (visited[i]) continue;
    let count = 0;
    let node = i;
    while (!visited[node]) {
      visited[node] = true;
      node = edges[node];
      count++;
    }

    ans = Math.max(ans, count);
  }

  return ans;
}

> 照著一行超人給的影片做出來惹
> [name=Marsgoat][time=Mar 30, 2023]

### Reference
[【每日一题】LeetCode 2360. Longest Cycle in a Graph](https://www.youtube.com/watch?v=_eeiFV137pw)

[回到題目列表](https://hackmd.io/@Marsgoat/leetcode_every_day)