2359.Find Closest Node to Given Two Nodes
===

###### tags: `Medium`,`DFS`,`Graph`

[2359. Find Closest Node to Given Two Nodes](https://leetcode.com/problems/find-closest-node-to-given-two-nodes/)

### 題目描述
You are given a **directed** graph of n nodes numbered from `0` to `n - 1`, where each node has **at most one** outgoing edge.

The graph is represented with a given **0-indexed** array `edges` of size `n`, indicating that there is a directed edge from node `i` to node `edges[i]`. If there is no outgoing edge from `i`, then `edges[i] == -1`.

You are also given two integers `node1` and `node2`.

Return *the **index** of the node that can be reached from both* `node1` *and* `node2`, *such that the **maximum** between the distance from* `node1` *to that node, and from* `node2` *to that node is **minimized***. If there are multiple answers, return the node with the **smallest** index, and if no possible answer exists, return `-1`.

Note that `edges` may contain cycles.

### 範例

**Example 1:**


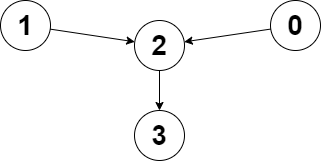
Input: edges = [2,2,3,-1], node1 = 0, node2 = 1
Output: 2
Explanation: The distance from node 0 to node 2 is 1, and the distance from node 1 to node 2 is 1.
The maximum of those two distances is 1. It can be proven that we cannot get a node with a smaller maximum distance than 1, so we return node 2.

**Example 2:**


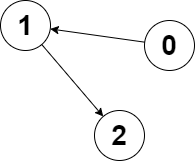
Input: edges = [1,2,-1], node1 = 0, node2 = 2
Output: 2
Explanation: The distance from node 0 to node 2 is 2, and the distance from node 2 to itself is 0.
The maximum of those two distances is 2. It can be proven that we cannot get a node with a smaller maximum distance than 2, so we return node 2.

**Constraints**:

* `n` == `edges.length`
* 2 <= `n` <= 10^5^
* -1 <= `edges[i]` < `n`
* `edges[i]` != `i`
* 0 <= `node1`, `node2` < `n`

### 解答
#### C++

class Solution {
public:
    int closestMeetingNode(vector<int>& edges, int node1, int node2) {
        int n = edges.size();
        vector<int> d1(n, INT_MAX);
        int cur = node1, step = 0;
        while (cur != -1 && d1[cur] == INT_MAX) {
            d1[cur] = step++;
            cur = edges[cur];
        }
        vector<int> d2(n, INT_MAX);
        cur = node2;
        step = 0;
        while (cur != -1 && d2[cur] == INT_MAX) {
            d2[cur] = step++;
            cur = edges[cur];
        }
        int ans = -1, upper = INT_MAX;
        for (int i = 0; i < n; i++) {
            int d = max(d1[i], d2[i]);
            if (d < upper) {
                upper = d;
                ans = i;
            }
        }
        return ans;
    }
};

> [name=Yen-Chi Chen][time=Wed, Jan 25, 2023]
#### Python

class Solution:
    def closestMeetingNode(self, edges: List[int], node1: int, node2: int) -> int:
        node_count = len(edges)
        inf = float('INF')
        d1 = [inf] * node_count
        dist = 0
        cur = node1
        
        while (cur != -1 and d1[cur] == inf):
            d1[cur] = dist
            dist+=1
            cur = edges[cur]

        d2 = [inf] * node_count
        dist = 0
        cur = node2

        while (cur != -1 and d2[cur] == inf):
            d2[cur] = dist
            dist+=1
            cur = edges[cur]
    
        maxDist = inf
        wanted_node = -1
        for node in range(node_count):
            tempDist = max(d1[node], d2[node])
            if tempDist < maxDist:
                maxDist = tempDist
                wanted_node = node
        return wanted_node

> [name=Dan][time=Sun, Jan 29, 2023]

class Solution:
    def closestMeetingNode(self, edges: List[int], node1: int, node2: int) -> int:

        while (edges[node1] >= 0 or edges[node2] >= 0):
            # mark -3 if visited by node1 loop
            # mark -2 if visited by node2 loop
            if (edges[node1] >= 0):
                temp = node1
                node1 = edges[node1]
                edges[temp] = -3
            if (edges[node2] >= 0):
                temp = node2
                node2 = edges[node2]
                edges[temp] = -2
            
            if edges[node1] == -2 and edges[node2] == -3:
                return min(node1, node2)
            elif edges[node1] == -2:
                return node1
            elif edges[node2] == -3:
                return node2

        return -1 if node1!=node2 else node1
        

> [name=Dan][time=Sun, Jan 29, 2023]

### Reference

[回到題目列表](https://hackmd.io/@Marsgoat/leetcode_every_day)