2316.Count Unreachable Pairs of Nodes in an Undirected Graph
===

###### tags: `Medium`,`DFS`,`BFS`,`Graph`

[2316. Count Unreachable Pairs of Nodes in an Undirected Graph](https://leetcode.com/problems/count-unreachable-pairs-of-nodes-in-an-undirected-graph/)

### 題目描述

You are given an integer `n`. There is an **undirected** graph with `n` nodes, numbered from `0` to `n - 1`. You are given a 2D integer array edges where `edges[i]` = [$a_i$, $b_i$] denotes that there exists an **undirected** edge connecting nodes $a_i$ and $b_i$.

Return *the **number of pairs** of different nodes that are **unreachable** from each other*.

### 範例

**Example 1:**


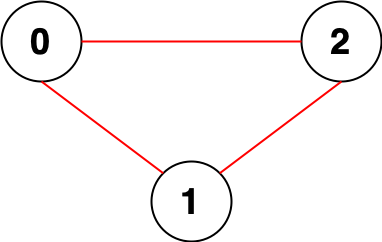
Input: n = 3, edges = [[0,1],[0,2],[1,2]]
Output: 0
Explanation: There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.

**Example 2:**


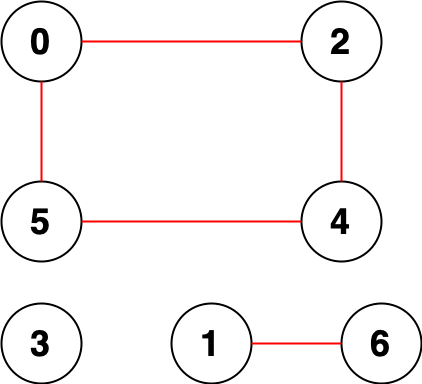
Input: n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
Output: 14
Explanation: There are 14 pairs of nodes that are unreachable from each other:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]].
Therefore, we return 14.

**Constraints**:

* 1 <= `n` <= 10^5^
* 0 <= `edges.length` <= 2 * 10^5^
* `edges[i].length` == 2
* 0 <= $a_i$, $b_i$ < `n`
* $a_i$ != $b_i$
* There are no repeated edges.

### 解答
#### Python

class Solution:
    def countPairs(self, n: int, edges: List[List[int]]) -> int:
        graph = defaultdict(list)
        for a, b in edges:
            graph[a].append(b)
            graph[b].append(a)
        
        visits = set()
        def dfs(node):
            visits.add(node)
            count = 1
            for child in graph[node]:
                if child in visits: continue
                count += dfs(child)
            return count
        
        ans = 0
        for i in range(n):
            if i in visits: continue
            c = dfs(i)
            ans += c * (n - c)
        return ans // 2

> [name=Yen-Chi Chen][time=Sat, Mar 25, 2023]

class Solution:
    def countPairs(self, n: int, edges: List[List[int]]) -> int:
        ans = n * (n - 1) // 2
        graph = defaultdict(list)

        for u, v in edges:
            graph[u].append(v)
            graph[v].append(u)

        visited = set()

        def dfs(node):
            if node in visited:
                return 0

            visited.add(node)

            cnt = 1
            for nei in graph[node]:
                cnt += dfs(nei)
            return cnt

        components = []
        for node in range(n):
            if node not in visited:
                components.append(dfs(node))

        for k in components:
            ans -= k * (k - 1) // 2

        return ans

>[name=Ron Chen][time=Sat, Mar 25, 2023]

#### Javascript

function countPairs(n, edges) {
  const graph = new Array(n).fill(0).map(() => []);
  for (const [v1, v2] of edges) {
    graph[v1].push(v2);
    graph[v2].push(v1);
  }

  const visited = new Array(n).fill(false);

  // 找出所有連通圖，並計算每個連通圖的節點數
  const graphNodes = [];
  for (let i = 0; i < n; i++) {
    if (visited[i]) continue;
    let count = 0;
    const stack = [i];
    while (stack.length) {
      const node = stack.pop();
      if (visited[node]) continue;
      visited[node] = true;
      count++;
      for (const v of graph[node]) {
        stack.push(v);
      }
    }

    graphNodes.push(count);
  }

  // 計算所有連通圖的組合數
  let ans = 0;
  for (let i = 0; i < graphNodes.length; i++) {
    for (let j = i + 1; j < graphNodes.length; j++) {
      ans += graphNodes[i] * graphNodes[j];
    }
  }

  return ans;
}

> [name=Marsgoat][time=Mar 26, 2023]

### Reference

[回到題目列表](https://hackmd.io/@Marsgoat/leetcode_every_day)