1971.Find if Path Exists in Graph
===

###### tags: `Easy`,`DFS`,`BFS`,`Graph`

[1971. Find if Path Exists in Graph](https://leetcode.com/problems/find-if-path-exists-in-graph/)

### 題目描述

There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1` (**inclusive**). The edges in the graph are represented as a 2D integer array `edges`, where each `edges[i]` = [$u_i$, $v_i$] denotes a bi-directional edge between vertex $u_i$ and vertex $v_i$. Every vertex pair is connected by **at most one** edge, and no vertex has an edge to itself.

You want to determine if there is a **valid path** that exists from vertex `source` to vertex `destination`.

Given `edges` and the integers `n`, `source`, and `destination`, return `true` *if there is a **valid path** from `source` to `destination`, or `false` otherwise*.

### 範例

**Example 1:**


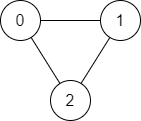
Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
- 0 → 2

**Example 2:**


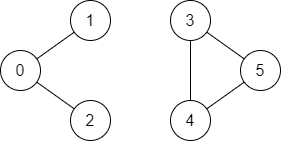
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.

**Constraints**:

* 1 <= `n` <= 2 * 10^5^
* 0 <= `edges.length` <= 2 * 10^5^
* `edges[i].length` == 2
* 0 <= $u_i$, $v_i$ <= `n - 1`
* $u_i$ != $v_i$
* 0 <= `source`, `destination` <= `n - 1`
* There are no duplicate edges.
* There are no self edges.

### 解答

#### Javascript

function validPath(n, edges, source, destination) {
  // 紀錄每個點能到的點
  const graph = [];
  for (const [v1, v2] of edges) {
    if (graph[v1] === undefined) graph[v1] = [];
    if (graph[v2] === undefined) graph[v2] = [];
    graph[v1].push(v2);
    graph[v2].push(v1);
  }

  const visited = new Array(n).fill(false);
  const stack = [source];
  while (stack.length) {
    const node = stack.pop();
    if (node === destination) return true;
    if (visited[node]) continue;
    visited[node] = true;
    for (const vertex of graph[node]) {
      stack.push(vertex);
    }
  }

  return false;
}

>[name=Marsgoat][time= Dec 19, 2022]

#### Python

class Solution:
    def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
        graph = defaultdict(dict)
        self.ans = False

        for u, v in edges:
            graph[u][v] = 1
            graph[v][u] = 1

        vis = set()
        def dfs(s, d):
            if s == d:
                self.ans = True
            for v in graph[s].keys():
                if (s, v) not in vis:
                    vis.add((s, v))
                    dfs(v, d)

        dfs(source, destination)
        return self.ans

>[name=Kobe][time= Dec 19, 2022]

class Solution:
    def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
        if source == destination:
            return True
        connected = [source]
        visited = [ 0 for x in range(n)]
        while len(connected):
            cur = connected.pop()
            visited[cur]=1

            buf =[]
            for e in edges:
                if cur == e[0] and visited[e[1]]==0 :
                    buf.append( e[1] )
                if cur == e[1] and visited[e[0]]==0:
                    buf.append( e[0] )
            
            if destination in buf:
                return True
            connected = buf + connected
            #print(buf, visited)
        return False

>[name=玉山][time= Dec 21, 2022]

#### C#

using System.Collections.ObjectModel;
public class Solution {
    public bool ValidPath(int n, int[][] edges, int source, int destination) {
        Collection<int>[] graph = CreateGraph(n, edges);

        bool[] visited = new bool[n];
        Stack<int> stack = new();
        stack.Push(source);

        while (stack.Count > 0) {
            int target = stack.Pop();
            if (target == destination) return true;
            visited[target] = true;
            foreach (var v in graph[target]) {
                if (!visited[v]) {
                    stack.Push(v);
                }
            }
        }

        return false;

        static Collection<int>[] CreateGraph(int n, int[][] edges) {
            Collection<int>[] graph = new Collection<int>[n];
            foreach (int i in Enumerable.Range(0, n)) {
                graph[i] = new Collection<int>();
            }

            foreach (int[] edge in edges) {
                graph[edge[0]].Add(edge[1]);
                graph[edge[1]].Add(edge[0]);
            }

            return graph;
        }
    }
}

>[name=Jim][time= Dec 19, 2022]
### Reference

[回到題目列表](https://hackmd.io/@Marsgoat/leetcode_every_day)