1569.Number of Ways to Reorder Array to Get Same BST
===

###### tags: `Hard`,`Math`,`Divide and Conquer`,`DP`,`Tree`,`Union Find`,`Binary Search Tree`,`Memoization`,`Combinatorics`,`Binary Tree`

[1569. Number of Ways to Reorder Array to Get Same BST](https://leetcode.com/problems/number-of-ways-to-reorder-array-to-get-same-bst/)

### 題目描述

Given an array `nums` that represents a permutation of integers from `1` to `n`. We are going to construct a binary search tree (BST) by inserting the elements of `nums` in order into an initially empty BST. Find the number of different ways to reorder `nums` so that the constructed BST is identical to that formed from the original array `nums`.

- For example, given `nums = [2,1,3]`, we will have 2 as the root, 1 as a left child, and 3 as a right child. The array `[2,3,1]` also yields the same BST but `[3,2,1]` yields a different BST.

Return *the number of ways to reorder `nums` such that the BST formed is identical to the original BST formed from `nums`.*

Since the answer may be very large, return it modulo 10⁹ + 7.

### 範例

**Example 1:**


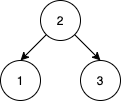
Input: nums = [2,1,3]
Output: 1
Explanation: We can reorder nums to be [2,3,1] which will yield the same BST. 
There are no other ways to reorder nums which will yield the same BST.

**Example 2:**


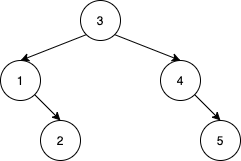
Input: nums = [3,4,5,1,2]
Output: 5
Explanation: The following 5 arrays will yield the same BST: 
[3,1,2,4,5]
[3,1,4,2,5]
[3,1,4,5,2]
[3,4,1,2,5]
[3,4,1,5,2]

**Example 3:**


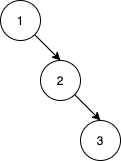
Input: nums = [1,2,3]
Output: 0
Explanation: There are no other orderings of nums that will yield the same BST.

**Constraints**:

* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= nums.length`
* All integers in `nums` are **distinct**.

### 解答

### Reference

[回到題目列表](https://hackmd.io/@Marsgoat/leetcode_every_day)