1557.Minimum Number of Vertices to Reach All Nodes
===

###### tags: `Medium`,`Graph`

[1557. Minimum Number of Vertices to Reach All Nodes](https://leetcode.com/problems/minimum-number-of-vertices-to-reach-all-nodes/)

### 題目描述

Given a **directed acyclic graph**, with `n` vertices numbered from `0` to `n-1`, and an array `edges` where `edges[i]` = [$from_i$, $to_i$] represents a directed edge from node $from_i$ to node $to_i$.

Find *the smallest set of vertices from which all nodes in the graph are reachable.* It's guaranteed that a unique solution exists.

Notice that you can return the vertices in any order.

### 範例

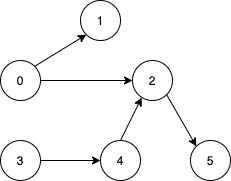
**Example 1:**


Input: n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
Output: [0,3]
Explanation: It's not possible to reach all the nodes from a single vertex. From 0 we can reach [0,1,2,5]. From 3 we can reach [3,4,2,5]. So we output [0,3].

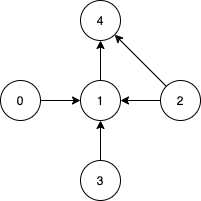
**Example 2:**


Input: n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]
Output: [0,2,3]
Explanation: Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.

**Constraints**:

* 2 <= `n` <= 10^5^
* 1 <= `edges.length` <= min(10^5^, n * (n - 1) / 2)
* `edges[i].length` == 2
* 0 <= $from_i$, $to_i$ < `n`
* All pairs ($from_i$, $to_i$) are distinct.

### 解答
#### Python

class Solution:
    def findSmallestSetOfVertices(self, n: int, edges: List[List[int]]) -> List[int]:
        return list(set(range(n)) - set(to for _, to in edges))

> [name=Yen-Chi Chen][time=Thu, May 18, 2023]

#### Javascript

function findSmallestSetOfVertices(n, edges) {
  const set = new Set();
  for (const [from, to] of edges) {
    set.add(to);
  }

  const result = [];
  for (let i = 0; i < n; i++) {
    if (!set.has(i)) result.push(i);
  }

  return result;
}

> 這題直接用Set來記錄就行了，讓我想到1579題，當時天真的以為用Set就可以ㄏㄏ
> [name=Marsgoat][time=Thu, May 18, 2023]

### Reference

[回到題目列表](https://hackmd.io/@Marsgoat/leetcode_every_day)