1519.Number of Nodes in the Sub-Tree With the Same Label
===
###### tags: `Medium`,`Tree`,`DFS`,`BFS`,`Counting`
[1519. Number of Nodes in the Sub-Tree With the Same Label](https://leetcode.com/problems/number-of-nodes-in-the-sub-tree-with-the-same-label/)
### 題目描述
You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i]` = [$a_i$, $b_i$], which means there is an edge between nodes $a_i$ and $b_i$ in the tree.
Return *an array of size* `n` where `ans[i]` is the number of nodes in the subtree of the i^th^ node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
### 範例
**Example 1:**
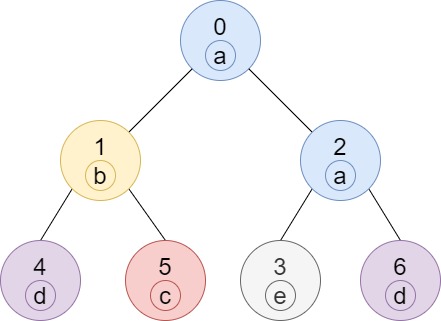
```
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"
Output: [2,1,1,1,1,1,1]
Explanation: Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
```
**Example 2:**
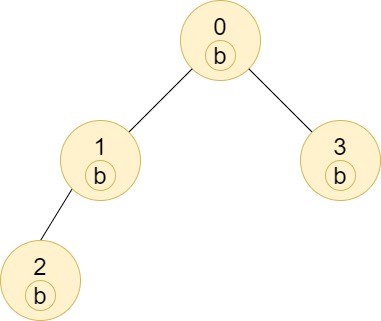
```
Input: n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"
Output: [4,2,1,1]
Explanation: The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
```
**Example 3:**
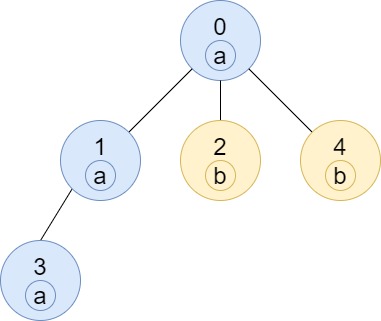
```
Input: n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"
Output: [3,2,1,1,1]
```
**Constraints**:
* 1 <= `n` <= 10^5^
* `edges.length` == `n - 1`
* `edges[i].length` == 2
* 0 <= $a_i$, $b_i$ < `n`
* $a_i$ != $b_i$
* `labels.length` == `n`
* `labels` is consisting of only of lowercase English letters.
### 解答
#### Python
```python=
class Solution:
def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:
def merge_two_dicts(x, y):
z = x.copy() # start with keys and values of x
for k,v in y.items():
if k in z:
z[k] += v
else:
z[k] = v
return z
def dfs(node):
cur_stat = dict()
cur_stat[ labels[node] ] = 1
self.ans[node] = 1
#print('#',node, self.edge[node])
for child in self.edge[node]:
#print(node,child)
if self.visited[child] == 1:
continue
self.visited[child] = 1
cur_stat = merge_two_dicts(cur_stat, dfs(child))
self.ans[node] = cur_stat[ labels[node] ]
#print(node, cur_stat)
return cur_stat
self.ans = dict()
self.edge = dict()
for i in range(n):
self.edge[i] = []
for src,dest in edges:
self.edge[src].append(dest)
self.edge[dest].append(src)
self.visited = [ 0 for _ in range(n)]
self.visited[0]= 1
root_stat = dfs(0)
self.ans[0] = root_stat[labels[0]]
return [ self.ans[i] for i in range(n)]
```
> [name=玉山]
```python=
class Solution:
def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:
tree = defaultdict(list)
for a, b in edges:
tree[a].append(b)
tree[b].append(a)
ans = [0] * n
def dfs(node, parent = -1):
count = Counter()
for child in tree[node]:
if child == parent: continue
count += dfs(child, node)
count[labels[node]] += 1
ans[node] = count[labels[node]]
return count
dfs(0)
return ans
```
> [name=Yen-Chi Chen][time=Fri, Jan 13, 2023]
### Reference
[回到題目列表](https://hackmd.io/@Marsgoat/leetcode_every_day)