1443.Minimum Time to Collect All Apples in a Tree
===

###### tags: `Medium`,`Tree`,`DFS`,`BFS`,`Hash Table`

[1443. Minimum Time to Collect All Apples in a Tree](https://leetcode.com/problems/minimum-time-to-collect-all-apples-in-a-tree/)

### 題目描述

Given an undirected tree consisting of `n` vertices numbered from `0` to `n-1`, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. *Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at **vertex 0** and coming back to this vertex*.

The edges of the undirected tree are given in the array `edges`, where `edges[i]` = [$a_i$, $b_i$] means that exists an edge connecting the vertices $a_i$ and $b_i$. Additionally, there is a boolean array hasApple, where `hasApple[i]` = `true` means that vertex `i` has an apple; otherwise, it does not have any apple.

### 範例

**Example 1:**


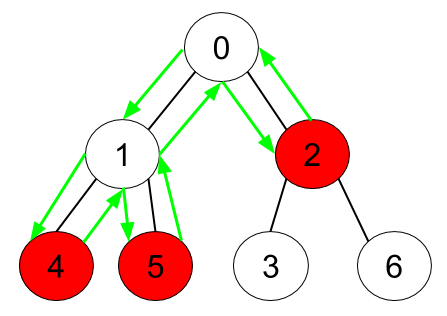
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8 
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

**Example 2:**


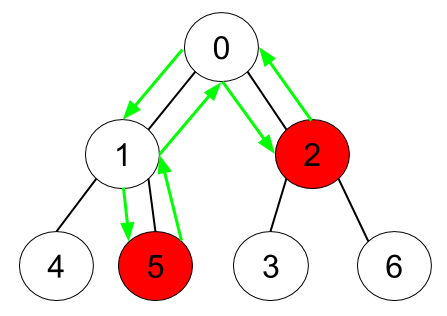
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
Output: 6
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

**Example 3:**

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
Output: 0

**Constraints**:

* 1 <= `n` <= 10^5^
* `edges.length` == `n` - 1
* `edges[i].length` == 2
* 0 <= $a_i$ < $b_i$ <= `n` - 1
* $from_i$ < $to_i$
* `hasApple.length` == `n`

### 解答
#### Javascript

function minTime(n, edges, hasApple) {
  const graph = new Array(n).fill(0).map(() => []);
  for (const [v1, v2] of edges) {
    graph[v1].push(v2);
    graph[v2].push(v1);
  }

  return dfs(0, -1, graph, hasApple);
}

function dfs(node, parent, graph, hasApple) {
  let totalTime = 0;
  let childTime = 0;
  for (const child of graph[node]) {
    if (child === parent) continue;
    childTime = dfs(child, node, graph, hasApple);
    if (childTime || hasApple[child]) {
      totalTime += childTime + 2;
    }
  }

  return totalTime;
}

>參考官網的解答寫的，第一次寫直接做dfs掃過一遍把有遇到蘋果的距離直接乘2，忘記會重複計算，有夠蠢。
>[name=Marsgoat][time=Feb 20, 2023]

### Reference

[回到題目列表](https://hackmd.io/@Marsgoat/leetcode_every_day)