1339.Maximum Product of Splitted Binary Tree
===

###### tags: `Medium`,`Tree`,`Binary Tree`,`DFS`

[1339. Maximum Product of Splitted Binary Tree](https://leetcode.com/problems/maximum-product-of-splitted-binary-tree/)

### 題目描述

Given the `root` of a binary tree, split the binary tree into two subtrees by removing one edge such that the product of the sums of the subtrees is maximized.

Return the *maximum product of the sums of the two subtrees*. Since the answer may be too large, return it **modulo** 10^9^ + 7.

**Note** that you need to maximize the answer before taking the mod and not after taking it.

### 範例

**Example 1:**


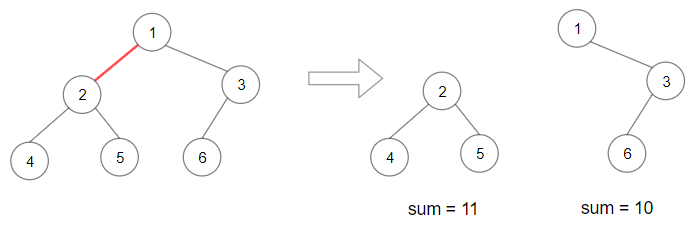
Input: root = [1,2,3,4,5,6]
Output: 110
Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)

**Example 2:**


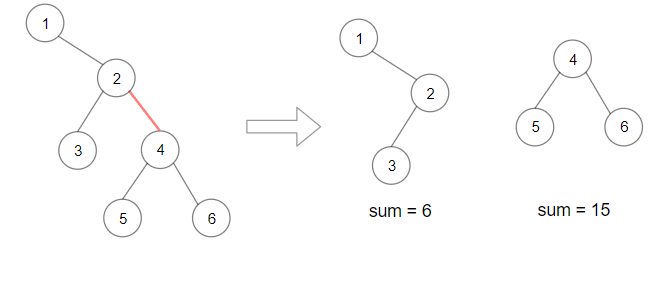
Input: root = [1,null,2,3,4,null,null,5,6]
Output: 90
Explanation: Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)

**Constraints**:

* The number of nodes in the tree is in the range [2, 5 * 10^4^].
* 1 <= `Node.val` <= 10^4^

### 解答
#### C++

class Solution {
public:
    long long result, total;
    long long dfs(TreeNode* root) {
        if (!root) return 0;
        if (root->left == root->right) return root->val;
        long long l_sum = dfs(root->left);
        long long r_sum = dfs(root->right);
        result = max(result, (total - l_sum) * l_sum);
        result = max(result, (total - r_sum) * r_sum);
        return root->val + l_sum + r_sum;
    }
    int maxProduct(TreeNode* root) {
        total = dfs(root);
        dfs(root);
        return result % 1000000007;
    }
};

> [name=Yen-Chi Chen][time=Sat, Dec 10, 2022]

#### Python

class Solution:
    def maxProduct(self, root: Optional[TreeNode]) -> int:
        all_sums = []
        def get_tree_sum(root):
            if not root: return 0

            left_sum = get_tree_sum(root.left)
            right_sum = get_tree_sum(root.right)
            total_sum = root.val + left_sum + right_sum

            all_sums.append(total_sum)
            return total_sum

        best = 0
        total = get_tree_sum(root)
        for s in all_sums:
            best = max(best, (total - s) * s)

        return best % (10 ** 9 + 7)

> [name=Kobe][time=Sun, Dec 11, 2022]
### Reference

[回到題目列表](https://hackmd.io/@Marsgoat/leetcode_every_day)