1326.Minimum Number of Taps to Open to Water a Garden
===

###### tags: `Hard` `Array` `DP` `Greedy`

[1326. Minimum Number of Taps to Open to Water a Garden](https://leetcode.com/problems/minimum-number-of-taps-to-open-to-water-a-garden/)

### 題目描述

There is a one-dimensional garden on the x-axis. The garden starts at the point `0` and ends at the point `n`. (i.e The length of the garden is `n`).

There are `n + 1` taps located at points `[0, 1, ..., n]` in the garden.

Given an integer `n` and an integer array `ranges` of length `n + 1` where `ranges[i]` (0-indexed) means the `i-th` tap can water the area `[i - ranges[i], i + ranges[i]]` if it was open.

Return *the minimum number of taps* that should be open to water the whole garden, If the garden cannot be watered return **-1**.

### 範例

**Example 1:**


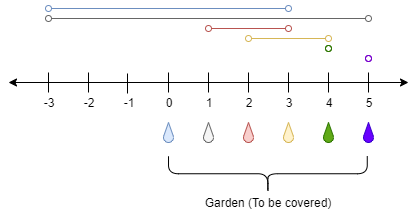
Input: n = 5, ranges = [3,4,1,1,0,0]
Output: 1
Explanation: The tap at point 0 can cover the interval [-3,3]
The tap at point 1 can cover the interval [-3,5]
The tap at point 2 can cover the interval [1,3]
The tap at point 3 can cover the interval [2,4]
The tap at point 4 can cover the interval [4,4]
The tap at point 5 can cover the interval [5,5]
Opening Only the second tap will water the whole garden [0,5]

**Example 2:**

Input: n = 3, ranges = [0,0,0,0]
Output: -1
Explanation: Even if you activate all the four taps you cannot water the whole garden.

**Constraints**:

* 1 <= `n` <= 10^4^
* `ranges.length` == `n + 1`
* 0 <= `ranges[i]` <= 100

### 解答

#### C#

public class Solution {
    public int MinTaps(int n, int[] ranges) {
        int[][] intervals = new int[n + 1][];
        for (int i = 0; i <= n; i++) {
            intervals[i] = new int[] {
                Math.Max(0, i - ranges[i]), 
                Math.Min(n, i + ranges[i]) 
            };
        }

        Array.Sort(intervals, (a, b) => a[0].CompareTo(b[0]));

        int currentMaxCoverPosition = 0;
        int searchingMaxCoverPosition = 0;

        int ans = 0;

        for (int i = 0; i <= n; i++) {
            // 有空隙無法澆到水
            if (intervals[i][0] > currentMaxCoverPosition) {
                // 沒有找到可以填滿空隙的水龍頭
                if (intervals[i][0] > searchingMaxCoverPosition) return -1;

                ans++;
                currentMaxCoverPosition = searchingMaxCoverPosition;
            }

            searchingMaxCoverPosition = Math.Max(searchingMaxCoverPosition, intervals[i][1]);
            if (searchingMaxCoverPosition == n) {
                return ++ans;
            }
        }

        return -1;
    }
}

難得這兩天的 Hard 都可以很快想到解法，看解答 intervals 可以只用一維存，晚點再改
>[name=Jim][time=Aug 31, 2023]
### Reference

[回到題目列表](https://marsgoat.github.io/XNnote/coding/leetcodeEveryDay.html)