1319.Number of Operations to Make Network Connected
===

###### tags: `Medium`,`DFS`,`BFS`,`Graph`

[1319. Number of Operations to Make Network Connected](https://leetcode.com/problems/number-of-operations-to-make-network-connected/)

### 題目描述

There are `n` computers numbered from `0` to `n - 1` connected by ethernet cables `connections` forming a network where `connections[i]` = [$a_i$, $b_i$] represents a connection between computers $a_i$ and $b_i$. Any computer can reach any other computer directly or indirectly through the network.

You are given an initial computer network `connections`. You can extract certain cables between two directly connected computers, and place them between any pair of disconnected computers to make them directly connected.

Return *the minimum number of times you need to do this in order to make all the computers connected*. If it is not possible, return `-1`.

### 範例

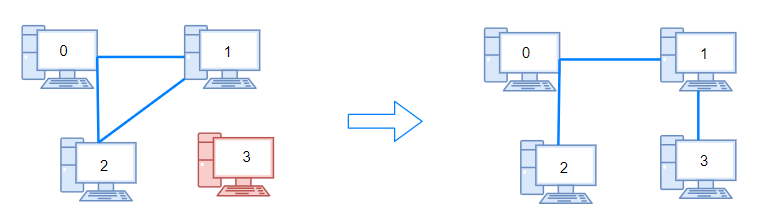
**Example 1:**


Input: n = 4, connections = [[0,1],[0,2],[1,2]]
Output: 1
Explanation: Remove cable between computer 1 and 2 and place between computers 1 and 3.

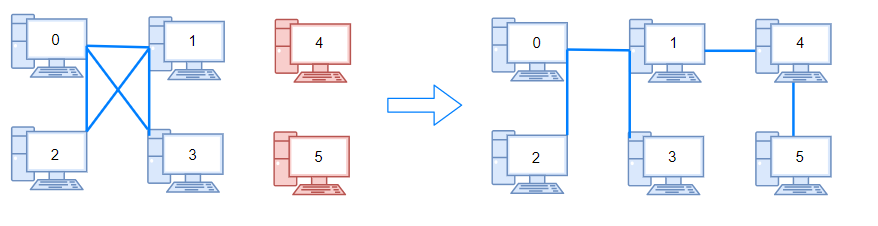
**Example 2:**


Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
Output: 2

**Example 3:**

Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2]]
Output: -1
Explanation: There are not enough cables.

**Constraints**:

* 1 <= `n` <= 10^5^
* 1 <= `connections.length` <= min(n * (n - 1) / 2, 10^5^)
* `connections[i].length` == 2
* 0 <= $a_i$, $b_i$ < `n`
* $a_i$ != $b_i$
* There are no repeated connections.
* No two computers are connected by more than one cable.

### 解答
#### Python

class Solution:
    def makeConnected(self, n: int, connections: List[List[int]]) -> int:
        if len(connections) < n - 1:
            return -1

        graph = defaultdict(list)
        for u, v in connections:
            graph[u].append(v)
            graph[v].append(u)

        components = 0
        visited = set()

        def dfs(node):
            visited.add(node)
            for nei in graph[node]:
                if nei not in visited:
                    dfs(nei)

        for i in range(n):
            if i not in visited:
                dfs(i)
                components += 1

        return components - 1

> [name=Ron Chen][time=Thu, Mar 23, 2023]

class Solution:
    def makeConnected(self, n: int, connections: List[List[int]]) -> int:
        if len(connections) < n - 1:
            return -1
        sets_tag = [i for i in range(n)]
        sets = {
            i: {i}
            for i in range(n)
        }
        count = 0
        for conn in connections:
            if sets_tag[conn[0]] == sets_tag[conn[1]]:
                continue
            sets[sets_tag[conn[0]]] |= sets[sets_tag[conn[1]]]
            replace_tag = sets_tag[conn[1]]
            for i in sets[sets_tag[conn[1]]]:
                sets_tag[i] = sets_tag[conn[0]]
            sets[replace_tag] = set()
        group_count = 0
        for s in sets.values():
            if len(s) > 0:
                group_count += 1
        return group_count - 1

>[name=gpwork4u][time=Fri, Mar 24, 2023]
#### Javascript

function makeConnected(n, connections) {
  if (connections.length < n - 1) return -1;

  const graph = new Array(n).fill(0).map(() => []);
  for (const [v1, v2] of connections) {
    graph[v1].push(v2);
    graph[v2].push(v1);
  }

  const visited = new Array(n).fill(false);
  let count = 0;

  // 從每台電腦出發開始找
  for (let i = 0; i < n; i++) {
    if (visited[i]) continue;
    count++;
    const stack = [i];
    // 標記相連的電腦
    while (stack.length) {
      const node = stack.pop();
      if (visited[node]) continue;
      visited[node] = true;
      for (const vertex of graph[node]) {
        stack.push(vertex);
      }
    }
  }

  return count - 1;
}

> [name=Marsgoat][time=Thu, Mar 23, 2023]

### Reference

[回到題目列表](https://hackmd.io/@Marsgoat/leetcode_every_day)