1289.Minimum Falling Path Sum II
===

###### tags: `Hard`,`Array`,`DP`,`Matrix`

[1289. Minimum Falling Path Sum II](https://leetcode.com/problems/minimum-falling-path-sum-ii/)

### 題目描述

Given an `n x n` integer matrix `grid`, return *the minimum sum of a **falling path with non-zero shifts***.

A **falling path with non-zero shifts** is a choice of exactly one element from each row of `grid` such that no two elements chosen in adjacent rows are in the same column.

### 範例

**Example 1:**


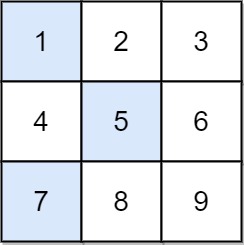
Input: arr = [[1,2,3],[4,5,6],[7,8,9]]
Output: 13
Explanation: 
The possible falling paths are:
[1,5,9], [1,5,7], [1,6,7], [1,6,8],
[2,4,8], [2,4,9], [2,6,7], [2,6,8],
[3,4,8], [3,4,9], [3,5,7], [3,5,9]
The falling path with the smallest sum is [1,5,7], so the answer is 13.

**Example 2:**

Input: grid = [[7]]
Output: 7

**Constraints**:

* `n` == `grid.length` == `grid[i].length`
* 1 <= `n` <= 200
* -99 <= `grid[i][j]` <= 99

### 解答
#### Javascript

$O(n^3)$

function minFallingPathSum(grid) {
  if (grid.length === 1) return grid[0][0];
  for (let i = 1; i < grid.length; i++) {
    for (let j = 0; j < grid.length; j++) {
      grid[i][j] += Math.min(...grid[i - 1].filter((_, index) => index !== j));
    }
  }

  return Math.min(...grid[grid.length - 1]);
}

> 吉神：都Hard了就是不要你寫 $O(n^3)$
> [name=Marsgoat][time= Dec 13, 2022]

$O(n^2)$

function minFallingPathSum(grid) {
  if (grid.length === 1) return grid[0][0];
  for (let i = 1; i < grid.length; i++) {
    let min = Infinity;
    let secondMin = Infinity;
    let index = 0;
    // 找出上一行的最小跟第二小的值
    for (let j = 0; j < grid.length; j++) {
      if (grid[i - 1][j] < min) {
        secondMin = min;
        min = grid[i - 1][j];
        index = j;
      } else if (grid[i - 1][j] < secondMin) {
        secondMin = grid[i - 1][j];
      }
    }

    // 更新 grid[i][j]
    for (let j = 0; j < grid.length; j++) {
      if (j === index) {
        grid[i][j] += secondMin;
      } else {
        grid[i][j] += min;
      }
    }
  }

  return Math.min(...grid[grid.length - 1]);
}

> 更新版本，跟吉神學習了，本來醜到爆的版本放到Discord給大家笑。
> [name=Marsgoat][time= Dec 16, 2022]

#### C++

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& grid) {
        int n = grid.size();
        if (n == 1) return grid[0][0];
        for (int i = 1; i < n; i++) {
            int m1 = INT_MAX, idx = -1, m2;
            for (int j = 0 ; j < n; j++) {
                int value = grid[i-1][j];
                if (value <= m1) {
                    m2 = m1;
                    m1 = value;
                    idx = j;
                } else if (value < m2) {
                    m2 = value;
                }
            }
            for (int j = 0; j < n; j++) {
                grid[i][j] += j == idx? m2 : m1;
            }
        }
        return *min_element(grid[n-1].begin(), grid[n-1].end());
    }
};

> [name=Yen-Chi Chen][time=Tue, Dec 13, 2022]

#### Python

class Solution:
    def minFallingPathSum(self, grid: List[List[int]]) -> int:
        n = len(grid)
        if n == 1: return grid[0][0]
        for i in range(1, n):
            m1, idx = math.inf, -1
            for j in range(n):
                value = grid[i-1][j]
                if value <= m1:
                    m2 = m1
                    m1 = value
                    idx = j
                elif value < m2:
                    m2 = value
            for j in range(n):
                grid[i][j] += m1 if idx != j else m2
        return min(grid[-1])

> [name=Yen-Chi Chen][time=Tue, Dec 13, 2022]
### Reference

[回到題目列表](https://hackmd.io/@Marsgoat/leetcode_every_day)