1514. Path with Maximum Probability

題目描述

You are given an undirected weighted graph of n nodes (0-indexed), represented by an edge list where edges[i] = [a, b] is an undirected edge connecting the nodes a and b with a probability of success of traversing that edge succProb[i].

Given two nodes start and end, find the path with the maximum probability of success to go from start to end and return its success probability.

If there is no path from start to end, return 0. Your answer will be accepted if it differs from the correct answer by at most 1e-5.

範例

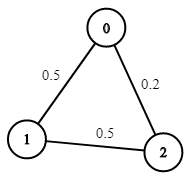
Example 1:

Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
Output: 0.25000
Explanation: There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 * 0.5 = 0.25.

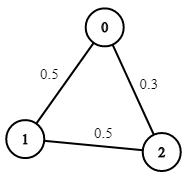
Example 2:

Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
Output: 0.30000

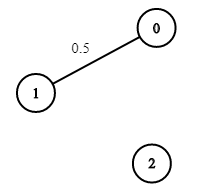
Example 3:

Input: n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
Output: 0.00000
Explanation: There is no path between 0 and 2.

Constraints:

• 2 <= n <= 10⁴
• 0 <= start, end < n
• start != end
• 0 <= a, b < n
• a != b
• 0 <= succProb.length == edges.length <= 2*10⁴
• 0 <= succProb[i] <= 1
• There is at most one edge between every two nodes.

解答

C++

class Solution {
public:
    const double INF = numeric_limits<double>::max();
    double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start, int end) {
        vector<double> distance(n, INF);
        vector<int> adj[n];
        vector<vector<double>> logProb(n, vector<double>(n, INF));
        for (int i = 0; i < edges.size(); i ++) {
            int u = edges[i][0];
            int v = edges[i][1];
            adj[u].push_back(v);
            adj[v].push_back(u);
            logProb[u][v] = -log2(succProb[i]);
            logProb[v][u] = -log2(succProb[i]);
        }

        auto cmp = [&distance](const int u, const int v) {
            return distance[u] < distance[v];
        };
        priority_queue<int, vector<int>, decltype(cmp)> frontier(cmp);
        distance[start] = 0.;
        frontier.push(start);
        while (not frontier.empty()) {
            int u = frontier.top();
            frontier.pop();
            for (int v : adj[u]) {
                if (distance[u] + logProb[u][v] < distance[v]) {
                    distance[v] = distance[u] + logProb[u][v];
                    frontier.push(v);
                }
            }
        }
        return pow(2, -distance[end]);
    }
};

Dijkstra's algorithm, TLE when n=10000

---

class Solution {
public:
    const double INF = numeric_limits<double>::max();

    double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start, int end) {
        // ios_base::sync_with_stdio(0); cin.tie(0);

        vector<vector<pair<int, double>>> adj(n);
        for (int i = 0; i < edges.size(); i ++) {
            int u = edges[i][0];
            int v = edges[i][1];
            adj[u].push_back({v, succProb[i]});
            adj[v].push_back({u, succProb[i]});
        }
        vector<double> distance(n, 0.);
        distance[start] = 1.;

        queue<int> frontier;
        frontier.push(start);
        while (not frontier.empty()) {
            int u = frontier.front();
            frontier.pop();
            for (const auto [v, prob] : adj[u]) {
                if (distance[u] * prob > distance[v]) {
                    distance[v] = distance[u] * prob;
                    frontier.push(v);
                }
            }
        }
        return distance[end];
    }
};

BFS, Beats 93.16%

Jerry28 June, 2023

Reference

回到題目列表