# TOI 2023 Problem
## 傳送門
- [一模](#一模)
- [二模](#二模)
- [三模](#三模)
- [四模](#四模)
</br></br></br></br></br></br></br></br></br></br>
## 一模
### A 國王的簽名照 (autograph) [Communication, 3s/2 GB]
有一個 $5 \times 5$ 的網格,國王會在上面走 Hamiltonian Path,每一天走一格,兩個格子相鄰若且唯若他們共用一條邊界。
你每一天可以拜訪一個點(不同天可以重複),你的目標是最大化跟國王在同一個點的天數,如果你沒遇到,那你還是能知道國王來過了沒以及什麼時候來過。
具體來說,你可以呼叫**至多** $25$ 次 `Check(`$k$`)`,第 $i$ 次呼叫表示你第 $i$ 天造訪 $k$ 號節點,而回傳的值是
- $0$,如果國王當天在那個節點
- $d$,如果國王在這天之前來過,表示國王在第 $d$ 天抵達這個節點
- $-1$,如果國王沒有來過
在一次測試中,評分程式最多呼叫這個函數 $10$ 次。
#### 範圍限制
- Judge 是 Adaptive 的。
#### 評分說明
定義你跟國王在同一地點的天數是 $K$,那你的得分是
|$K$|$0$|$1$|$[2, 8]$|$9$|$10$|$[11, 25]$|
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
|得分|$0$|$0.08$|$0.03K+0.15$|$0.51$|$0.75$|$1.0$
|分數|額外輸入限制|
|:-:|:-|
|$12$|Judge 不是 Adaptive 的
|$30$|國王從 $1$ 號節點(左上角)出發
|$14$|當天的 `Check(k)` 不會影響該次 Judge 的 Adaptive 策略
|$44$|無額外限制
### B 最佳劇照 (stills) [Batch, 1s/2 GB]
有 $n$ 個線段,第 $i$ 個是 $[l_i,r_i]$,你要找出若干個整數點覆蓋所有的線段,如果你選擇時間 $t$,則該點的**不自然度**是所有包含這個點的線段的 $|(r_i - t) - (t - l_i)|$ 的總和。
你要找到一組覆蓋的方式使得該方式所有點的**不自然度**總和最少,並且輸出其中一組最佳方案。
#### 範圍限制
- $1 \leq n \leq 10^5$
- $0 \leq l_i < r_i \leq 10^9$ 且 $l_i, r_i$ 都是偶數
#### 範例測資
輸入格式
$n$
$l_1$ $r_1$
$l_2$ $r_2$
$\vdots$
$l_n$ $r_n$
輸出格式
$S$
$k$
$t_1$
$t_2$
$\vdots$
$t_k$
|Sample Input|Sample Output|
|:-|:-|
|`5`</br>`2 10`</br>`4 8`</br>`6 18`</br>`8 16`</br>`12 16`|`8`</br>`2`</br>`5`</br>`12`</br></br></br>
|`2`</br>`2 6`</br>`4 8`</br></br>|`4`</br>`2`</br>`3`</br>`7`
#### 評分說明
定義你找到的最佳解的**不自然度**總和是 $S$,而方案是覆蓋 $t_1,t_2,\cdots,t_k$,那
- 如果 $S$ 是最佳解且方案是最佳方案,那得分是 $1.0$
- 如果 $S$ 是最佳解但方案不合法或總**不自然度**不是 $S$,那得分是 $0.6$
- 如果 $S$ 不是最佳解,那得分是 $0$。
|分數|額外輸入限制|
|:-:|:-|
|$11$|$n \leq 1000, r_i \leq 1000$
|$15$|$n \leq 1000, r_i \leq 10^7$
|$17$|$n \leq 10^5, r_i \leq 10^6, \sum_i (r_i - l_i) \leq 5 \times 10^8$
|$57$|無額外限制
### C 密碼提示系統 (guesspass) [Communication, 3s/2 GB]
有一個未知的密碼字串 $R$,長度為 $n$,包含前 $m$ 個大寫英文字母且每種至少出現一次。
你可以做出兩種詢問,兩種詢問都是給定一個嚴格遞增序列 $S$,定義 $X = R_{s_1}R_{s_2}\cdots R_{s_{|S|}}$,
- `GetCount(`$S$`)` 會回傳 $X$ 有多少種不同的字元。
- `GetRank(`$S$`)` 會回傳對於所有 $X$ 的排列來說,$X$ 是字典序第幾小的答案,但若這個答案超過 $10^{15}$,會回傳 $-1$。
兩種詢問的代價都是 $5+|S|$,總詢問代價不能超過 $200000 = 2 \times 10^5$。
在一次測試中,評分程式最多呼叫這個函數 $5$ 次。
#### 範圍限制
- $1 \leq m \leq n \leq 1000$
- $1 \leq m \leq 26$
- Judge 不是 Adaptive
#### 評分說明
假設在所有呼叫中,你的程式呼叫 `GetCount` 跟 `GetRank` 的總代價最大值是 $Q$,那你的得分 $S$ 是
$S = \begin{cases}0 & \text{if } Q > 200000\\\lfloor\frac{200000-Q}{3200}\rfloor\times 0.01 & \text{if } 40000 < Q \leq 200000\\ 0.5 + \lfloor\frac{40000-Q}{200}\rfloor\times 0.01 & \text{if } 30000 < Q \leq 40000\\1 & \text{if } Q \leq 30000\end{cases}$
|分數|額外輸入限制|
|:-:|:-|
|$3$|$n = m$
|$10$|$m = 2$
|$20$|$m \leq 10$
|$67$|無額外限制
### D 安逸旅行路線 (jaunt) [Batch, 3s/2 GB]
有一張 $n$ 點 $m$ 邊有向圖,邊 $u \rightarrow v$ 的難度係數為 $d(u, v)$,代表如果 $u \rightarrow v$ 是路徑上的第 $k$ 條邊(1-based),則這條邊的**辛苦程度**是 $d(u, v)^k\mod P$,一條路徑的辛苦程度被定義為路徑上所有邊的最大**辛苦程度**。
輸出 $s$ 到 $t$ 的所有路徑中,最小辛苦程度的值,若不存在請輸出 $-1$。
#### 範圍限制
- $1 \leq n \leq 1000$
- $1 \leq m \leq 5000$
- $2 \leq P \leq 10^5$ 且 $P$ 是質數
- $0 \leq d(u_i, v_i) < P$
- $1 \leq s, t, u_i, v_i \leq n$
- $s \neq t$
#### 範例測資
輸入格式
$n$ $m$ $P$ $s$ $t$
$u_1$ $v_1$ $d(u_1, v_1)$
$u_2$ $v_2$ $d(u_2, v_2)$
$\vdots$
$u_m$ $v_m$ $d(u_m, v_m)$
輸出格式
$ans$
|Sample Input|Sample Output|
|:-|:-|
|`3 3 11 1 3`</br>`1 2 3`</br>`2 3 2`</br>`1 3 9`|`4`</br></br></br></br>
|`3 3 11 1 3`</br>`1 2 2`</br>`2 1 1`</br>`1 3 7`|`2`</br></br></br></br>
|`3 3 11 1 3`</br>`1 2 5`</br>`2 1 1`</br>`3 1 4`|`-1`</br></br></br></br>
|`2 6 94949 1 2`</br>`1 1 2`</br>`1 2 12345`</br>`1 2 23451`</br>`1 2 34512`</br>`1 2 45123`</br>`1 2 51234`|`1391`</br></br></br></br></br></br></br>
#### 評分說明
|分數|額外輸入限制|
|:-:|:-|
|$8$|$n \leq 10, m \leq 100$
|$16$|$n \leq 100, m \leq 500$,圖沒有環
|$23$|$n \leq 100, m \leq 500$
|$53$|無額外限制
</br></br></br></br></br></br></br></br></br></br>
## 二模
### A 區間統計 (interval) [Batch, 3s/2 GB]
有 $n$ 個區間,開始與結束點 $a_i, b_i$ 都是 $1$ 到 $2n$ 中相異的整數點,且滿足開始點遞增($a_1 < a_2 < \cdots < a_n$)。定義 $c_1(i), c_2(i), c_3(i), c_4(i)$ 表示對第 $i$ 個區間而言,包含 $[a_i, b_i]$、被 $[a_i, b_i]$ 包含、與 $[a_i, b_i]$ 互斥(交集為空)以及與 $[a_i, b_i]$ 部份重疊的其他區間數量。
給定 $c_1(i), c_2(i), c_3(i), c_4(i)$,請回溯出一組合法的 $a, b$。
#### 範圍限制
- $2 \leq n \leq 3 \times 10^5$
- 對所有 $i$,$c_1(i) + c_2(i) + c_3(i) + c_4(i) = n - 1$
- 對所有輸入,保證存在一組合法的解
#### 評分說明
|分數|額外輸入限制|
|:-:|:-|
|$7$|$n \leq 7$
|$25$|$c_4(i) = 0$
|$19$|$n \leq 3000$
|$49$|無額外限制
### B 圓周拉弦 (chord) [Batch, 1s/2 GB]
有一個圓,上面有 $n$ 個等分點,連起兩個點 $i, j$ 所得到的分數是 $w_i + w_j \pmod k$,在連線只能交在端點的情況下,求最大分數。
#### 範圍限制
- $3 \leq n \leq 500$
- $2 \leq k \leq 500$
- $0 \leq w_i \leq k$
#### 評分說明
|分數|額外輸入限制|
|:-:|:-|
|$13$|$n \leq 15$
|$24$|$n \leq 100$
|$63$|無額外限制
### C 磁磚整理 (tiles) [Batch, 10s/2 GB]
\*本題有帶 grader 幫忙輸入及輸出
有一個 $n \times n$ 的網格,每格是白(`0`)或黑(`1`),且對主對角線對稱,你想要把這個網格變成這個樣子:
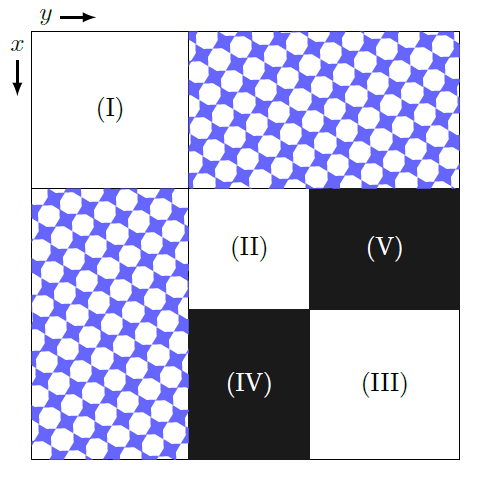
其中 $\text{I, II, III}$ 是全 `0` 的正方形,$\text{IV, V}$ 是全 `1` 的長方形,若長或寬是 $0$ 也算數(例如,全部都是白色也是一組解,因為 $\text I$ 的長寬是 $n$ 而其他的長寬都是 $0$)
你能做的操作是選擇兩個數字 $i, j$,把第 $i$ 行跟第 $j$ 行交換,再把第 $i$ 列跟第 $j$ 列交換,輸出有沒有一種操作序列可以使得網格長成上面的樣子,或決定不可能。
#### 範圍限制
- $n \leq 10000$
- 輸出的操作序列長度不得超過 $20000$
#### 評分說明
|分數|額外輸入限制|
|:-:|:-|
|$12$|$n \leq 10$
|$40$|$n \leq 500$
|$48$|無額外限制
### D 餐桌邊緣 (table) [Batch, 3s/2 GB]
空間中有一個平面 $x \in [-W, W], y \in [-L, L], z = 0$,平面的中心有個半徑為 $S$ 的球,球心在 $(0, 0, S)$,此外還有 $n$ 個圓柱與 $m$ 個圓錐,第 $i$ 個圓柱底面圓心在 $(x_i, y_i, 0)$,底面半徑是 $r_i$,高度是 $h_i$;第 $i$ 個圓錐底面圓心在 $(X_i, Y_i, 0)$,底面半徑是 $R_i$,高度是 $H_i$。
你想要把球滾到邊緣,也就是讓 $x = \pm W$ 或 $y = \pm L$,但過程中必須滿足:
- 球要接觸到桌面
- 球不能穿透桌面上的物體,但相切是可以的
- 圓柱跟圓錐不能移動
輸出最短距離,或決定不可能。輸出的絕對或相對誤差在 $10^{-6}$ 以內都視為正確。
#### 範圍限制
- $1 \leq L, W, S \leq 10000$
- $0 \leq n, m \leq 100$
- $-W \leq x_i, X_i \leq W$
- $-L \leq y_i, Y_i \leq L$
- $1 \leq r_i, h_i, R_i, H_i \leq 1000$
- 輸入的所有物體中沒有兩個互相重疊
#### 評分說明
|分數|額外輸入限制|
|:-:|:-|
|$10$|$n \leq 2, m = 0$
|$11$|$n = 0, m \leq 2$
|$20$|$m = 0, h_i$ 全相同且 $> S$
|$22$|$m = 0$
|$37$|無額外限制
</br></br></br></br></br></br></br></br></br></br>
## 三模
### A 最便宜的茶葉蛋 (Eggs) [Batch, 4s/2 GB]
有 $n$ 間商店排成一排,第 $i$ 座商店的顏色是 $c_i$,總共有 $m$ 種顏色,而第 $j$ 種顏色的商店賣茶葉蛋的價格是 $p_j$,你需要支援 $q$ 筆詢問,每筆分別是這三種其中一個:
1. 單點修改顏色
2. 單點修改某個顏色的價格
3. 區間詢問最低價格
#### 範圍限制
- $1 \leq n, m, q \leq 300\,000$
- $0 \leq c_i < m$
- $1 \leq p_j \leq 10^9$
#### 評分說明
|分數|額外輸入限制|
|:-:|:-|
|$7$|$n, m, q \leq 5000$
|$36$|$n, m \leq 20\,000$
|$40$|$n \leq 100\,000$
|$17$|無額外限制
### B 巴斯達三角形 (Pasta) [Batch, 1s/2 GB]
有一張地圖,地圖可以分成 $n$ 行,第 $x$ 行(0-based)有 $x + 1$ 個六邊形,依序編號為 $(x, 0), (x, 1), \cdots, (x, x)$,其中 $(x, y)$ 跟下一行的 $(x + 1, y), (x + 1, y + 1)$ 相鄰。
這個地圖有些地方不能通行,對 $0 \leq x < n$,而言,$(x, 0), (x, x)$ 都是可以通行的,而對於 $0 \leq x < n, 1 \leq y < i$,這個格子 $(x, y)$ 能通行若且唯若 $(x - 1, y - 1), (x - 1, y)$ 恰有一格可以通行。
你每一步可以往六邊形的六個方向走,給定 $q$ 筆 $(x, y), (z, w)$,輸出兩點間的最短路。保證兩點皆是可以通行的。
#### 範圍限制
- $2 \leq n \leq 10^{15}$
- $1 \leq q \leq 10^5$
#### 評分說明
|分數|額外輸入限制|
|:-:|:-|
|$9$|$n, q \leq 100$
|$15$|$n \leq 10^5, q \leq 100$
|$33$|$n \leq 10^5$
|$43$|無額外限制
### C 最穩定的薪水 (Salary) [Batch, 3s/2 GB]
有一棵樹,第 $i$ 個節點可能有兩種狀況:**已開發**或**發展中**,對**已開發**的城市,平均薪資固定為 $x_i$,而對於**發展中**的城市,平均薪資起始為 $x_i = 0$,而這些城市會不斷的(同時或不同時)調漲員工薪水,對這些城市而言,定義 $N(i)$ 是該點的鄰居集合而 $c_i$ 為加碼的常數,那這次薪水的調漲將會是
$\displaystyle x_i \leftarrow \max\left\{x_i, c_i + \frac 1 {|N(i)|}\sum_{j\in N(i)}x_j\right\}$
也就是鄰居的薪資平均加上加碼常數 $c_i$ 與當下的薪資取最大值。
已知在任意順序下經過無限多次的調整之後所有城市的薪資都會達到一個固定的數值,對所有**發展中**的城市輸出這個最終固定的 $x_i$。輸出的絕對或相對誤差在 $10^{-6}$ 以內都視為正確。
#### 範圍限制
- $1 \leq n \leq 10^6$
- $0 \leq$ 初始的 $x_i,c_i \leq 10^6$
#### 評分說明
|分數|額外輸入限制|
|:-:|:-|
|$17$|$n \leq 50$
|$9$|$\|N(i)\| \leq 2$
|$22$|$c_i = 0$
|$19$|$n \leq 5000$
|$33$|無額外限制
### D 眾口鑠金 (Majority) [Output Only]
有 $n$ 個布林值 $b_i\,(0 \leq i < n)$,總共有 $d$ 天,除了最後一天以外,你可以舉辦很多場投票;而在最後一天,你只能恰舉辦一場投票,而這場投票將會是最後的總決策。
每一場投票恰由 $k$ 個人參與($k$ 是奇數),每個代理人會做出贊成($1$)或反對($0$)的意見,而投票的結果將會是這些意見較多的那種。對一場發生在第 $i$ 天的投票,每個人有三種代表意見的可能:
1. 代表某個 $b_i$
2. 代表在第 $i$ 天以前發生某場投票的結果
3. 永遠是贊成或反對
注意可以有複數個代表人代表相同來源的意見。
你的目標是對於給定的 $f : [0, 2^n-1] \rightarrow \{0, 1\}$,你想要構造一種投票的過程滿足最後一天唯一一場投票的結果為 $f(\sum 2^ib_i)$。
#### 範圍限制
- $2 \leq n \leq 12$
- $3 \leq k \leq 11$ 且為奇數
- $1 \leq d \leq 8$
- 保證 $f(0) = 0, f(2^n - 1) = 1$
- 保證輸入存在一種沒有 3. 這種代表人的合法會議過程
- 總會議數量 $\leq 10000$
#### 評分說明
對每一組測試資料,若輸出合法,則你的分數是
$\dfrac S {1 + 0.3 \log_2(Q_a + Q_b + 1)}$
其中 $S$ 是該筆測試資料的得分比重,而 $Q_a$ 是 3. 的代表人總數量,$Q_b$ 是「無論 $b$ 是如何都做出相同意見的代表人」數量。
|測試資料|分數比重 $S$|說明
|:-:|:-:|:-|
|1|$10$|$n = 5, k = 5, d = 8$
|2|$10$|$n = 7, k = 11, d = 8$
|3|$10$|$n = 12, k = 9, d = 8$
|4|$10$|$n = 12, k = 7, d = 8$
|5|$10$|$n = 9, k = 3, d = 5$
|6|$10$|$n = 11, k = 3, d = 5$
|7|$10$|$n = 12, k = 3, d = 5$
|8|$10$|$n = 7, k = 5, d = 2$
|9|$10$|$n = 9, k = 7, d = 2$
|10|$10$|$n = 11, k = 9, d = 2$
</br></br></br></br></br></br></br></br></br></br>
## 四模
### A 滑雪跟拍 (Ski) [Batch 6s/2 GB]
給定長為 $n + 2$ 個點的折線,其中第 $i$ 個點為 $(x_i, y_i)$ 且 $x_i$ 嚴格遞增,對另外不在這個折線上的 $m$ 個點 $(u_i, v_i)$,對所有兩個不同的點 $(u_i, v_i)$、$(u_j, v_j)$ 連接的線段,計算這條折線在線段的兩側切換了幾次,若折線(部份)在線段上則根據最少切換的次數決定這段折線落在哪一側。
::: info
ℹ 以上的說法比較接近題本的說法,實際上的**切換次數**的定義可以參考下面的說明(這段話並沒有在題本上)
對一條線段 $S$ 來講,我們只看平面上 $x$ 座標在 $(x_0, x_{n + 1})$ (經 Clarification 確認為開區間)的點集 $A$,並且令 $S'$ 是 $S \cap A$,如果 $S' = \varnothing$ 那換邊次數被定義為 $0$。
否則,定義折線的上面叫做上面,折線的下面叫做下面,折線本身可以被算做上面或者下面,而**切換次數**就被定義為將線段 $S'$ 上的點分成上面或下面,使得從一個端點走到另一個端點的過程,換面次數最小的這個次數。
:::
#### 範圍限制
- $0 \leq n \leq 5000$
- $2 \leq m \leq 5000$
- $0 \leq x_i, y_i, u_i, v_i \leq 10^6$
- $(u_i, v_i)$ 兩兩相異
#### 評分說明
|分數|額外輸入限制|
|:-:|:-|
|$21$|$n, m \leq 100$
|$19$|$v_i$ 皆相同
|$60$|無額外限制
### B 整除序列 (Divide) [Batch 1s/2 GB]
給定長度為 $n$ 的一位數字陣列 $\langle b_i\rangle$,求出位數數量總和最少的**正整數**序列 $\langle a_i \rangle$ 滿足
- $a_i | a_{i + 1}$ 或 $a_{i + 1} | a_i$
- $a_i$ 有一位數是 $b_i$
多組解輸出任意一組皆合法。
#### 範圍限制
- $2 \leq n \leq 10^5$
- $0 \leq b_i \leq 9$
#### 評分說明
|分數|額外輸入限制|
|:-:|:-|
|$6$|$n \leq 10$
|$13$|$n \leq 100$
|$22$|$n \leq 1000$
|$59$|無額外限制
### C 集合比對 (Set) [Batch 10s/2 GB]
給定 $n$ 個正整數集合 $A_i$ 及 $m$ 個正整數集合 $Q_j$,對所有 $Q_j$ 求出有多少 $A_i$ 與它的**對稱差**大小不超過 $k$。
兩個集合 $A, B$ 的**對稱差**定義為 $A\triangle B = (A\cup B) \backslash (A\cap B)$,也就是只出現在 $A$ 或 $B$ 其一的元素所組成的集合。
#### 範圍限制
- $1 \leq n, m \leq 5000$
- $0 \leq k \leq 9$
- 所有元素皆屬於 $[1, 10^6]$
- $\sum|A_i| + \sum|Q_j| \leq 3 \times 10^6$
#### 評分說明
|分數|額外輸入限制|
|:-:|:-|
|$4$|$n, m \leq 500$ 且所有元素皆屬於 $[1, 1000]$
|$12$|所有元素皆屬於 $[1, 1000]$
|$25$|$k \leq 1$
|$23$|$A_i$ 兩兩互斥
|$36$|無額外限制
### D 掃地機器人 (Robot) [Batch 2s/2 GB]
給定 $m \times n$ 的網格,有一些位置是障礙(`#`),有一些位置是空格(`.`),求出滿足下列條件的路徑總數 $\mod 10^9 + 7$。
- 起點在 $(1, 1)$
- 終點在 $(1, 1)$
- 路徑上只有空格(`.`)
- 路徑上至少有兩個相異格子
- 不計終點時,所有格子只能被通過一次
- 不存在 $2\times 2$ 的子網格沒有被路徑通過也沒有障礙
#### 範圍限制
- $2 \leq m \leq 100$
- $2 \leq n \leq 9$
#### 評分說明
|分數|額外輸入限制|
|:-:|:-|
|$18$|$n, m \leq 5$
|$31$|$n, m \leq 7$
|$51$|無額外限制
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet