---

type: slide

---

<style>
.reveal .slides {
text-align: left;
font-size:35px;
}
</style>

## 分治

Advanced Competitive Programming
2/17

----

這堂課不會講技巧，全都是例題講解。
希望大家邊聽邊想，時不時會抽人回答問題。

---

## 例題：區間和小於t
給一個長度為$n$的序列，有幾個子區間的總和會小於$t$

$1 \leq n \leq 2*10^5$，$\left| t \right| \leq 10^{14}$

----

這題雖然有資結作法，但我們這裡用分治的方法想一下
想一下怎麼把小區間的答案轉移到大區間

----

當兩個小區間長這樣，這時候有一段連續的區間和小於$t$

----

不難發現你會用到左區間的後綴和加上右區間前綴和
這個例子為5+11


----

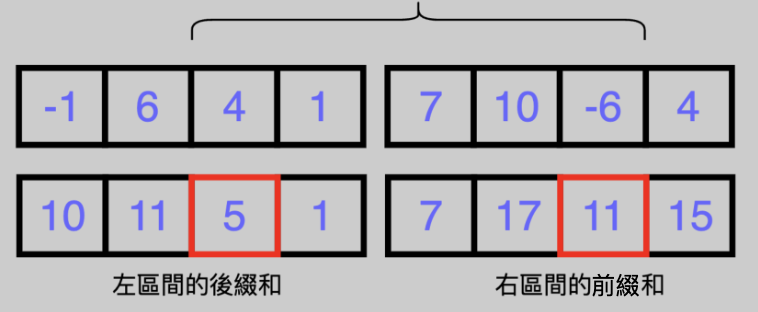
可以把左區間的後綴和排序，右區間的每個前綴和用二分搜去找左區間的有幾個後綴和可以相加<$t$

算出來的答案數量相加為答案

----

分治的難點在於要去思考小區間怎麼去計算答案，然後把小區間算答案的方式帶到大區間

接下來用更多例題帶大家思考🐳

---

## 例題：[太陽軍團(互動題)](https://neoj.sprout.tw/problem/127/)

給你一個不知道長怎樣，很大很大的$N*M$陣列，你可以多次詢問某一格的值是多少，且已知每一列的最大值出現位置都在上一列最大值的右邊，請你找出每一列的最大值出現在哪裡。
$2 \leq N \leq M \leq 10^6$，最多詢問$10^8$次


----

直接暴力$O(NM)$檢查每個格子顯然是不行的
要怎麼用分治來解這題呢，給大家幾分鐘時間想一下

----

我們可以先找中間那排，用一次$O(M)$掃過去，找最大值在哪

----

因為這題的最大值有單調性的限制，所以右上角和左下角絕對不會有最大值，剩下紅色部分的陣列要找


----

一直二分下去，複雜度是$O(MlogN)$


---

## 例題：[糟糕陣列](https://neoj.sprout.tw/problem/128/)
給你一個$N$，你要生出$N*N$的二維陣列，對於所有$i$ $(1 \leq i \leq N)$，使得「第$i$列的所有數值」和「第$i$行的所有數值」聯集起來為{$1,2,...,2N-1$}

$(1 \leq N \leq 1024)$，存在一正整數$K$使得$N=2^k$


----

一樣先想一下怎麼分治:D，你可以隨便生一個$4*4$的陣列放數字看看，也可能需要通靈一下

----

試著把一個數字放在(i,i)的位置

----

再把一個數字亂放在某個位置上，像是把2放在紅色的位置，會有以下兩種可能，那我們要取哪種呢

----

既然我們分治的觀念是解決小問題合併到大問題
那相同的小問題重複越多越好，我們寫code就不用思考太多
我們盡量把左上四塊、右下四塊長得一樣


----

無腦填3，剩下[4,5,6,7]

----

隨便填4，假設放在下面紅色的位置，會有兩種可能

----

經過一番亂填之後，上面的這兩種可能 可能會長得像這樣
看起來好像都是對的，那哪個比較好做、有規律呢？

----

對於左邊的圖，你要去紀錄左下角$2*2$方格的4,5,6,7放在哪裡
再去放右上角$2*2$方格的4,5,6,7
左下角和右上角的排列方式會不太一樣

----

反觀右邊的圖
左下角$2*2$方格只有4,5兩種數字，右上角$2*2$方格只有6,7兩種數字
並且排列方式基本一模一樣

----

既然排列方式一模一樣，不難發現這可能就是解決這題的一種方法

----

可以試試在這個二維方格切兩刀，分成四個$2*2$方格
在1~7這些數字中
選1,2,3到左上右下、4,5到左下、6,7到右上
按照規律去排數字

----

因為每次都是分成大小一樣的四塊，往下遞迴左上左下右上三塊，加上要填完所有的格子，複雜度為$O(3^{logN}+N^2)$

---

## 例題：[Max to the right Min](https://codeforces.com/problemset/problem/1849/E)

給一個長度為$n$的序列，序列為$1$~$n$的permutation，有幾個子區間符合「區間中最大的數字出現在區間中最小的數字右邊」。

----

思考時間:D
先透露這裡分治要二分，如果說兩個小區間的答案已經算完了，目前只要思考如何計算跨越兩個區間的答案就好了

可以仔細想一下有哪些case要考慮？

----

1. 最大在右邊，最小在左邊

2. 最大和最小值都在左邊

3. 最大和最小值都在右邊
你想到了嗎：D

----

不難發現你可能會需要前綴、後綴、最小值、最大值這些東西
所以我們弄出來左區間的後綴最小最大值、右區間的後綴最小最大值


----

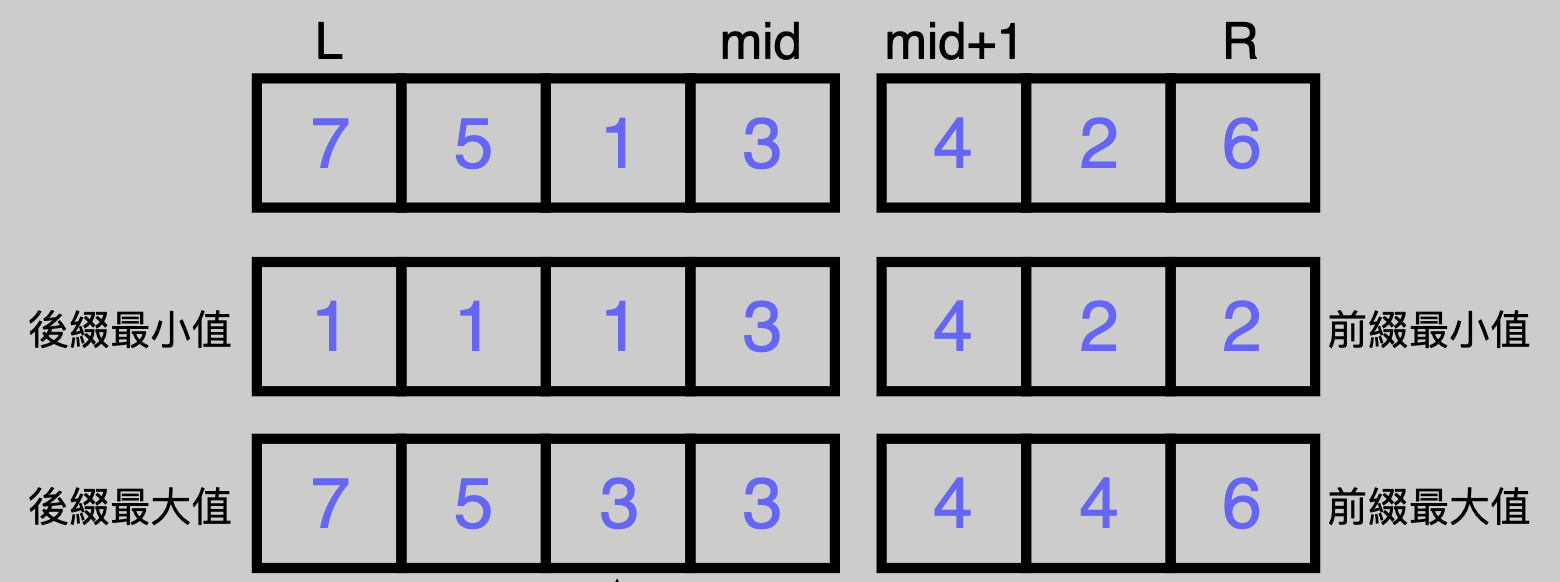
先來處理第一個case
對於一個合理的區間$[L',R']$，需要符合兩個情況

- 後綴最小值 $_{L'} <$ 前綴最小值 $_{R'}$
- 後綴最大值 $_{L'} <$ 前綴最大值 $_{R'}$


----

因為這些前綴後綴最小最大值們都有單調性，你要找符合兩個情況的數字可以用二分搜分別去找。


----

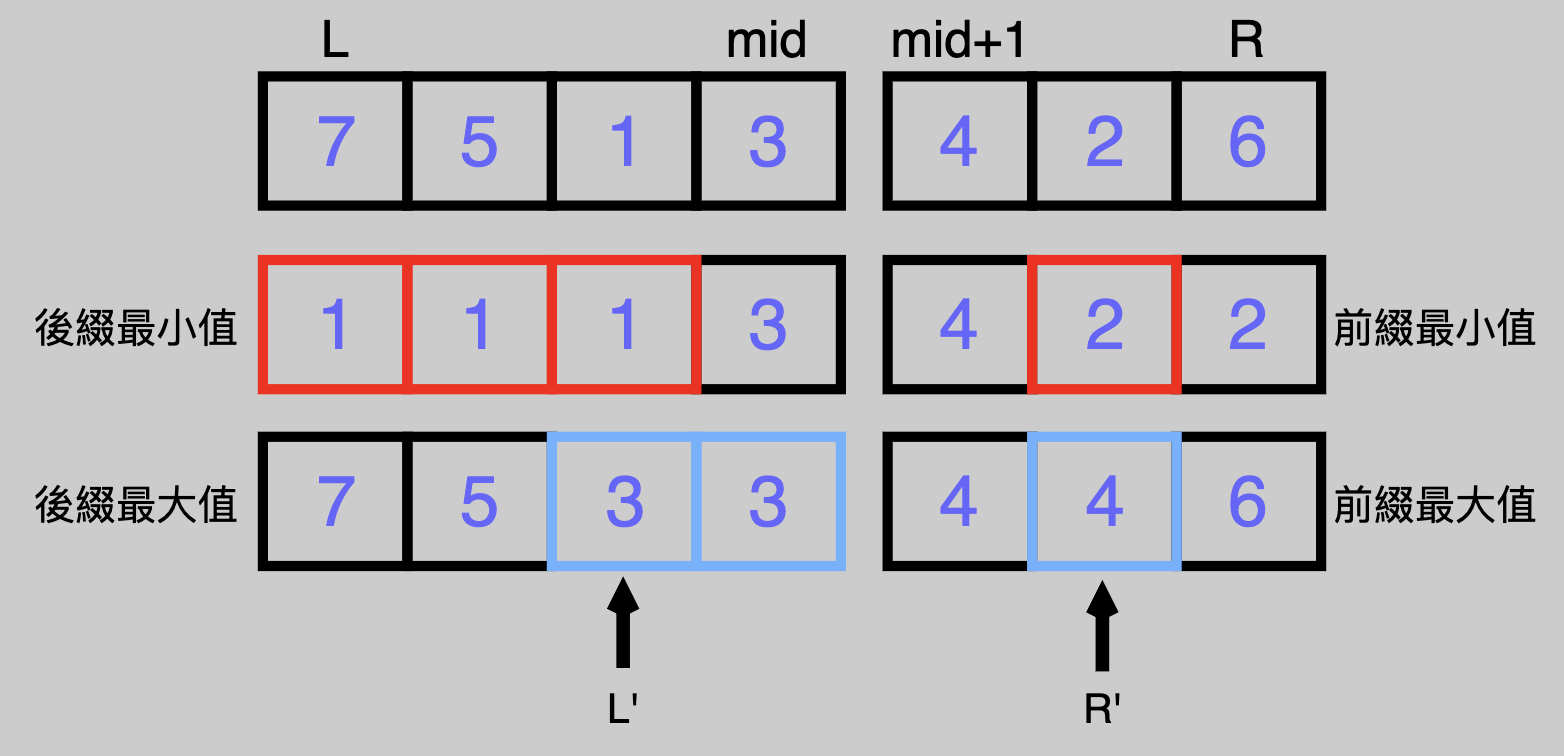
那他們交集的位置就是L'可能的位置
你可以掃過右區間的每個位置當作R'，做一遍。
這個case就解決了

----

關於第二個case，最大和最小值都在左邊，看一下合理的區間[L',R']有什麼性質

----

沒錯！！！！！就是
- 後綴最小值 $_{L'} <$ 前綴最小值 $_{R'}$
- 後綴最大值 $_{L'} >$ 前綴最大值 $_{R'}$


----

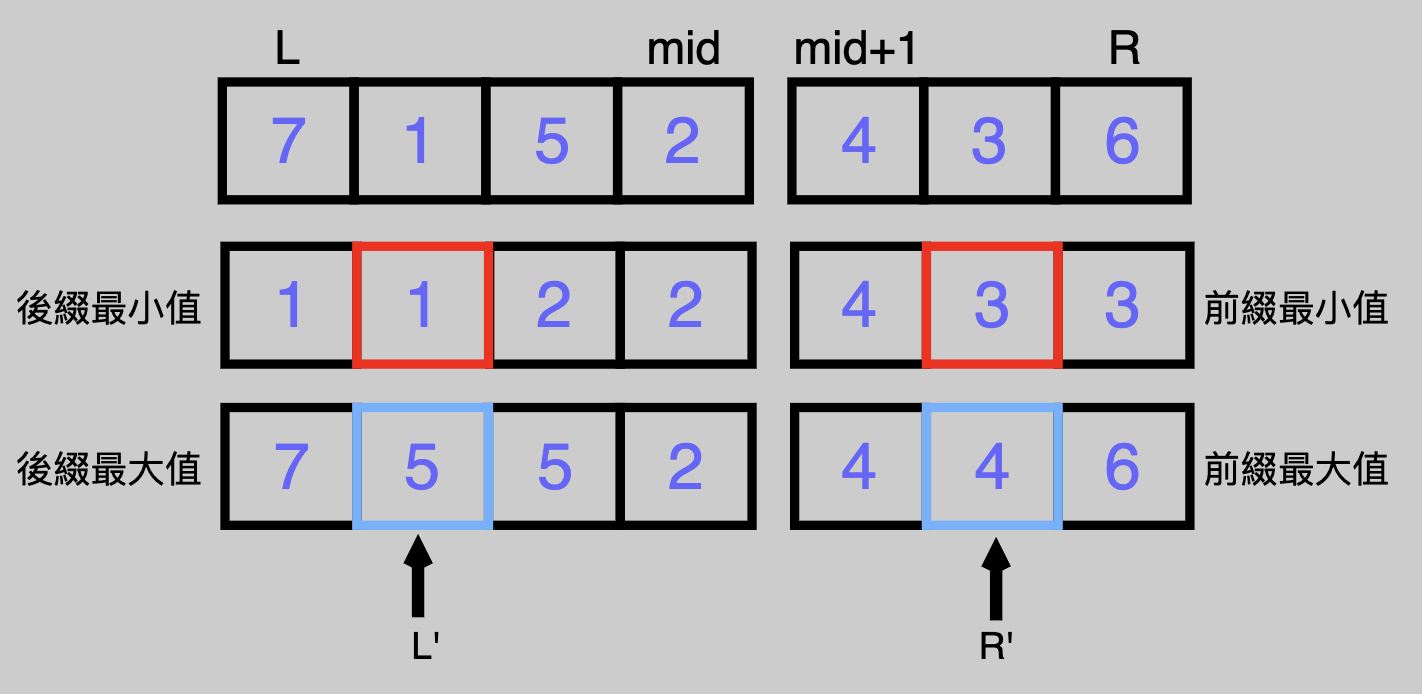
所以其實跟第一個case一樣可以利用二分搜找到交集的位置
還要多判斷左區間的Max有沒有在左區間的Min右邊
第三個case也是大同小異。

----

總體複雜度是$O(nloglogn)$，上述所講的二分搜可以用雙指針優化成$O(nlogn)$，大家可以自己想一下怎麼移指針：D

---

## 例題：[好的連續子序列😈](https://neoj.sprout.tw/problem/788/)

給一個長度為$n$的序列，序列為$1$~$n$的permutation，有幾個子區間里的元素排序之後是公差為$1$的等差數列。

$1 \leq n \leq 5\cdot 10^5$

----

一樣，思考時間:D
這裡給點提示，定義$Max$是子區間的最大值、$Min$是子區間的最小值：

- 一個區間$[L,R]$要滿足：
$R-L+1=$$Ｍax$$-$$Min$$+1=$區間長度
- 橫跨中間的子區間又要分成幾種情況？

----

誒，好像跟上一題類似，這裡分4個case

1. 最小值和最大值都在左區間

2. 最小值和最大值都在右區間

----

3. 最小值在右區間，最大值在左區間

4. 最小值在左區間，最大值在右區間

你想到了嗎：)

----

先講第一個case，講完之後你就會做第二個case了
一樣需要前綴後綴最大值最小值
用下面的區間來舉例

----

第一個case為：「最大值和最小值都在左區間」
你可以先決定一個$L'$指針代表一個合法的區間左界觀察看看
假設$L'$在下圖的這個位置

----

既然這個case叫：「最大值和最小值都在左區間」
那圖中已經赤裸裸地跟你講了最大值和最小值應該要是多少


----

提示一：$R-L+1=$$Ｍax$$-$$Min$$+1$
有了最大值、最小值、以及$L'$在哪個地方。
區間長度和、$R'$的位置就可以得出來了

----

要滿足最大值和最小值都在左邊
那右邊一定不能出現更大的值或更小的值
所以要去檢查$R'$的前綴最大值和最小值

----

經過檢查之後發現他是一個合理的區間
你可以把$L'$從$L$到$mid$計算一遍
那第二個case也是相同道理

----

好的，相對難的case要來了
接著是第三個case：「最小值在右區間，最大值在左區間」
觀察這兩個區間，用一個合理的$[L',R']$，來想想要怎麼做

----

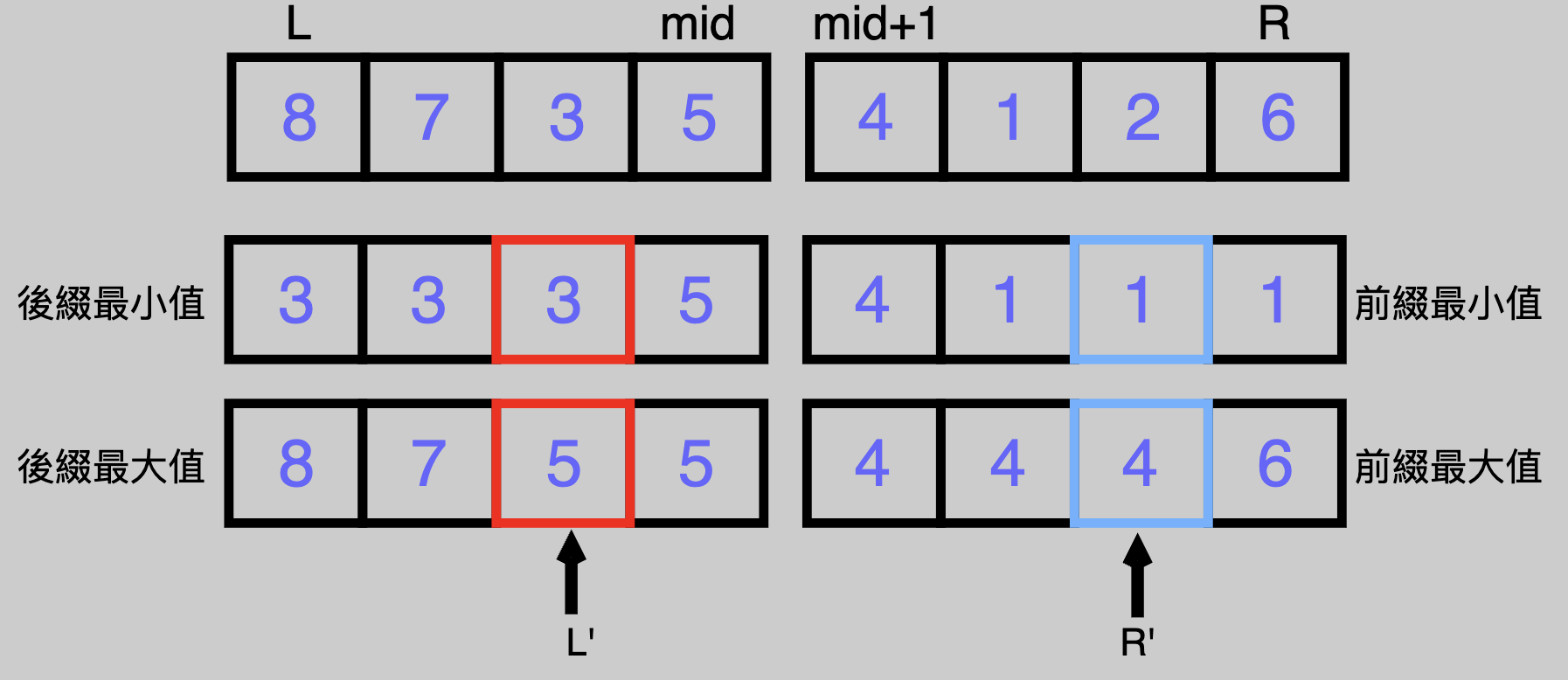
首先，既然最小值在右區間，最大值在左區間的話
代表
- 後綴最小值 $_{L'} >$ 前綴最小值 $_{R'}$
- 後綴最大值 $_{L'} >$ 前綴最大值 $_{R'}$

----

會發現好像跟上一題一樣
可以用雙指針或二分搜找到合理的區間
圖中的例子可以找到兩個合理的$R'$

----

這時候有一個問題？
兩個$R'$都可以採用嗎？
你會發現偏左的<!-- .element: class="fragment" data-fragment-index="1" -->$R'$<!-- .element: class="fragment" data-fragment-index="1" -->不能是一個合理的<!-- .element: class="fragment" data-fragment-index="1" -->$R'$<!-- .element: class="fragment" data-fragment-index="1" -->
它不滿足<!-- .element: class="fragment" data-fragment-index="1" -->$R-L+1=$<!-- .element: class="fragment" data-fragment-index="1" -->$Ｍax$<!-- .element: class="fragment" data-fragment-index="1" -->$-$<!-- .element: class="fragment" data-fragment-index="1" -->$Min$<!-- .element: class="fragment" data-fragment-index="1" -->$+1$<!-- .element: class="fragment" data-fragment-index="1" -->這個式子<!-- .element: class="fragment" data-fragment-index="1" -->

----

$R-L+1=$$Ｍax$$-$$Min$$+1$這個式子我們可以化簡成
$R+Min=L+Max$
因此我們要找哪些$R'$滿足上面這個式子

----

由於$L'$已經確定了，代表$L'+Max$為一個定值
右邊有很多種$R'+Min$，你可以用一個陣列$cnt$紀錄每種$R'+Min$的次數，然後找$cnt[L'+Max]$就好了

---

來練習8
[題目連結](https://vjudge.net/contest/605791)