# 考研筆記 - 線性代數SVD理論推導篇 (成大數學系劉育佑)
###### tags: `考研` `線性代數` `數學`
###### 撰寫時間 : 2022/08/28 ~ 2022/08/31
- 授課老師 - 成功大學數學系劉育佑教授
- 課程 - 成功大學模組化課程 奇異值分解與資料分析
## 重點1 線性轉換
### 綱要
- 抽象的線性變換藉由基底轉為歐式空間,而歐式空間的線性轉換相當於做矩陣乘法
- 特徵值是實數的線性變換 = 沿方向的伸縮變換;特徵值是複數的線性變換 = 沿方向的伸縮變換+旋轉矩陣
---
### 向量空間(vector space)與線性轉換(linear transformation)
線性代數這門學問最重要的就是在探討向量空間中線性轉換,定義向量空間最主要的2個運算為向量加法與純量乘法,再定義線性變換為一向量空間mapping到另一項向量空間的一個函數,記為$L : V \to W$,並保有以下2個線性運算的性質
1. $\mathbf{u} \cdot \mathbf{v} \in V, L(\mathbf{u} + \mathbf{v}) = L(\mathbf{u}) + L(\mathbf{u})$
2. $\alpha \in F, \mathbf{u} \in V, L(\alpha \mathbf{u}) = \alpha L(\mathbf{u})$
考慮一歐式空間的線性變換$L : \mathbb{R}^n \to \mathbb{R}^m$,將歐式空間的標準基底做線性轉換可以推導得
$$
\begin{align*}
& L(\mathbf{c}) = \mathbf{A} \mathbf{c} , \forall \mathbf{c} \in \mathbb{R}^n\\
& \text{where } \mathbf{A} = [a_{ij}]_{m \times n} \text{ : standard matrix representation of } L : \mathbb{R}^n \to \mathbb{R}^m
\end{align*}
$$
因此可以得到結論 - 歐式空間的線性變換相當於做矩陣乘法,這個矩陣稱為代表矩陣,若是以基底做線性轉換,這個矩陣可稱為標準代表矩陣。
---
### 基底(basis)與座標(coordinates)
定義基底為線性獨立的向量集,記為$E = \{\mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_n\}$且有"足夠多"的向量可以span成向量空間,記為$\mathrm{Span}(E) = V$,因此在這個向量空間中的每個向量都可以用這個基底所線性組合的係數合成,其中這個**線性組合的係數稱之為座標**
$$
\begin{align*}
& \forall \mathbf{v} \in V, \exists \mathbf{v} = c_1 \mathbf{v}_1 + c_2 \mathbf{v}_2 + \cdots + c_n \mathbf{v}_n \ldots \text{linear combination of basis}\\
& [\mathbf{v}]_{E} = \mathbf{c} = \begin{bmatrix} c_1\\ c_2\\ \vdots\\ c_n \end{bmatrix} \in F^n \ldots \text{coordinate of } \mathbf{v}
\end{align*}
$$
上述座標的form與歐式空間相似,因此有了上述基底與座標的觀念,就可以把一個有限維$\dim(V) = n$抽象的向量空間"透過基底"轉換為跟$\dim(V) = n$歐式空間相似的form。
> 需要記得是有限維數的空間,線性代數只探討有限維數的空間,至於無窮維的空間討論是泛函分析。
因此總結來說,考慮一個抽象的線性變換$L : V \to W$,透過給定抽象的向量空間$V$一組基底$E = \{\mathbf{v}_1, \ldots, \mathbf{v}_n \}$與給定抽象的向量空間$V$一組基底$F = \{\mathbf{w}_1, \ldots, \mathbf{w}_n \}$,就可以把這個兩個抽象的向量空間拉至歐式空間,而歐式空間的線性轉換等於矩陣乘法。
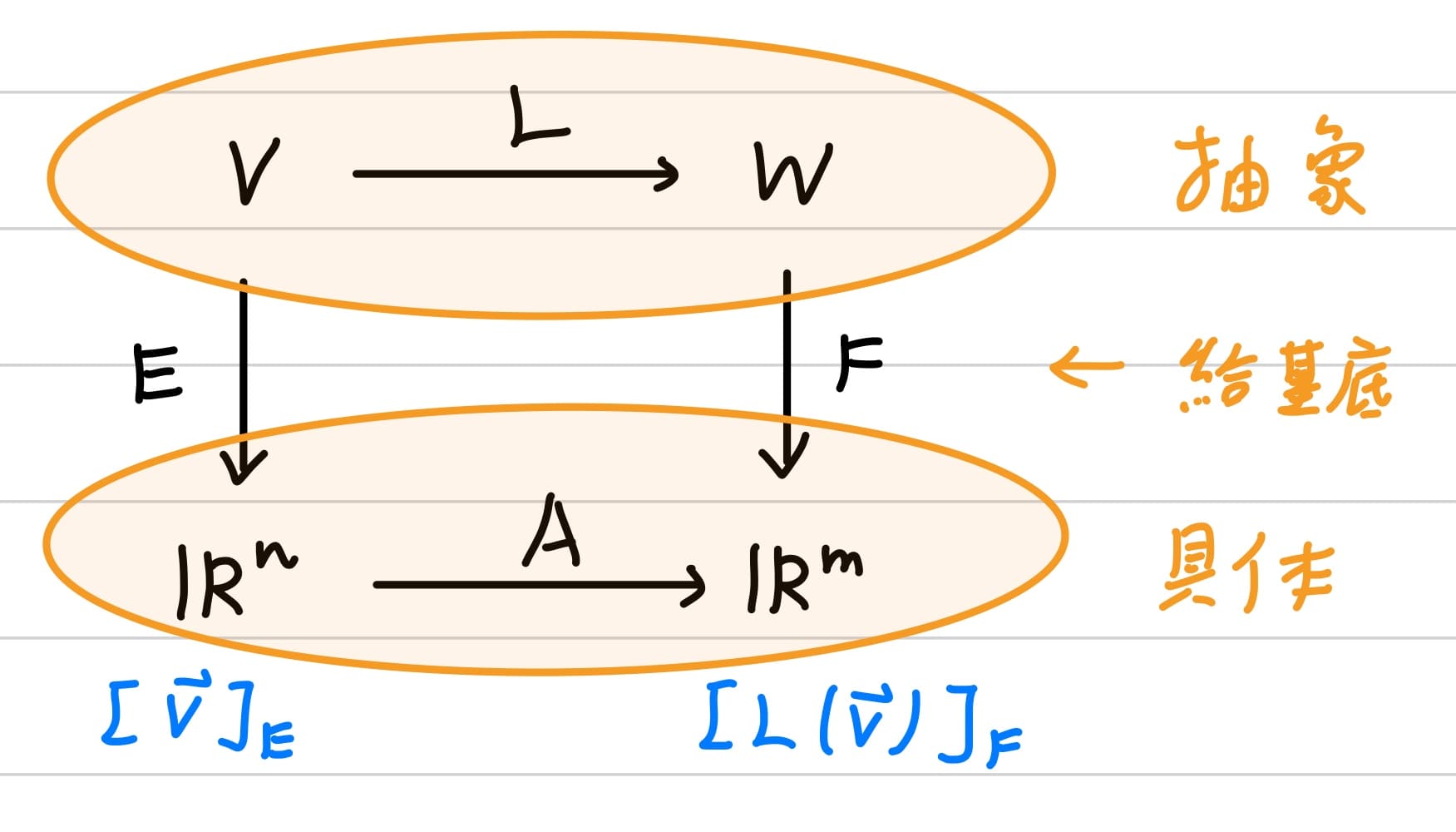
$$
\begin{align*}
& [L(\mathbf{v})]_F = \mathbf{A} [\mathbf{v}]_E, \forall \mathbf{v} \in V\\
& \text{where } \mathbf{A} = [a_{ij}]_{m \times n} \text{ : matrix representation of } L : V \to W\\
& \text{with repect to basis } E \text{ of } V \text{ and basis } F \text{ of } W
\end{align*}
$$
---
### 基底轉換與線性轉換
由於基底不具有唯一性,因此同一向量空間中不同基底之間轉換就需要乘上一個轉換的矩陣,這個矩陣就是要如何用新的基底選擇適當的線性組合合成出原基底的向量之中線性組合的係數。假設在標準基底下的代表矩陣難以計算,我們可以嘗試"繞遠路",先將標準基底轉換為"好算"的基底,這個"好算"的基底的代表矩陣十分好求,之後再將"好算"的基底轉換為標準基底即可。
---
### 特徵值/向量與對角化
特徵值/向量與對角化就是基於上述的觀念,首先把問題限制在定義域與對應域相同的線性轉換$T : V \to V$,想法是嘗試找一個"適當"的基底下使線性變換簡單,對單一向量來說這個簡單的線性就只是一個純量乘上自己$\mathbf{A} \mathbf{x} = \lambda \mathbf{x}$,而對整個向量空間來說的代表矩陣就是對角化矩陣$\mathbf{A} = \mathbf{CDC}^{-1}$。
在求向量$\mathbf{v}$的線性變換$\mathbf{Av}$時,我們有了不一樣的解題思路,嘗試把向量$\mathbf{v}$拆成各個特徵向量的線性組合
$$
\mathbf{A} (c_1 \mathbf{v}_1 + \ldots + c_n \mathbf{v}_n)
$$
再來沿著各個特徵向量的方向去做移動,也就是乘上一個scalar
$$
(c_1 \lambda_1) \mathbf{v}_1 + \ldots + (c_n \lambda_n) \mathbf{v}_n
$$
最後將這些運算完的向量一一相加就是$\mathbf{Av}$,如下圖所示
<br>
另一個觀念是當求出來的特徵值是複數的話,經過對角化後對角線矩陣是複數,形式十分複雜,我們嘗試將其轉為Canical form,就可以發現實際上$\mathbf{A} = \mathbf{CDC}^{-1}$中$\mathbf{D}$是一個伸縮加上旋轉的矩陣。總結來說特徵值是實數就只是沿特徵向量方向做伸縮變換;特徵值是複數不只是沿特徵向量方向做伸縮變換,還會旋轉。
<br>
## 重點2 正定矩陣
### 綱要
- 正定矩陣定義與等價定義的條件 - 所有特徵值皆為正數
- 正定矩陣定義與等價定義的條件 - 可被Cholesky分解、首項主子方陣大於0
- SVD分解想法與結合基底轉換與線性轉換的理解
- 計算流程 - 將半正定矩陣$\mathbf{A}^T \mathbf{A}$對角化,再利用線性轉換的關係式
---
### 正定矩陣定義
正定矩陣的先決條件為對稱矩陣$\mathbf{A} = \mathbf{A}^T \in \mathbb{R}^{n \times n}$,對所有非零的向量$\mathbf{x} \in \mathbb{R}^n$,滿足
$$
Q(x_i) = \mathbf{x}^T \mathbf{A} \mathbf{x} > 0
$$
其中$Q(x_i)$稱之為矩陣的二項式(matrix of quadratic form)。觀察上式矩陣相乘最後的size,$(1 \times n), (n \times n), (n \times 1)$會是一個純量。
---
### 正定矩陣等價條件 - 所有特徵值皆為正數
1. 證明$p \Rightarrow q$<br>
給定對稱矩陣$\mathbf{A} = \mathbf{A}^T \in \mathbb{R}^{n \times n}$,根據對稱矩陣可以實對角化的性質(證明略省),將其對角化
$$
\begin{align*}
& \mathbf{A} = \mathbf{Q} \mathbf{\Lambda} \mathbf{Q}^{-1} = \mathbf{Q} \mathbf{\Lambda} \mathbf{Q}^T\\
& \text{where } \mathbf{Q} \in \mathbb{R}^{n \times n} \text{ is orthogonal matrix}\\
& \text{and } \mathbf{\Lambda} \in \mathbb{R}^{n \times n} \text{ is diagonal matrix}\\
\end{align*}
$$
帶入正定矩陣的二次式條件$Q(x_i) = \mathbf{x}^T \mathbf{A} \mathbf{x} > 0$得
$$
\begin{align*}
\mathbf{x}^T \mathbf{A} \mathbf{x} &= \mathbf{x}^T \mathbf{Q} \mathbf{\Lambda} \mathbf{Q}^T \mathbf{x}\\
&= (\mathbf{Q}^T \mathbf{x})^T \mathbf{\Lambda} (\mathbf{Q}^T \mathbf{x})\\
\text{let } \mathbf{Q}^T \mathbf{x} &= \mathbf{y} \in \mathbb{R}^n \Rightarrow \mathbf{x} = \mathbf{Q} \mathbf{y}\\
\mathbf{x} \neq \mathbf{0} &\Leftrightarrow \mathbf{y} \neq \mathbf{0} \quad \because \mathbf{Q} \text{ is invertible matrix}\\
&= \mathbf{y}^T \mathbf{\Lambda} \mathbf{y}\\
&= \begin{bmatrix} y_1 & \cdots y_n \end{bmatrix}
\begin{bmatrix} \lambda_1 & & \mathbf{0}\\ & \ddots &\vdots\\ \mathbf{0} & & \lambda_n \end{bmatrix} \begin{bmatrix} y_1\\ \vdots\\ y_n \end{bmatrix}\\
&= \lambda_1 y_1^2 + \lambda_2 y_2^2 + \ldots + \lambda_n y_n^2
\end{align*}
$$
2. 證明$p \Leftarrow q$<br>
利用反證法,當$\lambda_i \leq 0$,令$\mathbf{x} = \mathbf{v}_i \neq \mathbf{0}$,則
$$
\mathbf{v}_i^T \mathbf{A} \mathbf{v}_i = \mathbf{v}_i^T ( \lambda_i \mathbf{v}_i) = \lambda_i \| \mathbf{v}_i \|^2 \leq 0
$$
則$\mathbf{A}$不是正定矩陣。
---
### 正定矩陣等價條件 - 可被Cholesky分解$\mathbf{A} = \mathbf{LL}^T$
| 新增條件 | 矩陣分解 |
| ------------------------ | ---------- |
| 高斯消去法時不需要列交換 | LU分解 |
| 可逆矩陣 | LDU分解 |
| 對稱矩陣 | LDL^T^分解 |
| 正定矩陣 | LL^T^分解 |
給定一**不需要列交換**的矩陣,透過"加法列運算的高斯消去法"$R_{ij}(k), i < j$,一步步化簡為row echelon form,這個row echelon form就是上三角矩陣$\mathbf{U}$,而將之前經過"加法列運算的高斯消去法"的每一步都轉換為基本矩陣,記為
$$
\mathbf{L}_3 \mathbf{L}_2 \mathbf{L}_1 \mathbf{A} = \mathbf{U} \Rightarrow \mathbf{A} = (\mathbf{L}_3 \mathbf{L}_2 \mathbf{L}_1)^{-1} \mathbf{U} = \mathbf{L}_0 \mathbf{U}
$$
加上$\mathbf{A}$為**可逆矩陣**的條件,可以推得
$$
\begin{align*}
\mathbf{A} \text{ is invertible matrix} &\Rightarrow \mathbf{U} \text{ is invertible matrix}\\
&\Rightarrow \det(\mathbf{U}) = a_{11} \cdot a_{22} \cdot \ldots \cdot a_{nn} \neq 0\\
&\Rightarrow a_{11} \neq 0, a_{22} \neq 0, \ldots, a_{nn} \neq 0
\end{align*}
$$
其中$\mathbf{U}$對角線數字均不為0,因此進一步將$\mathbf{U}$拆解為對角線矩陣$\mathbf{D}$與對角線元素為1的上三角矩陣$\mathbf{U}_0$,記為
$$
\mathbf{A} = \mathbf{L}_0 \mathbf{U} = \mathbf{L}_0 \mathbf{D} \mathbf{U}_0
$$
再加上$\mathbf{A}$為**對稱矩陣**的條件,可以推得
$$
\begin{cases}
\mathbf{A} = \mathbf{L}_0 \mathbf{D} \mathbf{U}_0\\
\mathbf{A}^T = \mathbf{U}_0^T \mathbf{D}^T \mathbf{L}_0^T
\end{cases}
\Rightarrow \mathbf{U}_0 = \mathbf{L}_0^T
\Rightarrow \mathbf{A} = \mathbf{L}_0 \mathbf{D} \mathbf{L}_0^T
$$
最後加上$\mathbf{A}$為**正定矩陣**的條件,可以推得
$$
\begin{align*}
\mathbf{x}^T \mathbf{A} \mathbf{x} &= \mathbf{x}^T (\mathbf{L}_0 \mathbf{D} \mathbf{L}_0^T) \mathbf{x}\\
&= (\mathbf{L}_0^T \mathbf{x})^T \mathbf{D} (\mathbf{L}_0^T \mathbf{x})\\
&= \mathbf{D} \| \mathbf{L}_0^T \mathbf{x})^T \|_2\\
\end{align*}
$$
由於正定矩陣的條件$\mathbf{x}^T \mathbf{A} \mathbf{x} > 0$,所以對角線矩陣每個對角線元素都會大於0,因此開根號後不會是虛數,矩陣$\mathbf{A}$就可以被進一步分解為
$$
\begin{align*}
\mathbf{A} &= \mathbf{L}_0 \mathbf{D} \mathbf{L}_0^T\\
&= \mathbf{L}_0 \sqrt{\mathbf{D}} \sqrt{\mathbf{D}}^T \mathbf{L}_0^T\\
&= (\mathbf{L}_0 \sqrt{\mathbf{D}}) (\mathbf{L}_0 \sqrt{\mathbf{D}})^T\\
&= \mathbf{L} \mathbf{L}^T \quad \text{where } \mathbf{L} = \mathbf{L}_0 \sqrt{\mathbf{D}}
\end{align*}
$$
欲證明另一邊的$p \Leftarrow q$,則將$\mathbf{L} \mathbf{L}^L$帶入正定矩陣的條件
$$
\mathbf{x}^T \mathbf{A} \mathbf{x} = \mathbf{x}^T (\mathbf{L} \mathbf{L}^T) \mathbf{x} = (\mathbf{L}^T \mathbf{x})^T (\mathbf{L}^T \mathbf{x}) = \| \mathbf{L}^T \mathbf{x}\| > 0, \forall \mathbf{x} \neq \mathbf{0}
$$
### 正定矩陣等價條件 - 首項主子方陣大於0 $\det (\mathbf{A}_i) > 0, i = 1, 2, \ldots , n$
正定矩陣其中一個等價條件為可被Cholesky分解,也就是對角線矩陣的元素皆大於0,因此
$$
\begin{align*}
&\mathbf{A} \text{ is positive definite}\\
\Leftrightarrow\; & d_1 > 0, d_2 > 0, \ldots, d_n > 0\\
\Leftrightarrow\; & d_1 > 0, d_1 d_2 > 0, \ldots, d_1 \cdots d_n > 0\\
\Leftrightarrow\; & \det(\mathbf{A}_1) > 0, \det(\mathbf{A}_2) > 0, \ldots, \det(\mathbf{A}_n) > 0\\
\end{align*}
$$
---
### SVD分解想法與結合基底轉換與線性轉換的理解
特徵值分解只適用可對角化的方陣,非對角化的方陣可以找其Jordan Form,但如果不是方陣的話就需要使用SVD(singular value decomposition)分解,SVD分解適用於任何矩陣。"仿造"前面對角化的觀念,當要求代表矩陣$\mathbf{A}$我們試圖"繞遠路",分別選擇兩組"好算"的基底為單位正交,使得在此基底下的線性轉換$\mathbf{\Sigma}$僅在對角線的前$r$項數值有值。<br>
<br>
因此SVD分解形式就可寫作為
$$
\begin{align*}
& \mathbf{A} = \mathbf{U\Sigma V}^{-1} = \mathbf{U\Sigma V}^T\\
& \text{where } \mathbf{V} = \{ \mathbf{v}_1, \ldots, \mathbf{v}_n \} \in \mathbb{R}^{n \times n}, \text{orthogonal matrix}\\
& \text{where } \mathbf{U} = \{ \mathbf{u}_1, \ldots, \mathbf{u}_n \} \in \mathbb{R}^{m \times m}, \text{orthogonal matrix}\\
& \text{where } \mathbf{\Sigma} =
\begin{bmatrix}
\sigma_1 & \cdots & \mathbf{0} & \mathbf{0}\\
\vdots & \ddots & \vdots & \mathbf{0}\\
\mathbf{0} & \cdots & \sigma_r & \mathbf{0}\\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0}
\end{bmatrix}_{m \times r}, r \leq m, n,\; \sigma_1 \geq \sigma_2 \geq \ldots \sigma_n > 0
\end{align*}
$$
嘗試改寫成以下形式
$$
\begin{align*}
&\mathbf{AV} = \mathbf{U\Sigma}\\
\Rightarrow\;& [\mathbf{A}\mathbf{v}_1, \ldots, \mathbf{A}\mathbf{v}_m]
= [\mathbf{u}_1, \ldots, \mathbf{u}_m]
\begin{bmatrix}
\sigma_1 & \cdots & \mathbf{0} & \mathbf{0}\\
\vdots & \ddots & \vdots & \mathbf{0}\\
\mathbf{0} & \cdots & \sigma_r & \mathbf{0}\\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0}
\end{bmatrix}
= [\sigma_1 \mathbf{u}_1, \ldots, \sigma_r \mathbf{u}_r, \mathbf{0}, \ldots, \mathbf{0}]
\end{align*}
$$
也就是說給定一歐式空間線性變換,其代表矩陣為
$$
\mathbf{A} : \mathbb{R}^m \to \mathbb{R}^n
$$
嘗試把向量空間$\mathbb{R}^m$的向量$\mathbf{v}_i$mapping至向量空間$\mathbb{R}^n$的向量$\mathbf{u}_i$,其中前$r$項有值,而後面的向量則直接對應到0向量。
$$
\begin{align*}
&\mathbf{A} \mathbf{v}_i = \sigma_i \mathbf{u}_i, & 1 \leq i \leq r\\
&\mathbf{A} \mathbf{u}_i = \mathbf{0} , & r + 1 \leq k \leq n
\end{align*}
$$
同理將$\mathbf{A}$取轉置得$\mathbf{A}^T\mathbf{U} = \mathbf{V\Sigma}^T$,其中歐式空間線性變換的代表矩陣$\mathbf{A}^T : \mathbb{R}^n \to \mathbb{R}^m$,其中前$r$項有值,而後面的向量則直接對應到0向量。
---
### SVD計算步驟
嘗試將$\mathbf{A}$轉置與$\mathbf{A}$相乘
$$
\begin{align*}
\mathbf{A}^T \mathbf{A} &= \mathbf{V} \mathbf{\Sigma} \mathbf{U}^T \mathbf{U} \mathbf{\Sigma}^T \mathbf{V}^T\\
&= \mathbf{V} \mathbf{\Sigma} \mathbf{\Sigma}^T \mathbf{V}^T\\
&= \mathbf{V} \mathbf{D}_\mathbf{V} \mathbf{V}^T ,\; \text{where }\mathbf{D}_\mathbf{V} = \mathbf{\Sigma} \mathbf{\Sigma}^T\\
\end{align*}
$$
欲求$\mathbf{A} = \mathbf{U\Sigma V}^T$第一步就是求$\mathbf{A}^T \mathbf{A}$(或是$\mathbf{A} \mathbf{A}^T$),並做對角化,求出來$\mathbf{A}^T \mathbf{A}$的特徵值開根號就是$\mathbf{A}$的奇異值,記為
$$
\sigma_i = \sqrt{\lambda_i}, i = 1, \ldots, r
$$
> $\mathbf{A}^T \mathbf{A}$為半正定矩陣,故其特徵值必為實數且大於等於0,特徵值開根號所得的奇異值不會是虛數。<br><br>
> 證明 - $(\mathbf{A}^T \mathbf{A})^T = \mathbf{A}^T (\mathbf{A}^T)^T = \mathbf{A}^T \mathbf{A}$,若$\mathbf{A}^T \mathbf{A} \mathbf{v} = \lambda \mathbf{v}$,則
$$
\begin{align*}
& \mathbf{v}^T (\mathbf{A}^T \mathbf{A} \mathbf{v}) = \mathbf{v}^T(\lambda \mathbf{v})\\
\Rightarrow\;& (\mathbf{A} \mathbf{v})^T(\mathbf{A} \mathbf{v}) = \lambda \mathbf{v} \mathbf{v}^T\\
\Rightarrow\;& \lambda = \frac{\| \mathbf{A} \mathbf{v} \|^2}{\| \mathbf{v} \|^2} \geq 0
\end{align*}
$$
而$\mathbf{A}^T \mathbf{A}$的特徵值對應的特徵向量,做正規化,確保特徵向量是單位長度後,拉成一行行的行向量,形成
$$
\mathbf{V} = \begin{bmatrix} \mid & \mid & \cdots & \mid\\ \mathbf{v_1} & \mathbf{v_2} & \cdots & \mathbf{v_n}\\ \mid & \mid & \cdots & \mid\end{bmatrix}
$$
根據前面向量$\mathbf{v}_i$與向量$\mathbf{u}_i$之間線性轉換的關係式
$$
\mathbf{A} \mathbf{v}_i = \sigma_i \mathbf{u}_i \Rightarrow \mathbf{u}_i = \frac{\mathbf{A} \mathbf{v}_i}{\sigma_i}
$$
求出向量$\mathbf{u}_i$,若向量$\mathbf{v}_i$的個數少於向量$\mathbf{u}_i$的個數,也就是代表矩陣是從高維歐式空間投影到低維歐式空間,根據此線性轉換的關係式求出來的會少求幾項$\mathbf{u}_i$。
我們可以嘗試選擇一組單位向量$\mathbf{x}$不平行於已知的$\mathbf{u}_i, i = 1, \ldots, (n - 1)$,使用Gram-Schmidt orthogonalization求出單位正交基底
$$
\mathbf{u}_n = \underbrace{ \mathbf{x} - (\mathbf{x}^T \mathbf{u}_1)\mathbf{u}_1 - (\mathbf{x}^T \mathbf{u}_2)\mathbf{u}_2 - \cdots - (\mathbf{x}^T \mathbf{u}_{n - 1})\mathbf{u}_{n -1} }_{\text{Gram-Schmidt orthogonalization}}
$$
以三維空間的特殊case下就是做已知向量一與向量二的外積,記為$\mathbf{u}_3 = \mathbf{u}_1 \times \mathbf{u}_2$,最後拉成一行行的行向量,形成正交矩陣
$$
\mathbf{U} = \begin{bmatrix} \mid & \mid & \cdots & \mid\\ \mathbf{u_1} & \mathbf{u_2} & \cdots & \mathbf{u_n}\\ \mid & \mid & \cdots & \mid\end{bmatrix}
$$
以上步驟就是把$\mathbb{R}^m$空間中的單位正交集合(set) $\{ \mathbf{u}_1, \ldots, \mathbf{u}_r \}, r < m$擴展到能代表$\mathbb{R}^m$空間的單位正交基底(basis) $\{ \mathbf{u}_1, \ldots, \mathbf{u}_m \}$的過程。
## 重點3 使用SVD說明線性代數的4大空間
### 綱要
- 使用SVD說明線性代數的4大空間
- 矩陣的Frobenius norm與two norm
- 低秩近似法最佳化問題 - Eckart-Young Theorem
---
### 使用SVD說明線性代數的4大空間
考慮一線性變換的代表矩陣
$$
\mathbf{A} : \mathbb{R}^n \to \mathbb{R}^m, \mathbf{A} \in \mathbb{R}^{m \times n}
$$
可將矩陣$\mathbf{A}$做SVD分解
$$
\begin{align*}
& \mathbf{A} = \mathbf{U\Sigma V}^T\\
\Rightarrow\;& \mathbf{AV} = \mathbf{U\Sigma}\\
\Rightarrow\;& \mathbf{A}(c_1 \mathbf{v}_1 + \ldots + c_r \mathbf{v}_r + c_{r + 1} \mathbf{v}_{r + 1} + \ldots + c_n \mathbf{v}_n)\\
& = (c_1 \sigma_1) \mathbf{u}_1 + \ldots + (c_n \sigma_n) \mathbf{u}_r + \mathbf{0}
\end{align*}
$$
在$\mathbf{A}$的右側乘上向量等於做行展式,其結果為$\{\mathbf{u}_1, \ldots, \mathbf{u}_r \}$這些線性獨立的向量的線性組合,因此$\mathbf{A}$的column space為
$$
\mathrm{Col}(\mathbf{A}) = \mathrm{Span}\{ \mathbf{u}_1, \mathbf{u}_2, \ldots, \mathbf{u}_r\}
$$
而null space定義為齊次聯立方程式$\mathbf{Ax} = \mathbf{0}$中所有解$\mathbf{x}$,在此就是$\{\mathbf{v}_{r + 1}, \ldots, \mathbf{v}_n \}$這些在定義域"對應到0向量"的向量,因此$\mathbf{A}$的null space為
$$
\mathrm{Null}(\mathbf{A}) = \mathrm{Span}\{ \mathbf{v}_{r + 1}, \ldots, \mathbf{v}_n \}
$$
同理,將矩陣$\mathbf{A}$的轉置,此線性變換的代表矩陣
$$
\mathbf{A}^T : \mathbb{R}^m \to \mathbb{R}^n, \mathbf{A}^T \in \mathbb{R}^{n \times m}
$$
可將矩陣$\mathbf{A}^T$做SVD分解
$$
\begin{align*}
& \mathbf{A}^T = (\mathbf{U\Sigma V}^T)^T = \mathbf{V\Sigma}^T\mathbf{U}^T\\
\Rightarrow\;& \mathbf{AU} = \mathbf{V\Sigma}\\
\Rightarrow\;& \mathbf{A}(c_1 \mathbf{u}_1 + \ldots + c_r \mathbf{u}_r + c_{r + 1} \mathbf{u}_{r + 1} + \ldots + c_n \mathbf{u}_m)\\
& = (d_1 \sigma_1) \mathbf{v}_1 + \ldots + (d_n \sigma_n) \mathbf{v}_r + \mathbf{0}
\end{align*}
$$
在$\mathbf{A}^T$的右側乘上向量等於做行展式,其結果為$\{\mathbf{v}_1, \ldots, \mathbf{v}_r \}$這些線性獨立的向量的線性組合,因此$\mathbf{A}^T$的column space,也就是$\mathbf{A}$的row space為
$$
\mathrm{Col}(\mathbf{A}^T) = \mathrm{Row}(\mathbf{A}) = \mathrm{Span}\{ \mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_r\}
$$
而null space定義為齊次聯立方程式$\mathbf{Ax} = \mathbf{0}$中所有解$\mathbf{x}$,在此就是$\{\mathbf{u}_{r + 1}, \ldots, \mathbf{u}_n \}$這些在定義域"對應到0向量"的向量,因此$\mathbf{A}^T$的null space,也就是$\mathbf{A}$的left null space為
$$
\mathrm{Null}(\mathbf{A}^T) = \mathrm{LNull}(\mathbf{A}) = \mathrm{Span}\{ \mathbf{u}_{r + 1}, \ldots, \mathbf{u}_n \}
$$
---
### 線性代數的4大空間的性質
觀察上式,要形成向量空間$\mathbb{R}^n$就是$\mathrm{Span}\{\mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_r, \mathbf{v}_{r + 1}, \ldots, \mathbf{v}_n \}$,就是將$\mathbf{A}$的row space與$\mathbf{A}$的null space兩空間的向量相加做線性組合(和空間)而成$\mathrm{RS}(\mathbf{A}) + \mathrm{Null}(\mathbf{A})$,而$\mathrm{RS}(\mathbf{A}) \cup \mathrm{Null}(\mathbf{A}) = \{ \mathbf{0} \}$,因此為直和(direct sum)空間,其中$\mathrm{RS}(\mathbf{A})$與$\mathrm{Null}(\mathbf{A})$互為正交補空間(orthogonal complement space),同理$\mathbf{A}$的column space與$\mathbf{A}$的left null space
$$
\mathrm{Row}(\mathbf{A}) \oplus \mathrm{Null}(\mathbf{A}) = \mathbb{R}^n \Rightarrow \mathrm{Row}(\mathbf{A})^\perp = \mathrm{Null}(\mathbf{A})\\
\mathrm{Col}(\mathbf{A}) \oplus \mathrm{LNull}(\mathbf{A}) = \mathbb{R}^m \Rightarrow \mathrm{Col}(\mathbf{A})^\perp = \mathrm{LNull}(\mathbf{A})\\
$$
由[ch2 秩數(rank)](https://hackmd.io/@HsuChiChen/linear_algebra#秩數rank)結論列向量獨立個數等於行向量獨立個數,因此
$$
\mathrm{rank}(\mathbf{A}) = \dim(\mathrm{Range}(\mathbf{A})) = \dim(\mathrm{Col}(\mathbf{A})) = \dim(\mathrm{Row}(\mathbf{A})) = r
$$
即可推得rank–nullity theorem
$$
\dim(\mathrm{Null}(\mathbf{A}_{m \times n})) = n - r\\
\dim(\mathrm{LNull}(\mathbf{A}_{m \times n})) = m - r
$$
下圖為圖解法,其中垂直的符號代表兩向量子空間的交集為0向量。

---
### 矩陣的Frobenius norm與two norm
在討論低秩近似法前,我們要找到如何代表兩矩陣"長得很像"的衡量標準?直覺來說就是找兩矩陣的"長度","長度"講為較專業的術語就是範數(norm),norm符合兩個性質,一是除了零矩陣的norm等於0,其他矩陣的norm必定大於0,二是符合三角不等式$\| \mathbf{A} + \mathbf{B} \leq \| \mathbf{A} \| + \| \mathbf{B} \|, \forall \mathbf{A}, \mathbf{B} \in \mathbb{R}^{m \times n}$,norm在定義上百百種,這邊只討論2種norm
1. Frobenius norm
$$
\| \mathbf{A} \|_F = \sqrt{ \sum^m_{i = 1} \sum^n_{j = 1}|a_{ij}|^2 }
$$
將矩陣所有的entries平方相加最後開根號。
<br>
經推導,在原矩陣右邊或是左邊乘上正交矩陣,不改變Frobenius norm,因此Frobenius norm即為將$\mathbf{A}$做SVD分解中所有奇異值平方相加開根號。
$$
\| \mathbf{A} \|_F = \| \mathbf{U\Sigma V}^T \|_F = \| \mathbf{\Sigma } \|_F = \sqrt{\sigma_1^2 + \ldots + \sigma_n^2}
$$
2. Spectral norm / two norm
$$
\| \mathbf{A} \|_2 = \max_{\mathbf{x} \neq 0} \frac{\| \mathbf{Ax}\|_2}{\| \mathbf{x}\|_2}
$$
線性變換前後向量長度的比例,取其中的最大值。另一種看法,可令$\| \mathbf{x} \| = 1$就是在單位圓上做線性轉換後得到橢圓等形狀,取其離原點最大的長度。
<br>
經推導,Spectral norm為將$\mathbf{A}$做SVD分解中最大的奇異值$\sigma_1$。
$$
\| \mathbf{A} \|_2 = \sigma_1
$$
---
### SVD的外積展開式與低秩近似法
SVD分解$\mathbf{A} = \mathbf{U\Sigma V}^T$中$\mathbf{A}$數值只由$\mathbf{U}$前$r$項column vector,$\mathbf{\Sigma}$前$r \times r$的方陣決定,$\mathbf{V}^T$前$r$項row vector所決定。因此若資料以SVD形式儲存,可進一步簡化為**reduced SVD**
$$
\mathbf{A}_r = \mathbf{U}_r \mathbf{\Sigma}_r \mathbf{V}_r^T\\
\mathbf{A}_{m \times n} = \mathbf{U}_{m \times r} \mathbf{\Sigma}_{r \times r} ({V}^T)_{r \times n}
$$
由[SVD計算步驟](#SVD計算步驟)可知,欲求正交矩陣$\mathbf{U}, \mathbf{V}$,是把單位正交集合(set)擴展到單位正交基底(basis),實際上擴展哪些基底不重要,也不具有唯一性,只是為了要讓$\mathbf{U}, \mathbf{V}$的行向量單位正交而形成正交矩陣而已。
如此就可以定義SVD的前$k$項外積展開式,取前將奇異值一一取出展開
$$
\mathbf{A}_k = \sigma_1 \mathbf{u}_1 \mathbf{v}_1^T + \ldots + \sigma_k \mathbf{u}_k \mathbf{v}_k^T, i \leq k \leq r
$$
其秩數$\mathrm{rank}(\mathbf{A}_k) = k$,根據Eckart-Young Theorem,在同一秩數下$\mathrm{rank}(\mathbf{B}) = k$,最接近原本$\mathbf{A}$矩陣的距離就是前$k$項外積展開式,這就是**低秩近似法(low-rank approximation)最佳化的問題**。
$$
\text{For any } \mathbf{B} \in \mathbb{R}^{m \times n} \text{ with } \mathrm{rank}(\mathbf{B}) = k\\
\text{We have } \| \mathbf{A} - \mathbf{B} \|_F \geq \| \mathbf{A} - \mathbf{A}_k \|_F\\
\text{and } \| \mathbf{A} - \mathbf{B} \|_2 \geq \| \mathbf{A} - \mathbf{A}_k \|_2
$$
因此在同一秩數$k$下,最靠近$\mathbf{A}$的矩陣就是前$k$項外積展開式$\mathbf{A}_k$。
最後就可計算相對誤差的最小值
$$
\begin{align*}
&\frac{\| \mathbf{A} - \mathbf{B} \|_F}{\| \mathbf{A} \|_F} \geq\frac{\| \mathbf{A} - \mathbf{A}_k \|_F}{\| \mathbf{A} \|_F} = \frac{\sqrt{\sigma_{k + 1}^2 + \ldots + \sigma_r^2}}{\sqrt{\sigma_1^2 + \ldots + \sigma_r^2}}\\
&\frac{\| \mathbf{A} - \mathbf{B} \|_2}{\| \mathbf{A} \|_2} \geq\frac{\| \mathbf{A} - \mathbf{A}_k \|_2}{\| \mathbf{A} \|_2} = \frac{\sigma_{k + 1}}{\sigma_1}
\end{align*}
$$
<br>
## 重點4 最小平方+範數問題
### 綱要
- 最小平方問題
- 最小範數問題
- 最小平方+範數問題
### 最小平方問題(least square problem)
考慮$\mathbf{A}_{m \times n} \mathbf{x}_{n \times 1} = \mathbf{b}_{m \times 1}$,若$m > n, \mathrm{rank}(\mathbf{A}) = n$,也就是說有效方程式$m$條,多於未知數$n$個,屬於overdetermined problem,解不存在(或是只存在一組解),但問題總不能這樣就結束,因此我們"試圖"找到一個近似解的折衷方案 - 找$\mathbf{x} \in \mathbb{R}^n$能最小化$\mathbf{Ax} -\mathbf{b}\in \mathbb{R}^{ m \times n}$的長度。
---
### 最小平方問題解法1 - 線性代數理論
<br>
在$\mathbb{R}^m$空間下
$$
\mathbf{A} \mathbf{x} = \begin{bmatrix} \mathbf{A}_1 & \mathbf{A}_2 & \cdots & \mathbf{A}_n \end{bmatrix} \begin{bmatrix} \mathbf{x}_1\\ \mathbf{x}_2\\ \vdots\\ \mathbf{x}_n \end{bmatrix} = \mathbf{x}_1 \mathbf{A}_1 + \mathbf{x}_2 \mathbf{A}_2 + \cdots + \mathbf{x}_n \mathbf{A}_n
$$
只會落在$\mathbb{R}^n$的平面,也就是$\mathrm{Col}(\mathbf{A})$,如果$\mathbf{b}$沒落在這個平面上,記為$\mathbf{b} \not\in \mathrm{Col}(\mathbf{A})$,則解不存在。這時我們希望能在這個$\mathrm{Col}(\mathbf{A})$的平面上找到一個向量,使得$\mathbf{Ax} -\mathbf{b}$的距離能短越好,記為$\min \|\mathbf{Ax} -\mathbf{b} \|$,根據幾何的知識,要讓$\mathbf{Ax} -\mathbf{b}$向量能垂直於$\mathrm{Col}(\mathbf{A})$的平面,因此
$$
\begin{align*}
&\min \|\mathbf{Ax} -\mathbf{b} \|\\
\Rightarrow\;& \mathbf{Ax} -\mathbf{b} \in \mathrm{Col}(\mathbf{A})^\perp = \mathrm{Null}(\mathbf{A}^T)\\
\Rightarrow\;& \mathbf{A}^T (\mathbf{Ax} -\mathbf{b}) = \mathbf{0}\\
\Rightarrow\;& \mathbf{A}^T \mathbf{A} \mathbf{x} = \mathbf{A}^T \mathbf{b} \quad \ldots \text{normal equation}
\end{align*}
$$
由於問題一開始假設$\mathbf{A}$是full column rank,即$\mathrm{rank}(\mathbf{A}_{m \times n}) = n$,根據性質$\mathrm{rank}(\mathbf{A}^T\mathbf{A}) = \mathrm{rank}(\mathbf{A})$,因此$\mathrm{rank}(\mathbf{A}^T \mathbf{A}) = n$,屬於full rank,$\det(\mathbf{A}^T \mathbf{A}) \neq 0$,因此矩陣$\mathbf{A}^T \mathbf{A}$可逆。最後推得
$$
\mathbf{x} = (\mathbf{A}^T \mathbf{A})^{-1} \mathbf{A}^T \mathbf{b}
$$
### 證明性質$\mathrm{rank}(\mathbf{A}^T\mathbf{A}) = \mathrm{rank}(\mathbf{A})$
證明思路為先證明零核空間相同,再根據rank–nullity theorem證明。
1. 證明$\mathrm{Null(\mathbf{A}^T\mathbf{A})} = \mathrm{Null(\mathbf{A})}$,使用左包右,右包左證明<br>
- 左包右$\mathrm{Null(\mathbf{A})} \subseteq \mathrm{Null(\mathbf{A}^T\mathbf{A})}$
$$
\begin{align*}
& \forall \mathbf{x} \in \mathrm{Null(\mathbf{A})}\\
\Rightarrow\;& \mathbf{A} \mathbf{x} = \mathbf{0}\\
\Rightarrow\;& \mathbf{A}^T \mathbf{A} \mathbf{x} = \mathbf{A}^T \mathbf{0} = \mathbf{0}\\
\Rightarrow\;& \mathbf{x} \in \mathrm{Null(\mathbf{A}^T\mathbf{A})}
\end{align*}
$$
- 右包左$\mathrm{Null(\mathbf{A}^T\mathbf{A})} \subseteq \mathrm{Null(\mathbf{A})}$
$$
\begin{align*}
& \forall \mathbf{x} \in \mathrm{Null(\mathbf{A}^T \mathbf{A})}\\
\Rightarrow\;& \mathbf{A}^T \mathbf{A} \mathbf{x} = \mathbf{0}\\
\Rightarrow\;& \mathbf{x}^T \mathbf{A}^T \mathbf{A} \mathbf{x} = \mathbf{x}^T \mathbf{0} = \mathbf{0}\\
\Rightarrow\;& (\mathbf{A} \mathbf{x})^T(\mathbf{A} \mathbf{x}) = \mathbf{0}\\
\Rightarrow\;& \| \mathbf{A} \mathbf{x} \|^2 = 0\\
\Rightarrow\;& \mathbf{A} \mathbf{x} = \mathbf{0}\\
\Rightarrow\;& \mathbf{x} \in \mathrm{Null(\mathbf{A})}
\end{align*}
$$
2. 根據rank–nullity theorem證明$\mathrm{rank}(\mathbf{A}^T\mathbf{A}) = \mathrm{rank}(\mathbf{A})$<br>
給定矩陣$\mathbf{A}_{m \times n}$,因此$(\mathbf{A}^T \mathbf{A})_{n \times n}$,由rank–nullity theorem列出聯立方程式
$$
\begin{cases}
\mathrm{nullity}(\mathbf{A}) &= \dim(\mathrm{Null}(\mathbf{A})) &= n - \mathrm{rank}(\mathbf{\mathbf{A}})\\
\mathrm{nullity}(\mathbf{A}^T \mathbf{A}) &= \dim(\mathrm{Null}(\mathbf{A}^T \mathbf{A})) &= n - \mathrm{rank}(\mathbf{A}^T\mathbf{\mathbf{A}})\\
\end{cases}
$$
由於$\mathbf{A}$和$\mathbf{A}^T \mathbf{A}$的零核空間相同$\mathrm{Null(\mathbf{A}^T\mathbf{A})} = \mathrm{Null(\mathbf{A})}$,因此零核空間維數相同$\mathrm{nullity}(\mathbf{A}) = \mathrm{nullity}(\mathbf{A}^T \mathbf{A})$,根據rank–nullity theorem關係式就可以推得$\mathrm{rank}(\mathbf{A}^T\mathbf{A}) = \mathrm{rank}(\mathbf{A})$。
---
### 最小平方問題解法2 - 微積分理論
定義一函數$\mathbf{Ax} -\mathbf{b}$為取norm的平方,這是取距離平方是為了方便運算。
$$
F : \mathbb{R}^n \to \mathbb{R}, F(\mathbf{x}) = \| \mathbf{Ax} -\mathbf{b} \|^2
$$
欲求極值,就是找critical point,對於一個多變數實函數而言,要使所有方向的一階偏導數等於0,也就是**梯度等於0**。
$$
\text{find critical point} \Rightarrow \nabla F(\mathbf{x}) \triangleq \frac{\partial F(\mathbf{x})}{\partial\mathbf{x}} = [\frac{\partial F(\mathbf{x})}{\partial x_1}, \frac{\partial F(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial F(\mathbf{x})}{\partial x_n}] = 0
$$
欲求梯度$\nabla F(\mathbf{x})$除了可以將將函數對每一項分量做偏微分,另一種較方便的解法是先求方向導數,再**根據"方向導數為梯度與該方向的內積"這個關係式求得梯度**。
$$
D_\mathbf{y} F(\mathbf{x}) = (\nabla F(\mathbf{x})) \cdot \mathbf{y} \quad\text{for any unit vector } \mathbf{y}
$$
觀察上式的form,欲求梯度,嘗試先求方向導數,並整理成一個向量跟單位方向向量的內積的form,這個向量就是梯度。
$$
\begin{align*}
D_\mathbf{y} F(\mathbf{x}) &\triangleq \lim_{\epsilon \to 0} \frac{F(\mathbf{x} + \epsilon \mathbf{y}) - F(\mathbf{x})}{\epsilon}\\
&= \lim_{\epsilon \to 0} \frac{1}{\epsilon} \left[ \| \mathbf{A} (\mathbf{x} + \epsilon \mathbf{y}) -\mathbf{b} \|^2 - \| \mathbf{A}\mathbf{x} -\mathbf{b} \|^2 \right]\\
&= \lim_{\epsilon \to 0} \frac{1}{\epsilon} \left[ \| (\mathbf{A} (\mathbf{x} -\mathbf{b}) + \epsilon \mathbf{y}) \|^2 - \| \mathbf{A}\mathbf{x} -\mathbf{b} \|^2 \right]\\
&= \lim_{\epsilon \to 0} \frac{1}{\epsilon} \left[ \| \mathbf{A}\mathbf{x} -\mathbf{b} \|^2 + 2(\mathbf{Ax} - \mathbf{b}) \cdot (\epsilon \mathbf{Ay}) + \| \epsilon \mathbf{Ay} \|^2 - \| \mathbf{A}\mathbf{x} -\mathbf{b} \|^2 \right]\\
&= 2(\mathbf{A}\mathbf{x} -\mathbf{b}) \cdot (\mathbf{Ay})\\
&= 2(\mathbf{A}\mathbf{x} -\mathbf{b})^T (\mathbf{Ay})\\
&= 2[\mathbf{A}^T (\mathbf{A}\mathbf{x} -\mathbf{b})]^T \mathbf{y}\\
&= \underbrace{ 2[\mathbf{A}^T (\mathbf{A}\mathbf{x} -\mathbf{b})] }_{\nabla F(\mathbf{x})} \cdot \mathbf{y}\\
\end{align*}
$$
故critical point即為
$$
\begin{align*}
& \text{find critical point}\\
\Rightarrow\;& \nabla F(\mathbf{x}) = 0\\
\Rightarrow\;& 2[\mathbf{A}^T (\mathbf{A}\mathbf{x} -\mathbf{b})] = 0\\
\Rightarrow\;& \mathbf{A}^T \mathbf{A}\mathbf{x} = \mathbf{A}^T \mathbf{b}
\end{align*}
$$
同法一最後推得
$$
\mathbf{x} = (\mathbf{A}^T \mathbf{A})^{-1} \mathbf{A}^T \mathbf{b}
$$
---
### 最小範數問題(least norm problem)
考慮$\mathbf{A}_{m \times n} \mathbf{x}_{n \times 1} = \mathbf{b}_{m \times 1}$,若$m < n, \mathrm{rank}(\mathbf{A}) = m$,也就是說有效方程式$m$條,多於未知數$n$個,屬於underdetermined problem,具有無限多組解,可將解拆為齊次解與特解。
$$
\mathbf{x} = \mathbf{x}_h + \mathbf{x}_p
$$
其中齊次解$\{\mathbf{x}_h \mid \mathbf{Ax}_h = \mathbf{0}\}$為$\mathbb{R}^n$的子空間,屬於null space,以下圖$\mathbb{R}^3$空間為例,就是通過原點的平面,而特解就是將此平面做平移。欲求最佳的解,加上限制項 - 要讓解的距離最小。
---
### 最小範數問題解法1 - 線性代數理論
<br>
要使$\mathbf{x} = \mathbf{x}_h + \mathbf{x}_p$的集合落在平面,要使$\mathbf{x}$的距離最小,就是讓向量$\mathbf{x}$跟平面垂直。
$$
\begin{align*}
&\min \|\mathbf{x} \|\\
\Rightarrow\;& \mathbf{x} \in \mathrm{Null}(\mathbf{A})^\perp = \mathrm{Row}(\mathbf{A}) = \mathrm{Col}(\mathbf{A}^T)\\
\Rightarrow\;& \mathbf{x} = \mathbf{A}^T \mathbf{w}\\
\Rightarrow\;& \mathbf{A} \mathbf{x} = \mathbf{A} \mathbf{A}^T \mathbf{w} = \mathbf{b}\\
\end{align*}
$$
由於問題假設$\mathrm{rank}(\mathbf{A}) = m$加上性質$\mathrm{rank}(\mathbf{A}) = \mathrm{rank}(\mathbf{A}\mathbf{A}^T)$,因此矩陣$\mathbf{A}\mathbf{A}^T$是full rank,行列式值不等於0,存在可逆矩陣$(\mathbf{A}\mathbf{A}^T)^{-1}$,因此進一步推導
$$
\begin{align*}
& \mathbf{A} \mathbf{x} = \mathbf{A} \mathbf{A}^T \mathbf{w} = \mathbf{b}\\
\Rightarrow\;& \mathbf{w} = (\mathbf{A} \mathbf{A}^T)^{-1} \mathbf{b}\\
\Rightarrow\;& \mathbf{x} = \mathbf{A}^T \mathbf{w} = \mathbf{A}^T (\mathbf{A} \mathbf{A}^T)^{-1} \mathbf{b}
\end{align*}
$$
---
### 最小範數問題解法2 - 微積分理論
定義一函數$\mathbf{x}$距離的平方,取距離平方是為了方便運算。
$$
F : \mathbb{R}^n \to \mathbb{R}, f(\mathbf{x}) = \| \mathbf{x} \|^2 = \mathbf{x}^T \mathbf{x}
$$
在限制條件$\vec{g}(\mathbf{x}) = \mathbf{Ax} - \mathbf{b} = 0$之下,欲求$\min f(\mathbf{x})$,這種帶有限制條件的極值問題,就需要使用Lagrange multiplier,把Lagrange multiplier $\mathbf{\lambda}$想像是變數,因此將**帶有限制項的單變數向量$\mathbf{x}$求極值問題,拓展為雙變數向量$\mathbf{x}, \mathbf{\lambda}$求極值問題**。需要注意這裡Lagrange multiplier $\mathbf{\lambda}$是帶有$m$條限制式的向量形式。
$$
\begin{align*}
& \min f(\mathbf{x}) \;\text{subject to } \vec{g}(\mathbf{x})\\
\Rightarrow\;& \min \left[ F(\mathbf{x}, \mathbf{\lambda}) = f(\mathbf{x}) + \mathbf{\lambda} \cdot \vec{g}(\mathbf{x}) \right]\\
\Rightarrow\;&
\begin{cases}
\nabla_{\mathbf{\lambda}}F(\mathbf{x}, \mathbf{\lambda}) = \vec{g}(\mathbf{x}) = \mathbf{0}\\
\nabla_{\mathbf{\mathbf{y}}} F(\mathbf{x}, \mathbf{\lambda}) = \nabla_{\mathbf{\mathbf{x}}} f(\mathbf{x}) + \mathbf{\lambda} \cdot \nabla_{\mathbf{x}} \vec{g}(\mathbf{x})
\end{cases}
\end{align*}
$$
由上式可以看出[Lagrange multiplier在幾何上的意義](https://www.youtube.com/watch?v=3ahgXXv-_j8),假設在向量空間$\mathbb{R}^3$,發生極值的條件為$f(\mathbf{x})$的等位曲面與$\vec{g}(\mathbf{x})$的等位曲面相切,兩個等位曲面相切,則代表兩個梯度向量會平行,彼此只會差上一個常數倍,這個常數就是Lagrange multiplier。
帶入數值計算
$$
\begin{align*}
& \min f(\mathbf{x}) = \mathbf{x}^T \mathbf{x} \;\text{subject to } \vec{g}(\mathbf{x}) = \mathbf{Ax} - \mathbf{b} = 0\\
\Rightarrow\;& \min \left[ F(\mathbf{x}, \mathbf{\lambda}) = \mathbf{x}^T \mathbf{x} + \mathbf{\lambda}^T (\mathbf{Ax} - \mathbf{b}) \right]\\
\Rightarrow\;&
\begin{cases}
\nabla_{\mathbf{\lambda}}F(\mathbf{x}, \mathbf{\lambda}) = \mathbf{Ax} - \mathbf{b} = \mathbf{0}\\
\nabla_{\mathbf{\mathbf{y}}} F(\mathbf{x}, \mathbf{\lambda}) = \;? = 0
\end{cases}
\end{align*}
$$
欲求梯度$\nabla_{\mathbf{\mathbf{y}}} F(\mathbf{x})$,同前面最小平方問題的技巧,先求方向導數,並整理成一個向量跟單位方向向量的內積的form,這個向量就是梯度。
$$
\begin{align*}
D_\mathbf{y} F(\mathbf{x}, \mathbf{\lambda}) &\triangleq \lim_{\epsilon \to 0} \frac{F(\mathbf{x} + \epsilon \mathbf{y}, \mathbf{\lambda}) - F(\mathbf{x}, \mathbf{\lambda})}{\epsilon}\\
&= \lim_{\epsilon \to 0} \frac{1}{\epsilon} \left[ \underbrace{ (\mathbf{x} + \epsilon \mathbf{y})^T (\mathbf{x} + \epsilon \mathbf{y}) }_{= \mathbf{x}^T\mathbf{x} + \epsilon \mathbf{x}^T \mathbf{y} + \epsilon^2 \mathbf{y}^T \mathbf{x} + \epsilon^2 \mathbf{y}^T \mathbf{y} } + \mathbf{\lambda}^T ( \underbrace{ \mathbf{A}(\mathbf{x} + \epsilon \mathbf{y}) }_{= \mathbf{Ax} + \epsilon \mathbf{Ay}} - \mathbf{b}) - \mathbf{x}^T \mathbf{x} - \mathbf{\lambda}^T (\mathbf{Ax} - \mathbf{b}) \right]\\
&= \lim_{\epsilon \to 0} \frac{1}{\epsilon} \left[ \epsilon \mathbf{x}^T \mathbf{y} + \epsilon \mathbf{y}^T \mathbf{x} + \epsilon^2 \mathbf{y}^T \mathbf{y} - \epsilon \mathbf{\lambda}^T \mathbf{A}\mathbf{y} \right]\\
&= 2 \mathbf{x}^T \mathbf{y} - \mathbf{\lambda}^T \mathbf{A} \mathbf{y}\\
&= (2 \mathbf{x} - \mathbf{A}^T \mathbf{\lambda})^T \mathbf{y}\\
&= \underbrace{ (2 \mathbf{x} - \mathbf{A}^T \mathbf{\lambda}) }_{\nabla_{\mathbf{\mathbf{y}}} F(\mathbf{x}, \mathbf{\lambda})} \cdot \mathbf{y}
\end{align*}
$$
解得梯度$\nabla_{\mathbf{\mathbf{y}}} F(\mathbf{x})$,因此聯立方程式為
$$
\begin{cases}
\nabla_{\mathbf{\lambda}}F(\mathbf{x}, \mathbf{\lambda}) = \mathbf{Ax} - \mathbf{b} = \mathbf{0} &(1)\\
\nabla_{\mathbf{\mathbf{y}}} F(\mathbf{x}, \mathbf{\lambda}) = 2 \mathbf{x} - \mathbf{A}^T \mathbf{\lambda} = 0 \Rightarrow \mathbf{x} = \frac{1}{2} \mathbf{A}^T \mathbf{\lambda} &(2)
\end{cases}
$$
將式(2)帶入式(1)得
$$
\mathbf{A}(\frac{1}{2} \mathbf{A}^T \mathbf{\lambda}) - \mathbf{b} = \mathbf{0} \Rightarrow \mathbf{A} \mathbf{A}^T \mathbf{\lambda} = 2\mathbf{b}
$$
由於問題假設$\mathrm{rank}(\mathbf{A}) = m$加上性質$\mathrm{rank}(\mathbf{A}) = \mathrm{rank}(\mathbf{A}\mathbf{A}^T)$,因此矩陣$\mathbf{A}\mathbf{A}^T$是full rank,行列式值不等於0,存在可逆矩陣$(\mathbf{A}\mathbf{A}^T)^{-1}$,使得
$$
\Rightarrow \mathbf{\lambda} = 2 (\mathbf{A} \mathbf{A}^T )^{-1} \mathbf{b} \tag{3}
$$
將式(3)帶回式(2)得
$$
\mathbf{x} = \frac{1}{2} \mathbf{A}^T \mathbf{\lambda} = \mathbf{A}^T (\mathbf{A} \mathbf{A}^T)^{-1} \mathbf{b}
$$
---
### 最小平方與範數問題同時發生(least square & norm problem)
考慮$\mathbf{A}_{m \times n} \mathbf{x}_{n \times 1} = \mathbf{b}_{m \times 1}$,若$\mathrm{rank}(\mathbf{A}) = r < m, n$,想要找到向量$\mathbf{x}$使得$\min \| \mathbf{Ax} - \mathbf{b} \|$,並且在這些無限多組解中找到能$\min \| \mathbf{x} \|$。
### 最小平方與範數問題同時發生解法
- 由於$\mathrm{rank}(\mathbf{A}) = r < n$,故$\mathbf{A}^T \mathbf{A}$不可逆,若使用最小平方法只能解到$\mathbf{A}^T \mathbf{A}\mathbf{x} = \mathbf{A}^T \mathbf{b}$而卡住。
- 由於$\mathrm{rank}(\mathbf{A}) = r < m$,故$\mathbf{A} \mathbf{A}^T$不可逆,若使用最小範數法只能解到$\mathbf{x} = \mathbf{A}^T \mathbf{w}, \mathbf{A} \mathbf{A}^T \mathbf{w} = \mathbf{b}$而卡住。
因此使用SVD這個好用的工具下去求解,將$\mathbf{A}$做SVD分解,再求$\| \mathbf{Ax} - \mathbf{b} \|$
$$
\begin{align*}
\| \mathbf{A} \mathbf{x} - \mathbf{b} \|
&= (\mathbf{U\Sigma V}^T) \mathbf{x} - \mathbf{b} \|\\
&= \| \mathbf{U}^T (\mathbf{U\Sigma V}^T \mathbf{x} - \mathbf{b}) \| \quad\text{where } \mathbf{U} \text{ is orthogonal matrix}\\
&= \| \mathbf{\Sigma V}^T \mathbf{x} - \mathbf{U}^T \mathbf{b} \|
\end{align*}
$$
這時再將$\mathbf{x}$做基底轉換為$\mathbf{y}$,將$\mathbf{b}$做基底轉換為$\mathbf{c}$
$$
\text{denote } \mathbf{V}^T \mathbf{x} = \mathbf{y} \in \mathbb{R}^n, \mathbf{U}^T \mathbf{b} = \mathbf{c} \in \mathbb{R}^m \quad\text{ie } \mathbf{x} = \mathbf{Vy}, \mathbf{b} = \mathbf{Uc}
$$
因此轉換為
$$
\begin{align*}
\| \mathbf{\Sigma V}^T \mathbf{x} - \mathbf{U}^T \mathbf{b} \| &= \| \mathbf{\Sigma y} - \mathbf{c} \|\\
&= \left\|
\begin{bmatrix}
\sigma_1 & \cdots & \mathbf{0} & \mathbf{0}\\
\vdots & \ddots & \vdots & \mathbf{0}\\
\mathbf{0} & \cdots & \sigma_r & \mathbf{0}\\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0}
\end{bmatrix}
\begin{bmatrix}
y_1\\ \vdots\\ \vdots\\ y_n
\end{bmatrix}
- \begin{bmatrix}
c_1\\ \vdots\\ \vdots\\ c_n
\end{bmatrix}
\right\|\\
&= \left\|
\begin{bmatrix}
\sigma_1 y_1 - c_1\\ \vdots\\ \sigma_r y_r - c_r\\ - c_{r + 1}\\ \vdots\\ c_m
\end{bmatrix}
\right\|\\
\end{align*}
$$
因此我們把$\min \| \mathbf{A} \mathbf{x} - \mathbf{b} \|$的問題,轉換為$\min \| \mathbf{\Sigma y} - \mathbf{c} \|$,其中可以變動的是解$\mathbf{x}$,而解$\mathbf{x}$經過基底轉換後變成$\mathbf{y}$,因此只有$\mathbf{y}$可變動,根據上面推導的form,把最小化$\| \mathbf{\Sigma y} - \mathbf{c} \|$就是把$r$項弄為0,選擇
$$
y_i = \sigma_i^{-1} c_i, \; 1 \leq i \leq r
$$
再滿足最小平方問題後,再來滿足最小範數問題,欲$\min \| \mathbf{x} \|$,即為$\min \| \mathbf{y} \|$,因此後面$r$項取0
$$
y_i = 0, \; r + 1 \leq i \leq n
$$
總結$\mathbf{y}$為
$$
\mathbf{y} =
\begin{bmatrix}
\sigma_1^{-1} c_1\\ \vdots\\ \sigma_r^{-1} c_r\\ 0\\ \vdots\\ 0
\end{bmatrix}_{n \times 1}
= \begin{bmatrix}
\sigma_1^{-1} & \cdots & \mathbf{0} & \mathbf{0}\\
\vdots & \ddots & \vdots & \vdots\\
\mathbf{0} & \cdots & \sigma_r^{-1} & \mathbf{0}\\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0}\\
\vdots & \vdots & \vdots & \vdots\\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0}
\end{bmatrix}_{n \times m}
\begin{bmatrix}
c_1\\ \vdots\\ c_r\\ c_{r + 1}\\ \vdots\\ c_m
\end{bmatrix}_{m \times 1} = \mathbf{\Sigma}^+ \mathbf{c}
$$
最後變數變換(基底轉換)回原本的變數
$$
\mathbf{y} = \mathbf{\Sigma}^+ \mathbf{c} \Rightarrow \mathbf{V}^{-1} \mathbf{x} = \mathbf{\Sigma}^+ \mathbf{U}^T \mathbf{b} \Rightarrow \mathbf{x} = \mathbf{V\Sigma}^+ \mathbf{U}^T \mathbf{b}
$$
---
### 總結 - 定義虛反矩陣(pseudoinverse)
給定秩數$r$的矩陣$\mathbf{A}_{m \times n}$,做奇異值分解為
$$
\mathbf{A}_{m \times n} = \mathbf{U}_{m \times m} \mathbf{\Sigma}_{m \times n} (\mathbf{V}^T)_{n \times n}, \text{ where } \mathbf{\Sigma} =
\begin{bmatrix}
\sigma_1 & \cdots & \mathbf{0} & \mathbf{0}\\
\vdots & \ddots & \vdots & \vdots\\
\mathbf{0} & \cdots & \sigma_r & \mathbf{0}\\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0}\\
\vdots & \vdots & \vdots & \vdots\\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0}
\end{bmatrix}_{m \times n}
$$
則虛反矩陣(pseudoinverse)定義為
$$
\mathbf{A}^+ = \mathbf{V}\mathbf{\Sigma}^+\mathbf{U}^T, \text{ where } \mathbf{\Sigma}^+ =
\begin{bmatrix}
\sigma_1^{-1} & \cdots & \mathbf{0} & \mathbf{0}\\
\vdots & \ddots & \vdots & \vdots\\
\mathbf{0} & \cdots & \sigma_r^{-1} & \mathbf{0}\\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0}\\
\vdots & \vdots & \vdots & \vdots\\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0}
\end{bmatrix}_{n \times m}
$$
在求解線性方程式$\mathbf{Ax} = \mathbf{b}$,其最小平方問題與最小範數問題的通解就是
$$
\text{solve } \mathbf{Ax} = \mathbf{b} \Rightarrow \mathbf{x} = \mathbf{A}^+ \mathbf{b} = (\mathbf{V}\mathbf{\Sigma}^+\mathbf{U}^T) \mathbf{b}
$$
而經過數學推導(省略),可以得出結論 - 最小平方問題、最小範數問題都是用虛反矩陣求解$\mathbf{x} = \mathbf{A}^+ \mathbf{b}$時的特例
給定矩陣$\mathbf{}$
- 最小平方問題 - 如果$m \geq n$且$\mathrm{rank}(\mathbf{A}) = n$,則$\mathbf{A}^+ = (\mathbf{A}^T \mathbf{A})^{-1} \mathbf{A}^T$。
- 最小範數問題 - 如果$m \leq n$且$\mathrm{rank}(\mathbf{A}) = m$,則$\mathbf{A}^+ = \mathbf{A}^T(\mathbf{A} \mathbf{A}^T)^{-1}$。
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet