changed 3 years ago  
Published Linked with GitHub
tags: tutorial

計算幾何＆其他

by FHVirus

閒聊時間

大綱

  • 暖身題
  • 一些基本的運算
  • 凸包
  • 多邊形面積
  • 最遠點對
  • 極角排序（Lawfung Sort）
  • 線段相交
  • 座標轉換
  • 實作時間／一些不相關的題目

小約定

  1. 今天談的東西不是很嚴謹（講者爛）。
  2. 沒有特別指名的話都是在討論二維平面上的事。

暖身

水題大賽？

CF270A

CF1156A

CF1096C

CF195D

Naïve!

一些基本的運算

三角形、多邊形、凸多邊形、直角、面積

大家都會吧？

向量

以下是不嚴謹的簡單的介紹><

想像成箭頭／座標就對了啦ww

我們接下來會用到的東西

  • 大多是二維向量
  • 點積 Dot
  • 叉積 Cross
  • 相加相減（Naïve）

點積（內積）

大概可以描述兩個向量的方向有多一致。
運算方式：\(a \cdot b = a_1 \cdot b_1 + a_2 \cdot b_2 \cdots\)

對於兩個平面的向量：

  • 若方向相同：\(a \cdot b = |a||b|\)
  • 若兩者垂直：\(a \cdot b = 0\)
  • 若方向相反：\(a \cdot b = -|a||b|\)
  • 一般定義：\(a \cdot b = |a||b| \cos \theta\)，其中 \(\theta\) 為兩向量夾角。

叉積（外積）

常用在計算例舉之類的。
注意到，在二維平面的叉積常常直接取數值，
是因為叉積為三維的向量，且 \(a \times b\) 會垂直 \(a, b\)（垂直平面），運算時多當成數值回傳。

計算方式：
對於二維的向量而言，
\(a \times b = a_x \cdot b_y - a_y \cdot b_x\)，
注意這會帶正負號。

手算的話也可以以 \(a \times b = |a||b| \sin \theta\) 計算。

這可以幹嘛？

判斷兩個向量的夾角！

凸包 Convex Hull

別擔心，這裡沒有 DP 優化。

凸包是啥？

「凸」的定義是：圖形內任意兩點的連線不會經過圖形外部。
by 演算法筆記

簡單來說，一群點形成的凸包，就是周長最小且包住所有點的殼！

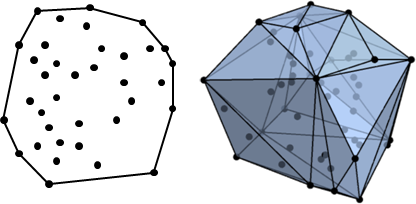
Convex Hull

怎麼做？

掃描、DQ一大堆⋯⋯

都不是今天要教的！

Andrew's Monotone Chain!

上下凸包分開找！

對於所有點按一軸排序，邊掃邊做事！

Andrew's Monotone Chain

要怎麼判斷該不該加點？

還記得叉積嗎？

拿前兩點判斷！

複雜度

  • sort \(O(n \log n)\)
  • 掃描＋Stack 操作 均攤 \(O(n)\)

總複雜度 \(O(n \log n)\)！

例題：TIOJ 1178 Convex Hull

扣的

struct point{
	ll x, y;
	point(){}
	point(ll x, ll y): x(x), y(y){}
	// 不會用到加法就不做了
	point operator-(point p){
		return point(x - p.x, y - p.y);
	}
	// Dot Product
	ll operator*(point p){
		return x * p.x + y * p.y;
	}
	// Cross Product
	// 注意運算子優先度！
	ll operator^(point p){
		return x * p.y - y * p.x;
	}
};

扣的

// All points, lower convex, upper convex
int n;
point p[N], lc[N], uc[N];
int lcp, ucp;

int32_t main(){ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    cin >> n;
    FOR(i,n){
        int a, b; cin >> a >> b;
        p[i] = {a, b};
    }
    sort(p, p + n, [](point a, point b){
        return a.x < b.x;
    });
    FOR(i,n){
        while(ucp > 1 and
            ((p[i] - uc[ucp - 2]) ^ (uc[ucp - 1] - uc[ucp - 2])) >= 0)
            --ucp;
        while(lcp > 1 and
            ((p[i] - lc[lcp - 2]) ^ (lc[lcp - 1] - lc[lcp - 2])) <= 0)
            --lcp;
        uc[ucp++] = p[i];
        lc[lcp++] = p[i];
    }
    // 凸包最左最右會重複算到
    cout << ucp + lcp - 2 << '\n';
    return 0;
}

動態凸包什麼的之後再說

習題：

多邊形面積

大家應該都會算吧？

應該也不少人看過這個：

\[ \begin{align} & \frac{1}{2} \begin{vmatrix} x_1 & x_2 & x_3 & \cdots \\ y_1 & y_2 & y_3 & \cdots \end{vmatrix} \\ = & (x_1 \cdot y_2 - y_1 \cdot x_2) + \cdots + (x_n \cdot y_1 - y_n \cdot x_1) \\ = & v_1 \times v_2 + v_2 \times v_3 + \cdots + v_n \times v_1 \end{align} \]

這東西對於所有多邊形都可以用！
按照逆時針排序點，
順時針的話就取個負號，
複雜度 \(O(n)\)！

就醬，丟題

最遠點對

觀察一下不難發現，
最遠點對一定是凸包上的點對！

怎麼做？

\(O(n^2)\)？

Naïve!

\(O(n)\) ？

建凸包＋雙指針！

我們沿凸包逆時針進行，
對於遇到的每一個點，
其對應到的最遠點也只會逆時針走！

Convex Hull

習題

  • TIOJ 1105 PS3
  • 給定 \(n\) 個點，求其所形成的最大三角形面積（\(n \leq 1500\)）

極角排序＆Lawfung Sort

例題：TIOJ 1205 直角三角形

\(O(n^3)\) ？

Naïve!

\(O(n^2 \log n)\) ？

枚舉每一個點，可以做什麼？

看他是不是直角那個點！

枚舉每個點當直角，
其他的點按照極角排序好，
雙指針掃過去！

（極角：從 x 軸開始逆時針走的夾角）

怎麼照極角排序？

還記得內外積嗎？

Lawfung Sort

小優化 by warner1129

把第三、四象限的點以原點對稱過去！

習題

線段相交

應該是本課最難搞的東西

給你平面上四個點 \(A, B, C, D\)，
求 \(\overline{AB}\) 與 \(\overline{CD}\) 有沒有相交？

重點

  • 有沒有漏 case ？
  • 好好判共線

想想看？

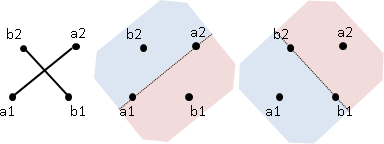
Segment intersection

例題：TIOJ 1876 回家

怎麼判斷一個點在不在簡單多邊形內部？

一個點隨便取一條射線，
若射線交簡單多邊形於奇數個點，
則在多邊形內！

例題：TIOJ 1423 直線線段相交問題 (Intersection)

怎麼做？

亂做！
不要中毒！

座標轉換

很重要

例題：IOI 2007 Pairs

不要被 IOI 嚇到啦w
這題不難？

一維？

還算簡單吧？

二維？

  • 枚舉每一對
  • TLE

從頭想，觀察一下！

提示：平面距離有分三種。
對於兩個點 \(i, j\)，他們的距離：

  • 歐幾里德：\(\sqrt{(x_i - x_j)^2 + (y_i - y_j)^2}\)
  • 曼哈頓（計程車幾何）：\(|x_i - x_j| + |y_i - y_j|\)
  • 切比雪夫：\(\max(|x_i - x_j|, |y_i - y_j|)\)

可以發現，如果題目要求的是切比雪夫的話，就可以用區間資料結構掃過去！

但是，要怎麼做？

展開過程，
如果你上課的時候還看到這邊，
代表 FHVirus 沒做完講義，
她會負責現場導一次的。

這個技巧在二維可以把曼哈頓轉成切比雪夫！

三維也用一樣的技巧，
只不過你的式子會有四個維度！

\(\color{green}{AC}\)

恭喜你會一題 IOI 囉！

為什麼很重要？

實作時間／雜題大戰

ARC113 D

Select a repo